清明 DAY 3

ans=1000*4

分别固定千位，百位，十位，个位为1，其余位置随便排

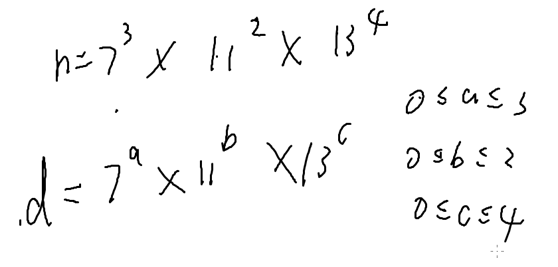
对于每一个质因数的n次方，共有n+1中选择方法，即这个质因数的0~n次方

故共有   4*3*5=60  种方法

(1)取两册文字不同的书的方案=取日文英文+取日文中文+取英文中文

5*7+5*10+7*10

(2)相同的：取日文日文，取中文中文，取英文英文

5*4/2+7*6/2+10*9/2

(3)     (1)+(2)

PS：高中课本上写的是 A（然鹅这并不对） 而不是 P

考虑两面旗帜的方法和三盆花的方法，根据乘法原理乘起来即可

ans=P(5,2)*P(20,3)

先考虑对七名男生排序，然后在六个间隔中插入三名女生

ans=P(7,7)*P(6,3)

ans = 7*8*(4+5+4+5+4) = P(8,2)*22

正难则反

总的方案数减去选上男A和女B的方案数

ans=C(12,5)-C(10,3)

按余数分类：余数相同和余数不同

余数相同分为：(0,0,0),(1,1,1).(2,2,2);

1~300这些数中，余数相同的各有100个

故每一种可能的方式均为C(100,3)

余数不同时，每一个数都是从不同的余数中选一个，故方式为C(100,1)³

ans=3*C(100,3)+C(100,1)³

由于每种颜色的旗帜是相同的，所以讲相同颜色的旗帜放一起，只能算是一种方式

这个时候我们需要用组合数

ans=C(16,4)*C(12,4)*C(8,4)*C(4,4)

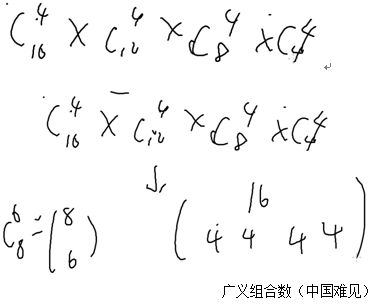
• 有n个不同元素，从中选r个，但是每个可以选多次，则其方案数为C(n+r-1,r)

证：设选的数为a1,a2,....,ar，（由小到大），则1≤a₁≤a₂≤a₃......≤a_r≤n

我们可以通过一种变换，就是让ai+i-1，这样可以去掉=

有：1≤a₁<a₂+1<a₃+2<.....<a_r+r-1<n-r+1

中间还是有r个数，我们可以设b_i=a_i+i-1

则1≤b₁<b₂<b₃<....<b_r≤n-r+1

所以问题就开始转换为无重复组合问题，即在n+r-1 个元素中选中 r个的组合数 。

（简而言之就是每一个数字都可以在 n 个当中选，也可以在 r-1 个当中选）

• 有n个不同元素，从中选r个，但是选中的元素大小不能相邻，则其方案数为C(n-r+1,r)

证：设选的数为a1,a2,....,ar，（由小到大），则1<a₁<a₂<a₃<......<a_r<n

其中a₁+1<a₂，a₂+1<a₃....

将每个a_i-i+1

有a₁<a₂-1<a₃-2<...<a_r-r+1

      

      其他的一些性质

• Cⁿ_n+m = C^m_n+m

 

• C ^m_n = C ^m-1_n-1+C ^m_n-1 

                        //组合数 递推式  第一个东西选C（n-1，m-1）或者不选C（n-1，m）

• C ^r_n+r+1 = C ^r_n+r + C ^r-1_n+r-1 + C ^r-2_n+r-2 +....+C⁰_n

//运用第二行不断拆

• C ^l_n C ^r_l = C ^r_n C ^l-r_n-r

//打标机，打两次

• C⁰_n +C¹_n +.....+Cⁿ_n =2ⁿ

//从n 个东西里选任意东西的方案数（左式），每个数都可以选或不选（右式）

• C⁰_n - C¹_n +C²_n - ... = 0

//选奇数个方案数=选偶数个方案数

奇数方案数 >= 偶数方案数  偶数方案数 >= 奇数方案数

奇数方案数第一个东西不选，那就变为选偶数个的方案数

杨辉三角里奇数列的和=偶数列的和

• C ^r_r + C^r_r+1 +...+ C ^r_n =C^r+1_n+1

先来看一道题

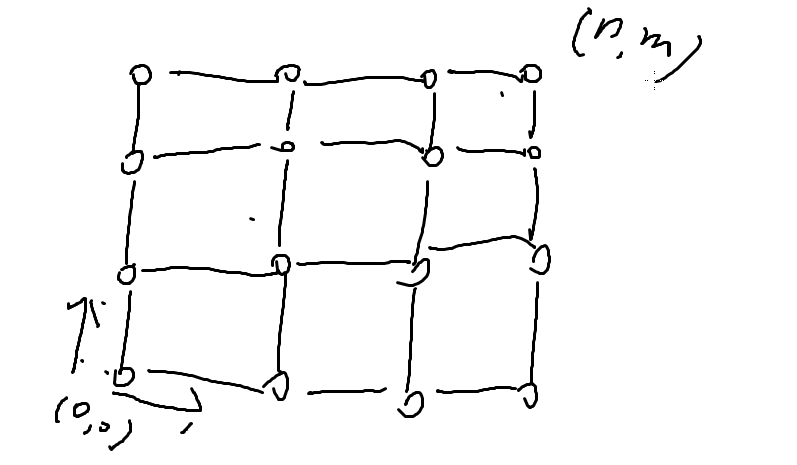
如图，一个n*m的方格中，从原点开始，每次只能向上走或者向右走，求走到点(n,m)共有多少种走法

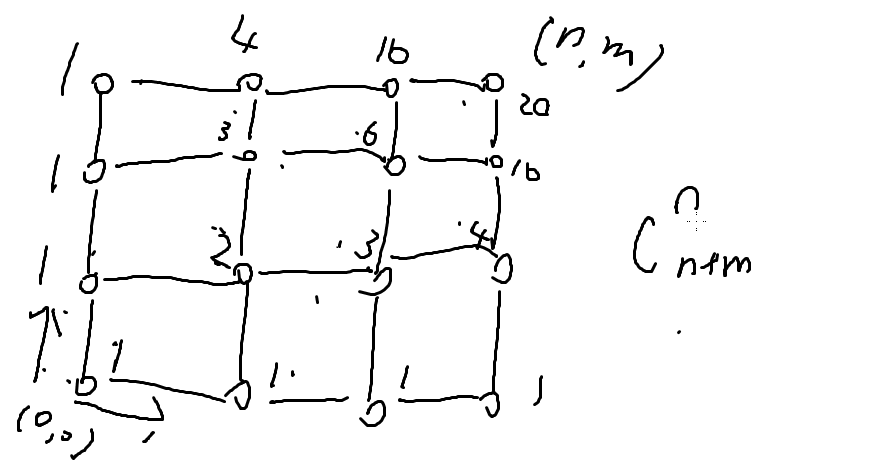
（ 斜着看      你发现了一个杨辉三角 ）

一般做法：

一个一个写，每一个节点的种数=它左边的数量+右边的数量

组合数：  ans=C(n+m,n)

原因：一共要走n+m步，从中选出n步向右走的，即为答案（C(n+m,m) 一样）

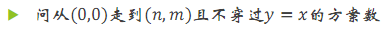
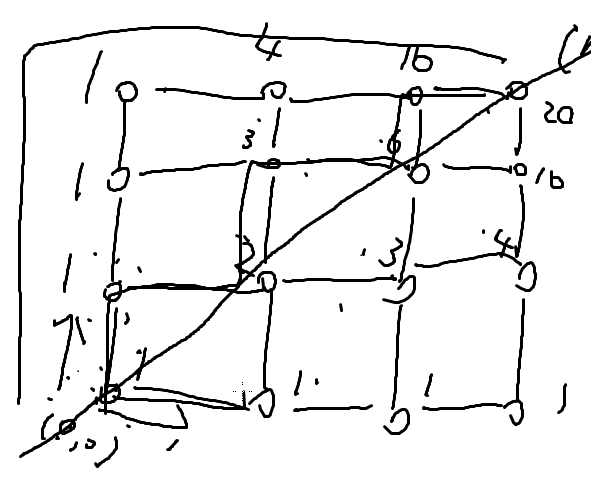
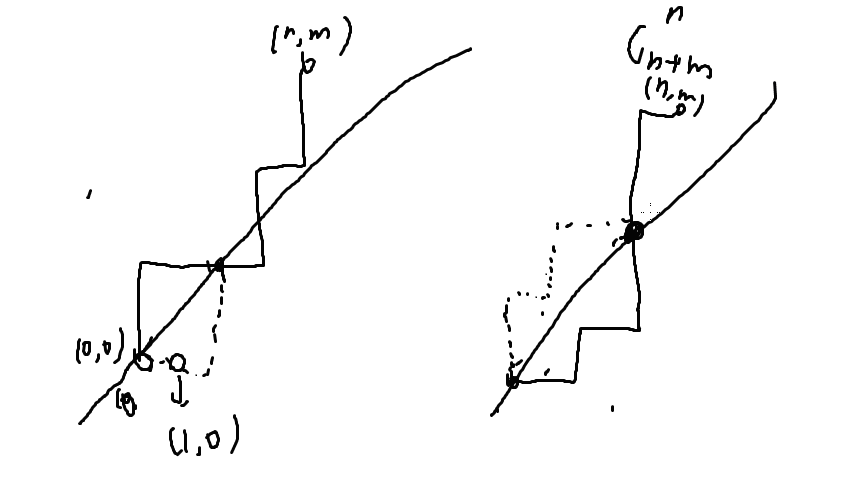
一个不合法方案一定经过（1，0）,（n,m）

不合法的方案经过（1，0），那么他一定会和y=x相交

每个非法方案都对应一个从（1，0）到（n,m）方案

so,    ans = Cⁿ_n+m – C^n-1_n-m-1

Luogu 4369

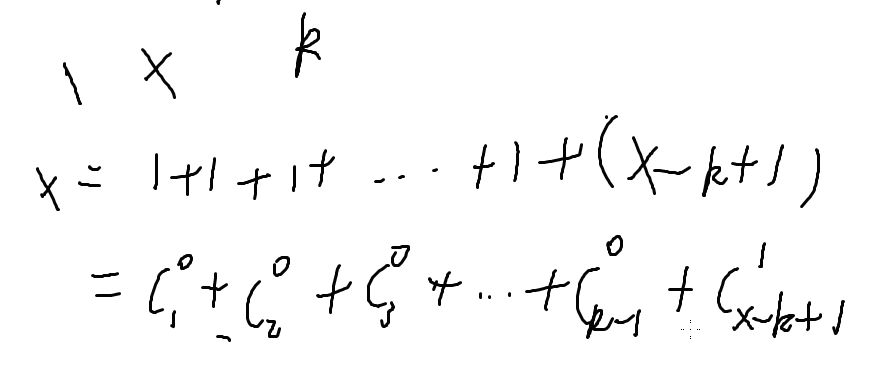
任意一个数都可拆成k个1

也就是k-1个1和一个x-k+1

（底数大于1）

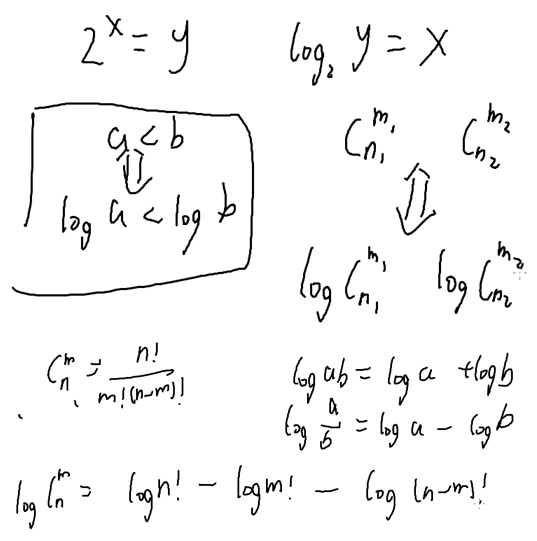
维护n！前缀和 ，比较log

O（n）复杂度

Problem2+加上一个堆
         Luogu 4370

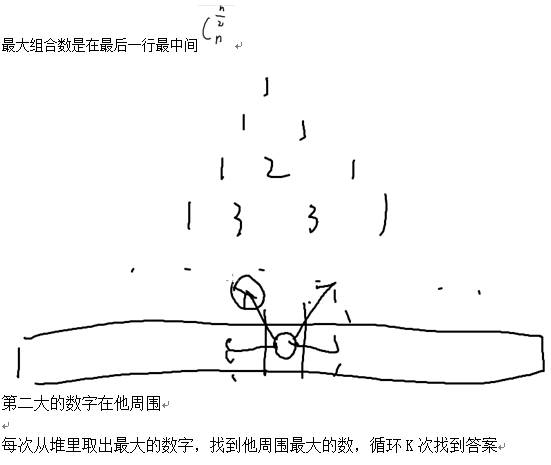
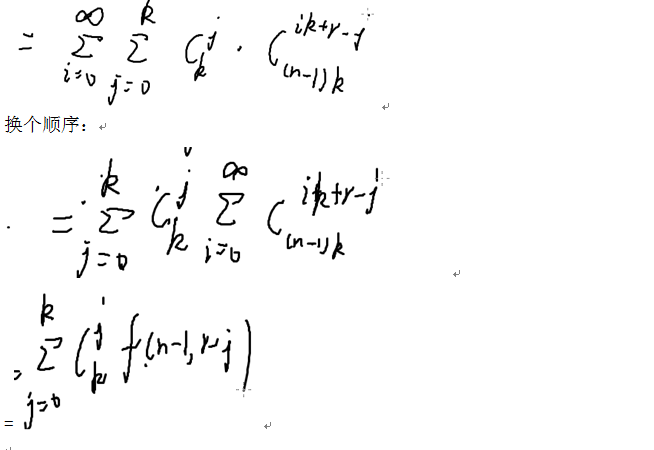
结合转移矩阵

Luogu 3746

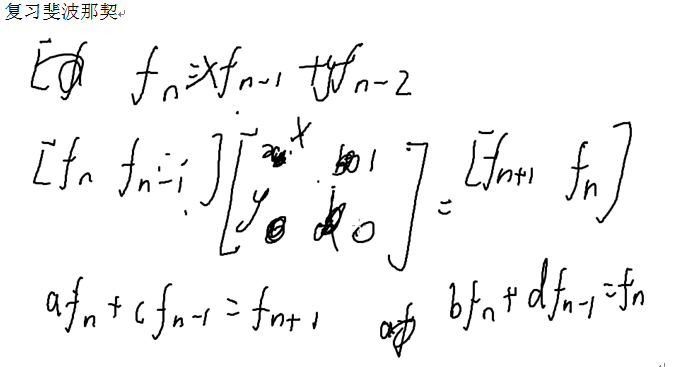
 数位dp
 Bzoj 4737

题解一

P2822 组合数问题

题解二

Lucas定理

P为素数，则有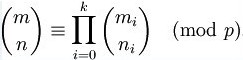

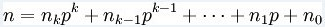
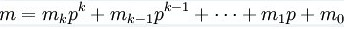
Just like this：

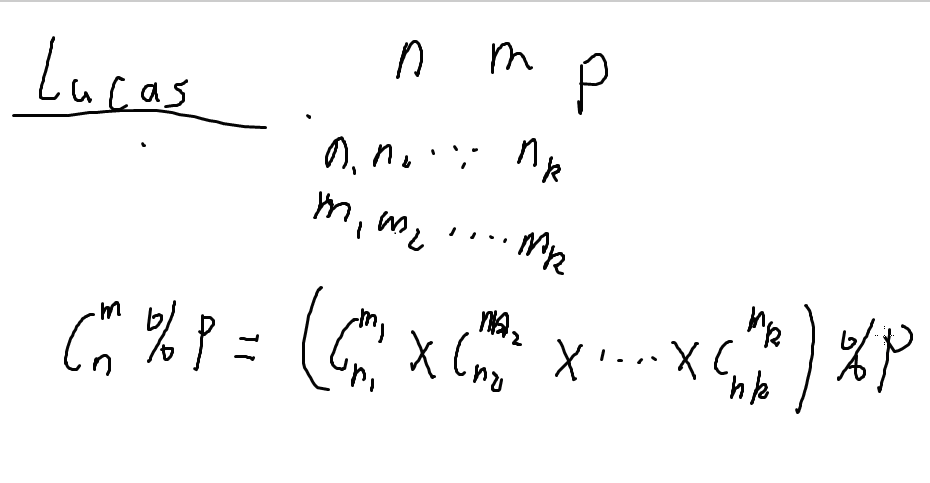
注：这里是将n，m转化为p进制

因为C(n,m)是p的倍数，而C(ni,mi)中并不含有p，所以某一位有ni<mi使得它=0

 根据维恩图    170+130+120-45-20-22+3

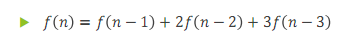
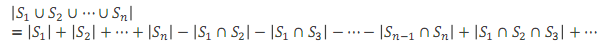
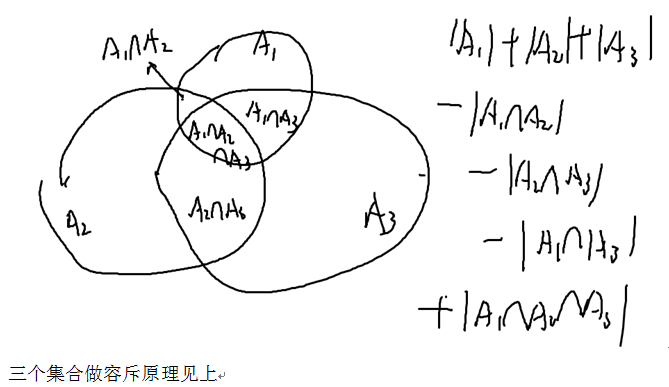
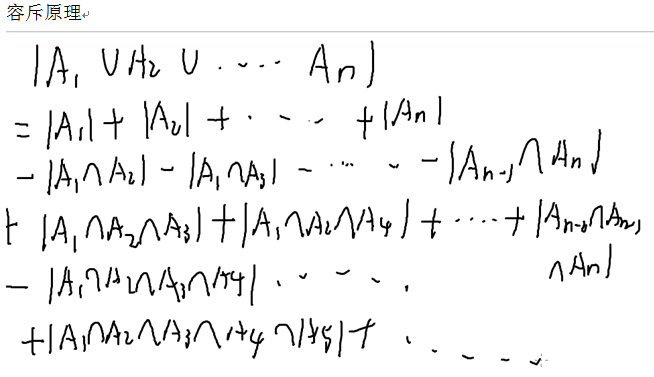
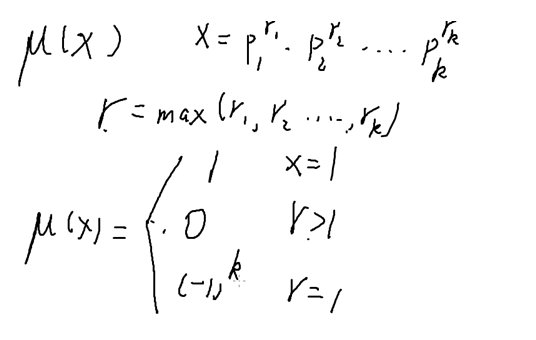
（这题走错地了吧   直接算就行）

随便送：P（6，6）

不合法：C(6,1) * P(5,5)

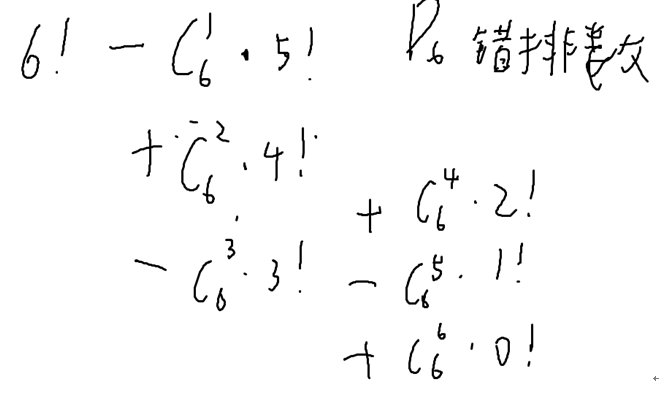
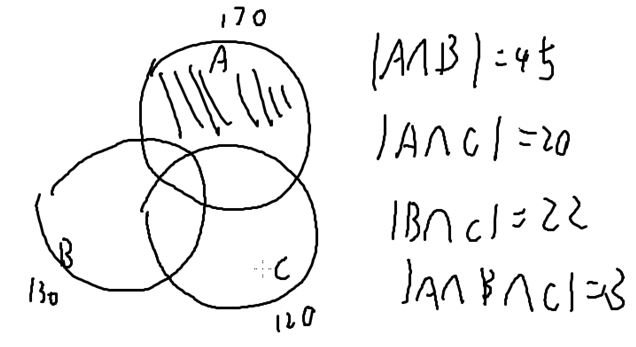
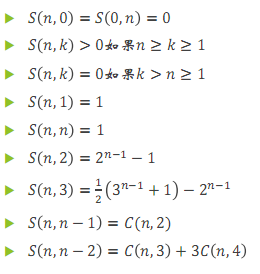
总结一下就是：

 

不能打羽毛球的情况有：

球  >=0      >=1      =0       

拍   =0       =1        > =1 

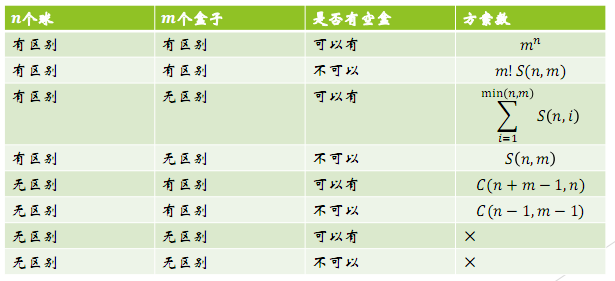
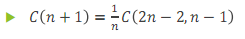
然后二者结合

---

特别鸣谢：ych