树链剖分&咕咕咕了好久好久的qtree3

前言

显然qtree系列都是树链剖分辣

发现自己没有专门整理过树链剖分耶

辣么就把这篇博客魔改成树链剖分好辣（貌似除了树剖也没什么好写的）

正文

废话了辣么多终于开始了

一.树剖怎么写鸭

二.树剖有什么用鸭

三.qtree3题解

树剖怎么写鸭

树剖，顾名思义就是把树 剖成一条一条的东西，然后把一棵树搞成一个序列。
咋剖？
对于树上的每个节点，我们定义它的儿子中，有着最大子树的儿子就是重儿子（因为它画出来显得比较重），然后我们从根节点开始，一直走重儿子，就走出来一条重链。那些不在重链上的边怎么办呢？我们给他们起个名字，叫轻边。

处理重儿子

void dfs1(int u,int fa)
{
	dep[u]=dep[fa]+1;//这是深度
	par[u]=fa;
	sz[u]=1;
	for(int e=head[u];e;e=ed[e].nxt)
	{
		int v=ed[e].to;
		if(to==fa)continue;
		dfs(v,u);
		sz[u]+=sz[v];
		if(sz[son[now]]<sz[v])son[now]=v;
	}
	return;
}

我们要把树搞成一个序列，所以要给每个节点一个编号dfn。dfn就是dfs序，dfn[i]也就是节点i是在dfs时第几个被遍历到了。在dfs时，先走重儿子，再走其他儿子。这样所有重儿子的dfn就是连续的，方便后面进行操作（why?）

emm蒟个栗子



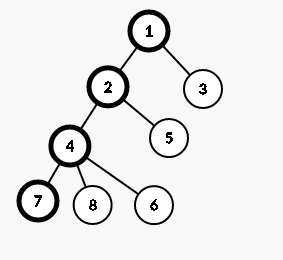
其中加粗的点构成一条重链（最下面的点也可以是8,9）

搞重链和轻边

void dfs2(int u,int fa)
{
	cnt++;
	dfn[u]=cnt;
	id[cnt]=u;//记录dfn值对应的原来的编号
	if(son[fa]==u)top[u]=top[fa];
	else top[u]=u;
	if(!son[u])return ;
	dfs2(son[u],u);
	for(int e=head[u];e;e=ed[e].nxt)
	{
		int v=ed[e].to;
		if(v!=fa&&v!=son[u])
		 dfs2(v,u);
	}
}

辣么我们搞这个重链到底有什么用呢

良(du)心(liu)出题人肯定会搞一些树上的询问对不对？树上的询问一般都要涉及两个点之间的路径对不对？要搞路径就要找lca对不对？这时候就要用到重链和轻边了。

对于每一条链都会有一个链的顶部（一条轻边自己就是一条链），我们可以一条链一条链的往上跳，也就是每次都跳到当前所在链的顶部再往上一个点（以便找下一个顶部）。这样，当再跳一步，两个点所在链的顶部相同时，就说明lca在这条链中。

再蒟个栗子



现在我们要求6和8的lca

图中加粗的点是重儿子

6所处的链的顶端是1,8的顶端是10

这里我们先跳顶端比较深的那个点，也就是跳8

如果跳这一步：



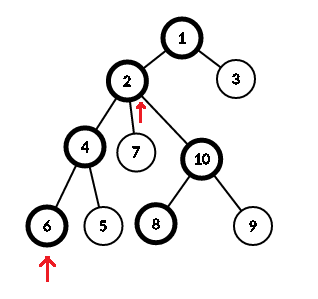
这时候发现2和6的顶端是一样的，说明6和8的lca肯定在1->2->4->6这条链中

那么2和6中靠近根的点就是lca,在这里就是2。

找到了lca之后呢？再从lca往下跑？

不，不需要这么麻烦。

我们在上面处理dfn的时候，处于同一条重链上的点的dfn是连续的，也就是构成了一个区间。这个区间里的信息可以在线段树上维护。所以我们在找lca的时候，同时将这段区间的信息统计到答案里面。所以我们就切掉了查询操作。

查询代码(以求点权之和为例)

int sum(int x,int y)
{
	int ans=0;
	while(top[x]^top[y])//top[x]!=top[y]
	{
		if(dep[top[x]]<dep[top[y]])swap(x,y);
		ans+=query(1,1,n,dfn[top[x]],dfn[x]);//query就是线段树的query辣
		x=par[top[x]];
	}
	if(dep[x]>dep[y])swap(x,y);
	 ans+=query(1,1,n,dfn[x],dfn[y]);
	return ans;
}

什么？线段树怎么写？点这里qwq至于线段树维护什么因题而异，这里就不多说辣。

树剖是个什么玩意&有什么用

树剖可以对树进行操作，然后把树搞成一个区间，再加上线段树等数据结构的辅助，从而让我们的暴力跑的更快（港真树链剖分其实是一个优化暴力）

经典类型（可能以后会补充）：原本序列上的操作被duliu出题人搞到了树上；给出的图是一棵树而且还会神烦的改边权

qtree3的题解

[传送](https://www.luogu.org/problem/P4116)

其实qtree系列的难点在于我们要在线段树上维护什么。

对于这道题，我们要在线段树上维护什么呢？

当然是当前节点代表的区间中第一个黑点的dfn值辣。（初始值全部为inf）

然后结合线段树和树剖的板子这道题就写完了

一个大小坑:

我们在树剖的时候建的是双向边，所以注意#####数组要开到2e5!!!!!

鉴于luogu是个神奇的网站，不开2e5的边的评测结果是这样的：

emmmm当时真的以为是query无限递归什么的然后愣是WA了一个月没调出来,某天吃饭的时候突然醒悟边tm开小了

Code:

#include<iostream>
#include<queue>
#include<cstdio>
#include<algorithm>
#include<cstring>
#include<cmath>
#define pa pair<int,int>
typedef long long ll;
using namespace std;
inline int read()
{
    char ch=getchar();
    int x=0;bool f=0;
    while(ch<'0'||ch>'9')
    {
        if(ch=='-')f=1;
        ch=getchar();
    }
    while(ch>='0'&&ch<='9')
    {
        x=(x<<3)+(x<<1)+(ch^48);
        ch=getchar();
    }
    return f?-x:x;
}
const int inf=21474836;
int fir[300009],dfn[100009],son[100009],par[100009],top[100009];
int n,q,dep[100009],cnt,head[100009],sz[100009];
int tim,idx[100009];
struct E{
    int to,nxt;
}ed[300009];
void add(int fr,int to)
{
    cnt++;
    ed[cnt].to=to;
    ed[cnt].nxt=head[fr];
    head[fr]=cnt;
}
void dfs1(int now,int fa)
{
    dep[now]=dep[fa]+1;
    par[now]=fa;
    sz[now]=1;
    for(int e=head[now];e;e=ed[e].nxt)
    {
        int v=ed[e].to;
        if(v==fa)continue;
        dfs1(v,now);
        sz[now]+=sz[v];
        if(sz[v]>sz[son[now]])
         son[now]=v;
    }
    return ;
}
void dfs2(int now,int fa)
{
    ++tim;
    dfn[now]=tim;
    idx[tim]=now;
    if(son[fa]==now)
     top[now]=top[fa];
    else top[now]=now;
    if(!son[now]) return;
	dfs2(son[now],now);
    for(int e=head[now];e;e=ed[e].nxt)
    {
        int v=ed[e].to;
        if(v!=son[now]&&v!=fa)
         dfs2(v,now);
    }
//  printf("dfn[%d]=%d\n",now,dfn[now]);
}
void build(int k,int l,int r)
{
    if(l==r)
    {
        fir[k]=inf;
        return ;
    }
    int mid=(l+r)>>1;
    build(k<<1,l,mid);
    build(k<<1|1,mid+1,r);
    fir[k]=inf;
}
void chg(int k,int l,int r,const int &v)
{
    if(l==r)
    {
        if(fir[k]==inf) fir[k]=l;
        else fir[k]=inf;
        return ;
    }
    int mid=(l+r)>>1;
    if(v<=mid) chg(k<<1,l,mid,v);
    else chg(k<<1|1,mid+1,r,v);
    fir[k]=min(fir[k<<1],fir[k<<1|1]);
}
int query(int k,int l,int r,const int &x,const int &y)
{
    if(x<=l&&r<=y)
    {
        return fir[k];
    }
    int mid=(l+r)>>1;
    int rtn=inf;
    if(x<=mid) rtn=min(rtn,query(k<<1,l,mid,x,y));
    if(mid<y) rtn=min(rtn,query(k<<1|1,mid+1,r,x,y));
    return rtn;
}
int qfir(int x)
{
    int y=1;
    int rtn=inf;
    while(top[y]^top[x])
    {
        if(dep[top[x]]<dep[top[y]])swap(x,y);
        rtn=min(rtn,query(1,1,n,dfn[top[x]],dfn[x]));
        x=par[top[x]];
    }
    if(dep[x]>dep[y])swap(x,y);
    rtn=min(rtn,query(1,1,n,dfn[x],dfn[y]));
    return rtn;
}
int main()
{
    n=read();q=read();
    for(int i=1;i<n;i++)
    {
        int fr=read(),to=read();
        add(fr,to);
        add(to,fr);
    }
    dfs1(1,0);
    dfs2(1,0);
    build(1,1,n);
    for(int i=1;i<=q;i++)
    {
        int cz=read(),v=read();
        if(cz==0)
         chg(1,1,n,dfn[v]);
        else
        {
            int ans=qfir(v);
            printf("%d\n",((ans==inf)?-1:idx[ans]));
        }
    }
}

好了在结尾安利一道树剖模板题