机器人自主移动的秘密：实际应用中，SLAM究竟是如何实现的？（二）

博客转载自：https://www.leiphone.com/news/201612/FRzmoEI8Iud6CmT2.html

雷锋网(公众号：雷锋网)按：本文作者SLAMTEC（思岚科技公号slamtec-sh）技术顾问，专注SLAM及相关传感器研发应用。

SLAM主要解决机器人的实时定位与自动建图问题，那么，在实际应用时，SLAM究竟是如何实现的呢？在实现过程中有哪些难点？这是一个完整的SLAM和导航系统的主要架构图：

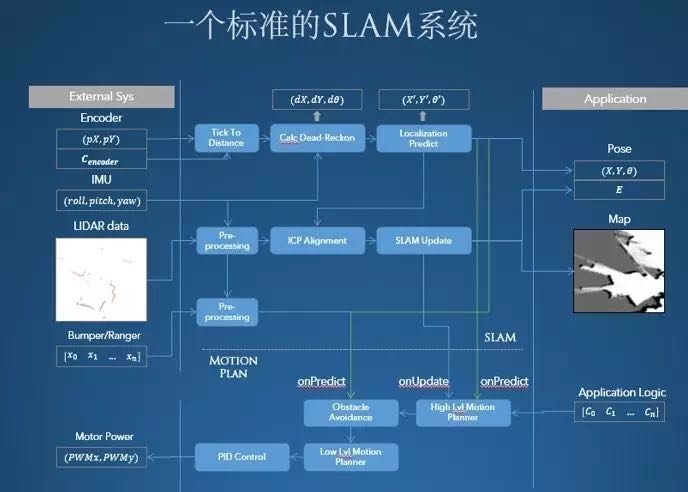
其中，SLAM核心过程包括3个步骤，第一步称为预处理。

我们知道，激光雷达和其他雷达设备一样，某一个时刻只能获取它所在位置的环境信息。这就是我们所说的点云，它只能反映机器人所在环境中的一个部分。第一步预处理就是对激光雷达原始数据进行优化，剔除一些有问题的数据，或者进行滤波。

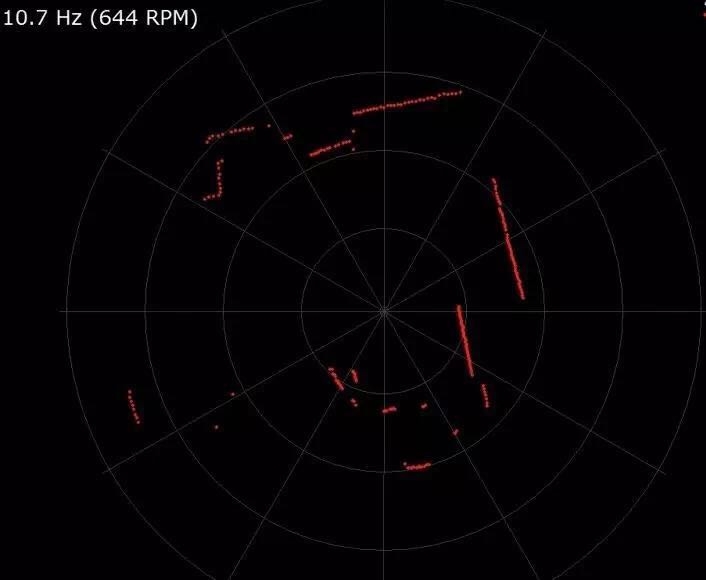
第二步是匹配，也就是说把当前这一个局部环境的点云数据在已经建立地图上寻找到对应的位置，这个步骤非常关键。

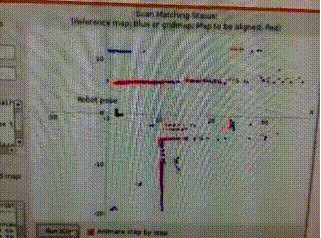
这个是ICP的点云匹配算法，用于实现匹配。说这个过程关键，就是因为它的好坏，直接影响了SLAM构建地图的精度。这个过程和我们玩拼图游戏有点类似，就是在已经拼好的画面中找到相似之处，确定新的一个拼图该放在哪里。

在SLAM过程中，需要将激光雷达当前采集的点云（红色部分）匹配拼接到原有地图中。

如果不进行匹配过程，所构建的地图可能就乱成一团，变成这样。

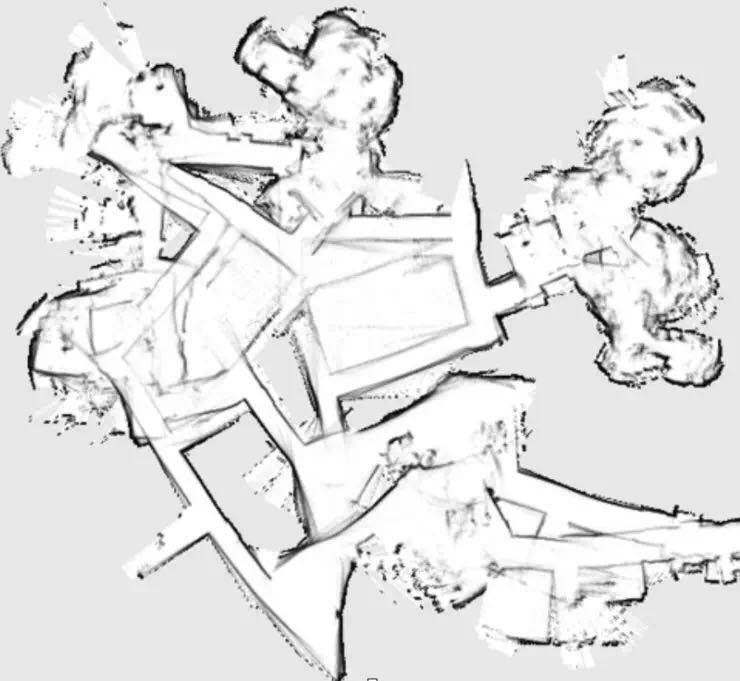
在这个部分完毕以后，就进行第三步，地图融合，也就是将这一轮来自激光雷达的新数据拼接到原始地图当中，最终完成地图的更新。就像这个图一样，这个过程是永远伴随SLAM过程的。

数据融合和简单的贴图是有很大的差异的。因为实际上传感器描绘的世界存在一定的误差，或者正巧在这个时间环境有了变化，例如机器人旁边闯入了一只小猫。因此，实际要进行的过程会更加复杂，需要用很多概率算法，并采用滤波的方式进行融合。将上述这个过程逐次执行，就最终产生了我们看到的栅格地图。

这个过程听起来其实并不复杂，但是要处理好有很大难度。这里举几个例子，比如叫做Loop Closure（回环）问题。如果匹配算法不足够优秀，或者环境中存在很不巧的干扰，当机器人绕着环境一圈后，就会发现原本是应该闭合的一个环形走廊断开了。

比如正常地图应该这样：

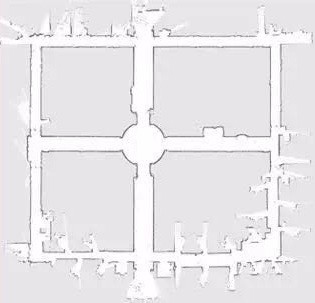
如果处理不好，实际地图就成这样：

对于环境比较大的场景，回环问题是不得不面对的，但现实总是不完美的，即使是激光雷达这种高精度传感器，也难免存在误差。而回环问题的难点恰恰在于在一开始出现少许误差的时候，并不会被发觉，直到机器人绕着环路一圈，随着误差的累加，发现环路已经无法闭合时，此时已经酿成大错，一般很难回天。当然这个问题并不是无解，一个好的商用化SLAM系统，回环问题是否能很好的解决，就成为评判这个系统实力的指标了。

这是前两天在我们办公室进行的测试，左边的视频是基于开源的ROS机器人操作系统进行的地图构建，右边的是基于SLAMWARE构建的地图。当机器人已经绕场一周后，ROS构建的地图出现了中断，而SLAMWARE构建的地图是一个完美的闭环，它与我们办公室的设计图完美重合。

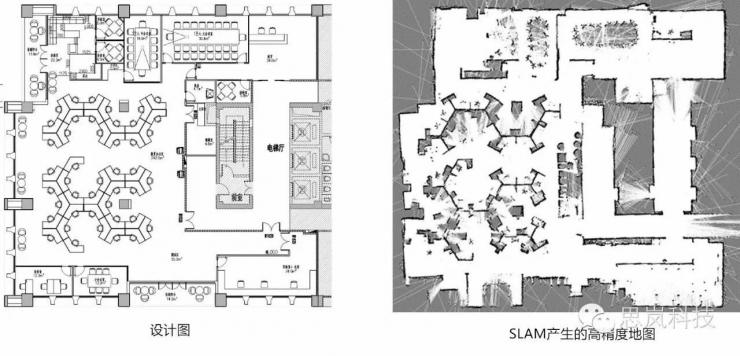
除了算法层面的回环问题，SLAM实际应用中还有很多这种坑，比如走廊问题与外界干扰问题。

以外界干扰问题来说，通常，激光雷达作为机器人的眼睛，一般是安装在底盘上的，它能看到的视野很有限。当受到外界干扰（人类或者宠物等等）后，机器人很容易丢失定位精度，无法正常完成后续的建图工作。

当机器人安装SLAMWARE后，机器人受到干扰，可以完全不受影响，照样能够正常工作。

视频请查看原博客

目前，SLAM的开源实现代表多为学术界，实际应用有很多Corner Case要处理，需要传感器、系统参数、其他辅助设备的联合调优。

一般来说，上述的SLAM过程对于运算消耗是巨大的，虽然并没有达到像训练神经网络动用服务器集群那种地步，但传统上需要PC级别的处理器。

除配备激光雷达外，还需要机器人具有IMU（惯性测量单元）、里程计来为激光雷达提供辅助数据，否则SLAM系统也难以得到运行。总的来说，SLAM算法本身是一个对于外部系统有着多种依赖的算法，这是一个切实的工程问题。很多机器人，比如扫地机是不可能装一个PC进去的，为了让SLAM能在这类设备里运行，除了解决激光雷达成本外，还要对SLAM算法做出很好的优化。

这也是我们思岚科技SLAMTEC主要的努力方向，一方面，我们这7年多很好的解决了各类实际SLAM算法难点，另一方面，我们把SLAM这个复杂的系统做了很大的优化，可以放到一个硬币那么大的模块内部，降低尺寸功耗。此外，它还集成了IMU等配套传感器，力求做到对于SLAM的使用便捷性。

那么，机器人利用SLAM技术得到了有效的空间信息后，它是怎样实现路径规划的？SLAM和路径规划之间关系是怎样的？下一篇文章，雷锋网将持续更新，如有兴趣可持续关注。

本文转自雷锋网，如需转载请至雷锋网官网申请授权。