Prim 最小生成树算法

Prim 算法是一种解决最小生成树问题（Minimum Spanning Tree）的算法。和 Kruskal 算法类似，Prim 算法的设计也是基于贪心算法（Greedy algorithm）。

Prim 算法的思想很简单，一棵生成树必须连接所有的顶点，而要保持最小权重则每次选择邻接的边时要选择较小权重的边。Prim 算法看起来非常类似于单源最短路径 Dijkstra 算法，从源点出发，寻找当前的最短路径，每次比较当前可达邻接顶点中最小的一个边加入到生成树中。

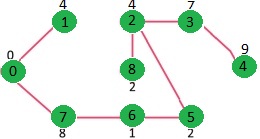
例如，下面这张连通的无向图 G，包含 9 个顶点和 14 条边，所以期待的最小生成树应包含 (9 - 1) = 8 条边。

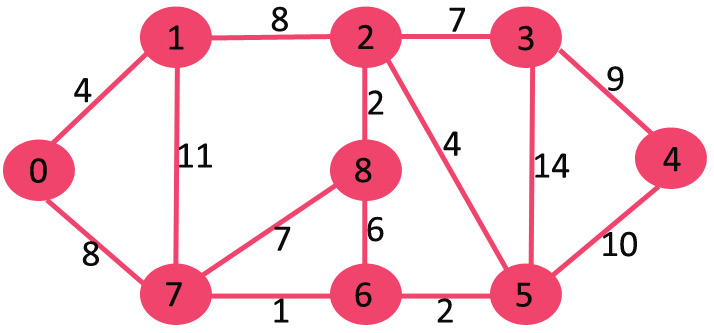
创建 mstSet 包含到所有顶点的距离，初始为 INF，源点 0 的距离为 0，{0, INF, INF, INF, INF, INF, INF, INF, INF}。

选择当前最短距离的顶点，即还是顶点 0，将 0 加入 MST，此时邻接顶点为 1 和 7。

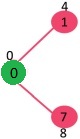
选择当前最小距离的顶点 1，将 1 加入 MST，此时邻接顶点为 2。

选择 2 和 7 中最小距离的顶点为 7，将 7 加入 MST，此时邻接顶点为 6 和 8。

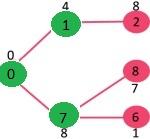
选择 2, 6, 8 中最小距离的顶点为 6，将 6 加入 MST，此时邻接顶点为 5。

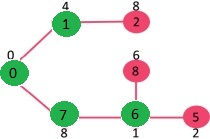
重复上面步骤直到遍历完所有顶点为止，会得到如下 MST。

C# 实现 Prim 算法如下。Prim 算法可以达到 O(ElogV) 的运行时间，如果采用斐波那契堆实现，运行时间可以减少到 O(E + VlogV)，如果 V 远小于 E 的话，将是对算法较大的改进。

 using System;
 using System.Collections.Generic;
 using System.Linq;

 namespace GraphAlgorithmTesting
 {
   class Program
   {
     static void Main(string[] args)
     {
       Graph g = new Graph();
       g.AddEdge(, , );
       g.AddEdge(, , );
       g.AddEdge(, , );
       g.AddEdge(, , );
       g.AddEdge(, , );
       g.AddEdge(, , );
       g.AddEdge(, , );
       g.AddEdge(, , );
       g.AddEdge(, , );
       g.AddEdge(, , );
       g.AddEdge(, , );
       g.AddEdge(, , );
       g.AddEdge(, , );
       g.AddEdge(, , );

       // sorry, this is an undirect graph,
       // so, you know that this is not a good idea.
       List<Edge> edges = g.Edges
         .Select(e => new Edge(e.End, e.Begin, e.Weight))
         .ToList();
       foreach (var edge in edges)
       {
         g.AddEdge(edge.Begin, edge.End, edge.Weight);
       }

       Console.WriteLine();
       Console.WriteLine("Graph Vertex Count : {0}", g.VertexCount);
       Console.WriteLine("Graph Edge Count : {0}", g.EdgeCount);
       Console.WriteLine();

       List<Edge> mst = g.Prim();
       Console.WriteLine("MST Edges:");
       foreach (var edge in mst.OrderBy(e => e.Weight))
       {
         Console.WriteLine("\t{0}", edge);
       }

       Console.ReadKey();
     }

     class Edge
     {
       public Edge(int begin, int end, int weight)
       {
         this.Begin = begin;
         this.End = end;
         this.Weight = weight;
       }

       public int Begin { get; private set; }
       public int End { get; private set; }
       public int Weight { get; private set; }

       public override string ToString()
       {
         return string.Format(
           "Begin[{0}], End[{1}], Weight[{2}]",
           Begin, End, Weight);
       }
     }

     class Graph
     {
       private Dictionary<int, List<Edge>> _adjacentEdges
         = new Dictionary<int, List<Edge>>();

       public Graph(int vertexCount)
       {
         this.VertexCount = vertexCount;
       }

       public int VertexCount { get; private set; }

       public IEnumerable<int> Vertices { get { return _adjacentEdges.Keys; } }

       public IEnumerable<Edge> Edges
       {
         get { return _adjacentEdges.Values.SelectMany(e => e); }
       }

       public int EdgeCount { get { return this.Edges.Count(); } }

       public void AddEdge(int begin, int end, int weight)
       {
         if (!_adjacentEdges.ContainsKey(begin))
         {
           var edges = new List<Edge>();
           _adjacentEdges.Add(begin, edges);
         }

         _adjacentEdges[begin].Add(new Edge(begin, end, weight));
       }

       public List<Edge> Prim()
       {
         // Array to store constructed MST
         int[] parent = new int[VertexCount];

         // Key values used to pick minimum weight edge in cut
         int[] keySet = new int[VertexCount];

         // To represent set of vertices not yet included in MST
         bool[] mstSet = new bool[VertexCount];

         // Initialize all keys as INFINITE
         for (int i = ; i < VertexCount; i++)
         {
           keySet[i] = int.MaxValue;
           mstSet[i] = false;
         }

         // Always include first 1st vertex in MST.
         // Make key 0 so that this vertex is picked as first vertex
         keySet[] = ;
         parent[] = -; // First node is always root of MST 

         // The MST will have V vertices
         for (int i = ; i < VertexCount - ; i++)
         {
           // Pick thd minimum key vertex from the set of vertices
           // not yet included in MST
           int u = CalculateMinDistance(keySet, mstSet);

           // Add the picked vertex to the MST Set
           mstSet[u] = true;

           // Update key value and parent index of the adjacent vertices of
           // the picked vertex. Consider only those vertices which are not yet
           // included in MST
           for (int v = ; v < VertexCount; v++)
           {
             // graph[u, v] is non zero only for adjacent vertices of m
             // mstSet[v] is false for vertices not yet included in MST
             // Update the key only if graph[u, v] is smaller than key[v]
             if (!mstSet[v]
               && _adjacentEdges.ContainsKey(u)
               && _adjacentEdges[u].Exists(e => e.End == v))
             {
               int d = _adjacentEdges[u].Single(e => e.End == v).Weight;
               if (d < keySet[v])
               {
                 keySet[v] = d;
                 parent[v] = u;
               }
             }
           }
         }

         // get all MST edges
         List<Edge> mst = new List<Edge>();
         for (int i = ; i < VertexCount; i++)
           mst.Add(_adjacentEdges[parent[i]].Single(e => e.End == i));

         return mst;
       }

       private int CalculateMinDistance(int[] keySet, bool[] mstSet)
       {
         int minDistance = int.MaxValue;
         int minDistanceIndex = -;

         for (int v = ; v < VertexCount; v++)
         {
           if (!mstSet[v] && keySet[v] <= minDistance)
           {
             minDistance = keySet[v];
             minDistanceIndex = v;
           }
         }

         return minDistanceIndex;
       }
     }
   }
 }

输出结果如下：

参考资料

• Connectivity in a directed graph
• Strongly Connected Components
• Tarjan's Algorithm to find Strongly Connected Components

本篇文章《Prim 最小生成树算法》由 Dennis Gao 发表自博客园，未经作者本人同意禁止任何形式的转载，任何自动或人为的爬虫转载行为均为耍流氓。