栈和队列&前缀，中缀，后缀

1.堆和栈的区别？

　　（1）栈内存操作系统来分配，堆内存由程序员自己来分配。

　　（2）栈有系统自动分配，只要栈 剩余空间大于所申请空间，系统将为程序提供内存，否则将报异常提示栈溢出。

2.栈（线性表）

　　仅限于在栈顶进行插入和删除操作。

　　一般用top变量来指示栈顶元素在数组中的位置。top=0，表示栈中存在一个元素。top=-1，表示空栈。这样就是栈底层实现是数组（类似于线性表的顺序存储）

　　也可以用链式存储，叫做栈的链式存储，链栈

　　进栈操作：（假设新结点是s）

　　　　　　　s->next=S->top;//把当前（S->top）的栈顶元素赋值给新元素的直接后继（s->next）

　　　　　　　S->top=s;//把新的结点s赋值给栈顶指针

　　出栈操作：（假设p用来存储要删除的栈顶结点）

　　　　　　　　p=S->top;//把栈顶结点赋值给p

　　　　　　　　S->top=S->top>next;//使得栈顶指针下移一位，指向后一结点。

　　栗子1：若一序列进栈顺序为e1,e2,e3,e4,e5,问存在多少种可能的出栈序列（）

　　　　　　f(n) = f(0)*f(n-1) + f(1)*f(n-2) + ... + f(n-1)*f(0)，其中f(0)=1，f(1)=1，f(2)=2，f(3)=5

　　　　　　f(5)=f(0)*f(4)+ f(1)*f(3) + f(2)*f(2) + f(3)*f(1) + f(4)*f(1) =42

　　　

　

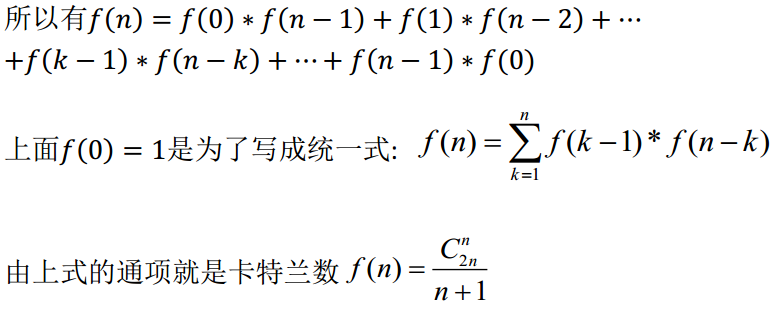
　　栗子2：

　　若栈采用链式存储结构，则：

　　不需要判断栈满但需要判断栈空

　　栗子3：　　

　　下列数据结构具有记忆功能的是？C

　　A.队列

　　B.循环队列

　　C.栈

　　 D.顺序表

　　　解释：

　　栈的特点是FILO，后进栈的先出栈，所以你对一个栈进行出栈操作，出来的元素肯定是你最后存入栈中的元素，所以栈有记忆功能。
　　而队列是先进先出，你取队列的第一个元素，得到的是你最先存入队列的元素，而不是上一个存入队列的元素，所以队列没有记忆功能。
　　可以用浏览网页的情况来理解，我们在浏览第一个网页A，点网页里的一个标题，进入网页B，再在网页B里点击一个标题，进入网页C，这时连续按后退退回网页A，这说明浏览网页有记忆功能，栈的原理跟这差不多，所以说它有记忆功能，自己再想象一下

　　栗子4：

package mianshiti;
import java.util.*;
public class Stacks {
	static String[] months={"January","February","March","April","May","June","July","August",
		"September","October","November","December"};

	public static void main(String[] args) {
		Stack stk=new Stack();
		for(int i=0;i<months.length;i++){
			stk.push(months[i]+"");
		}
		System.out.println("stk="+stk);
		stk.addElement("The last line");//在末尾添加元素
		System.out.println("element 5="+stk.elementAt(5));
		System.out.println("popping elements:");
		while(!stk.empty())
			System.out.println(stk.pop());
	}
}

　　栗子5：栈底层实现是数组

MyStack
package cn.itcast;

public class MyStack {
    //底层实现是一个数组
    private long[] arr;
    private int top;//设置栈顶
    /*
     * 默认构造函数*/
    public MyStack(){
        arr=new long[10];
        top=-1;  //空栈top=-1,用top变量来指示栈顶元素在数组中的位置。当栈中存在一个元素时，top=1
    }
    /*
     * 带参数的构造方法，参数为数组初始化大小*/
    public MyStack(int maxsize){
        arr=new long[maxsize];
        top=-1;
    }

    /*添加数据*/
    public void push(int value){
        arr[++top]=value;//首先要对top进行递增，因为初始的top为-1
    }

    /*移除数据*/
    public long pop(){
        return arr[top--];
    }

    /*查找数据*/
    public long peek(){
        return arr[top];
    }

    /*判断是否为空*/
    public boolean isEmpty(){
        return top==-1;
    }

    /*判断是否满了*/
    public boolean isFull(){
        return top==arr.length-1; //
    }
}

TestMyStack

package cn.itcast;

public class TestMyStack {

    public static void main(String[] args) {
        MyStack ms=new MyStack(4);//初始值为4，里面能存放4个数，调用带参数的构造函数的
        ms.push(23);
        ms.push(12);
        ms.push(1);
        ms.push(90);
        System.out.println(ms.isEmpty());
        System.out.println(ms.isFull());
        System.out.println(ms.peek());//查找栈顶元素

        while(!ms.isEmpty()){
            System.out.print(ms.pop()+",");
        }
        System.out.println(ms.isEmpty());
        System.out.println(ms.isFull());
    }

}

3.栈的应用

　　后缀，中缀，前缀，三种表达式

　　求中缀表达式转为后缀表达式的简单方法：

    * 将中缀表达式中所有的子表达式按计算规则用嵌套括号括起来

    ** 顺序将每对括号中的运算符移到相应的括号的后面

    *** 删除所有的括号

 

例如，将中缀表达式8-（3+5）*（5-6/2）转换成后缀表达式

执行第一步后为：（8-（（3+5）*（5-（6/2））））

执行第二步后为：（8（（35）+（5（62）/）-）*）-

执行第三步后为：8 3 5 +5 6 2 / - * -

　　中缀表达式转换为前缀表达式的简单方法：就是把运算符移到相应的括号前面

例如：a+b*c-(d+e)

执行第一步后为：((a+(b*c))-(d+e))

执行第二步后为：-(+(a*(bc))+ (de))

执行第三步后为：-+a*bc+de

　　后缀转中缀

　　规则：从左到右遍历表达式的每个数字和符号，遇到数字就进栈，遇到是符号，就将处于栈顶两个数字出栈，进行运算，运算结果进栈，一直到最终获得结果。

　　后缀式 ab+cd+/可用表达式（ ）来表示（ a+b）/（c+d）

　　过程如下：

　　a入栈

　　b入栈

　　遇到+号，取栈里的两个操作数，即a和b，计算a+b，结果入栈

　　c入栈

　　d入栈

　　遇到+号，取栈里的两个操作数，即c和d，计算c+d，结果入栈

　　遇到/，取栈里的两个操作数，即（a+b）和（c+d），计算（ a+b）/（c+d）

4.队列

　　只允许在一端进行插入操作，另一端进行删除操作的线性表

　　允许插入的一端是队尾，允许删除的一端是队头

　　所谓的入队列操作就是在队尾追加，不需要移动任何元素，时间复杂度是O(1)

　　而出队则是在队头操作，所有的元素都得向前移动，以保证队列的队头不为空，时间复杂度是O(n)

　　循环队列

　　front指针指向队头元素，rear指针指向队尾元素的下一个位置。

　　队列满的条件：

　　(rear+1)%QueueSize==front;//QueueSizeb表示队列的最大尺寸

　　取模%，就是防止最大下标位置越界。如：rear+1=59+1=60，而数组中最大下标是59而无60，这样取余（取模）就可以避免此类问题。

　　计算队列长度的公式：

　　(rear-front+QueueSize)%QueueSize

　　栗子1：

　　设有一个用数组Q[1..m]表示的环形队列，约定f为当前队头元素在数组中的位置，r为队尾元素的后一位置(按顺时针方向),若队列非空，则计算队列中元素个数的公式应为()

　　(m+r-f) mod m

　　栗子2:

　　若以1234作为双端队列的输入序列,则既不能由输入受限的双端队列得到,也不能由输出受限的双端队列得到的输出序列是(C)　　

　　　　A.1234

　　　　B.4132

　　　　C.4231

　　　　D.4213

　　解释：双端队列是一种同时具有队列和栈的性质的一种数据结构，在队列的两头都可以进行插入和删除的操作；

　　输入受限的双端队列是指只能从队列一端输入，可以从两端输出的双端队列；

　　同理，输出受限的双端队列是指只能从队列一端输出，可以从两端输入的双端队列；

　　如果双端队列允许从一端输入，从一端输出，则是普通的队列，如果双端队列只允许从一端输入和输出则是栈。

 　　
　　

 

/*添加数据，从队尾插入
     * */
    public void insert(long value){
        arr[++end]=value;
        elements++;
    }

    /*
     * 删除数据，从队头删除
     * */
    public long remove(){
        elements--;
        return arr[front++];
    }　　

　　　　发生了角标越界，是因为在end不断的增加，当再增加一个元素的时候，end又加1了，这样就越界了。

　　　所以要进行循环，就是end到队尾的时候，再变成end=-1

栗子：

MyCycleQueue
package cn.itcast;
/*列队类
 * */
public class MyCycleQueue {
    //底层使用数组
    private long[] arr;
    //有效数据的大小
    private int elements;
    //队头
    private int front;
    //队尾
    private int end; 

    /*默认构造方法
     * */
    public  MyCycleQueue(){
        arr=new long[10];
        elements=0;
        front=0;
        end=-1;
    }

    /*
     * 带参数的构造方法，参数为数组的大小*/
    public  MyCycleQueue(int maxsize){
        arr=new long[maxsize];
        elements=0;
        front=0;
        end=-1;
    }

    /*添加数据，从队尾插入
     * */
    public void insert(long value){
        if(end==arr.length-1){//判断是否队满
            end=-1;
        }
        arr[++end]=value;
        elements++;
    }

    /*
     * 删除数据，从队头删除
     * */
    public long remove(){
        long value=arr[front++];//首先取得这个数，再将队头后移了一位
        if(front==arr.length){//判断队列是否为空
            front=0;
        }
        elements--;
        return value;
    }

    /*
     * 查看数据，从队头查看
     * */
    public long peek(){
        return arr[front];
    }

    /*
     * 判断是否为空
     * */
    public boolean isEmpty(){
        return elements==0;
    }

    /*判断是否满了
     * */
    public boolean isFull(){
        return elements==arr.length;
    }
}