POJ1052 Plato's Blocks

题目来源：http://poj.org/problem?id=1052

题目大意：

　　把1*1*1的小立方体通过粘接相邻面组成大的立方体的形状。如下图所示：

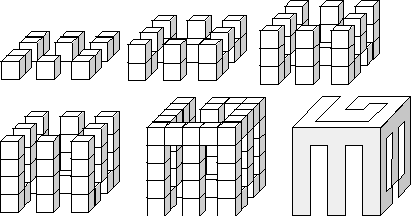
　　一层一层地堆叠，立方体从三个方向的投影会分别形成三个字母的形状："E" "G" "B"

　　科学家们想知道哪些投影形状的组合是可能出现的。写一个程序判断给定的投影图形组合是否可能出现。

输入：由一系列数据集组成。每个用例第一行为一个整数n(1<=n<=20)，表示大立方体的边长。接下来的3*n行为给出的投影图形。每n行表示一个面的投影，'X'表示产生了影子，'-'表示光线穿过。n为0时表示输入结束。

输出：如果给出的组合可能产生，输出：Valid set of patterns 否则输出 Impossible combination 格式见sample.

---

Sample Input

5
XXXXX
X----
X--XX
X---X
XXXXX
XXXXX
X----
XXXXX
X----
XXXXX
XXXXX
X---X
XXXX-
X---X
XXXXX
3
X--
-X-
--X
XX-
XXX
-XX
-XX
XXX
XX-
0

Sample Output

Data set 1: Valid set of patterns
Data set 2: Impossible combination

---

本题也属于模拟吧。首先需要把题目看懂。

首先，对于每个给出的投影图像，可能对应8种情况：通过旋转和镜像的变换得到。那么三个面总共有8*8*8种组合，枚举所有的组合，能找到符合条件的立方体能说明组合是可能出现的，否则不可能。

通过正向构造立方体比较麻烦，可以用“逆向”的方法。具体来说，首先根据给定的立方体大小，首先初始化一个完整的立方体。然后对于投影图形中被光线穿透的格子，“挖”去立方体对应的部分。

然而对每个面这样处理后得到的残留图形并不一定还能形成给定的三个投影，所以需要检验。除了检验投影还要检验它的连通性(dfs)。

代码中循环很多，要小心。

 //////////////////////////////////////////////////////////////////////////
 //        POJ1052 Plato's Blocks
 //        Memory: 396K        Time: 16MS
 //        Language: C++        Result: Accepted
 //////////////////////////////////////////////////////////////////////////

 #include <iostream>

 using namespace std;
 int n;
 int face[][][][];
 int cube[][][];
 int visited[][][];

 bool input() {
     cin >> n;
     if (n == ) return false;
     char c;
     for (int t = ; t < ; ++t) {
         for (int i = ; i < n; ++i) {
             for (int j = ; j < n; ++j) {
                 cin >> c;
                 if (c == 'X') face[t][][i][j] = ;
                 else face[t][][i][j] = ;
             }
         }
     }
     return true;
 }

 void r_m() {
     //rotation
     for (int t = ; t < ; ++t) {
         for (int k = ; k <= ; ++k) {
             for (int i = ; i < n; ++i) {
                 for (int j = ; j < n; ++j) {
                     face[t][k][i][j] = face[t][k - ][j][n - i - ];
                 }
             }
         }
     }
     //mirror
     for (int t = ; t < ; ++t) {
         for (int k = ; k < ; ++k) {
             for (int i = ; i < n; ++i) {
                 for (int j = ; j < n; ++j) {
                     face[t][k + ][i][j] = face[t][k][i][n - j - ];
                 }
             }
         }
     }
 }

 void MakeCube(int a, int b, int c) {
     for (int i = ; i < n; ++i) {
         for (int j = ; j < n; ++j) {
             if (face[][a][i][j] == ) {
                 for (int k = ; k < n; ++k) {
                     cube[i][j][k] = ;
                 }
             }
         }
     }
     for (int i = ; i < n; ++i) {
         for (int j = ; j < n; ++j) {
             if (face[][b][i][j] == ) {
                 for (int k = ; k < n; ++k) {
                     cube[k][i][j] = ;
                 }
             }
         }
     }
     for (int i = ; i < n; ++i) {
         for (int j = ; j < n; ++j) {
             if (face[][c][i][j] == ) {
                 for (int k = ; k < n; ++k) {
                     cube[i][k][j] = ;
                 }
             }
         }
     }
 }

 bool check(int a, int b, int c) {
     for (int i = ; i < n; ++i) {
         for (int j = ; j < n; ++j) {
             if (face[][a][i][j] == ) {
                 bool flag = ;
                 for (int k = ; k < n; ++k) {
                     if (cube[i][j][k]) {
                         flag = ;
                         break;
                     }
                 }
                 if (flag == ) {
                     return false;
                 }
             }
         }
     }
     for (int i = ; i < n; ++i) {
         for (int j = ; j < n; ++j) {
             if (face[][b][i][j] == ) {
                 bool flag = ;
                 for (int k = ; k < n; ++k) {
                     if (cube[k][i][j]) {
                         flag = ;
                         break;
                     }
                 }
                 if (flag == ) {
                     return false;
                 }
             }
         }
     }
     for (int i = ; i < n; ++i) {
         for (int j = ; j < n; ++j) {
             if (face[][c][i][j]) {
                 bool flag = ;
                 for (int k = ; k < n; ++k) {
                     if (cube[i][k][j]) {
                         flag = ;
                         break;
                     }
                 }
                 if (flag == ) {
                     return false;
                 }
             }
         }
     }
     return true;
 }

 void dfs(int i, int j, int k) {
     if (i <  || i >= n || j <  || j >= n || k <  || k >= n) {
         return ;
     }
     if (cube[i][j][k] ==  || visited[i][j][k] == ) {
         return;
     }
     visited[i][j][k] = ;
     dfs(i - , j, k);
     dfs(i + , j, k);
     dfs(i, j - , k);
     dfs(i, j + , k);
     dfs(i, j, k - );
     dfs(i, j, k + );
 }

 bool connectivity() {
     memset(visited, , sizeof(visited));
     for (int i = ; i < n; ++i) {
         for (int j = ; j < n; ++j) {
             if (cube[i][j][]) {
                 dfs(i, j, );
                 for (int a = ; a < n; ++a) {
                     for (int b = ; b < n; ++b) {
                         for (int c = ; c < n; ++c) {
                             if (cube[a][b][c] && visited[a][b][c] == ) {
                                 return false;
                             }
                         }
                     }
                 }
                 return true;
             }
         }
     }
 }

 bool IsValid() {
     r_m();
     for (int i = ; i < ; ++i) {
         for (int j = ; j < ; ++j) {
             for (int k = ; k < ; ++k) {
                 memset(cube, , sizeof(cube));
                 MakeCube(i, j, k);
                 if (check(i, j, k) && connectivity()) {
                     return true;
                 }
             }
         }
     }
     return false;
 }

 int main(void) {
     int case_id = ;
     while (input()) {
         cout << "Data set " << ++case_id << ": ";
         if (IsValid()) {
             cout << "Valid set of patterns" << endl;
         } else {
             cout << "Impossible combination" << endl;
         }
     }
     system("pause");
     return ;
 }