JDK学习---深入理解Comparator、TreeSet、TreeMap为什么可以排序

　　我本来打算仔细的去分析分析TreeSet和TreeMap排序规则，并且从底层实现和数据结构入手。当我去读完底层源码以后，我感觉我就的目标定的太大了，单单就是数据结构就够我自己写很久了，因此我决定先易后难，先把底层源码以及最直接的数据结构分析一下，至于底层的平衡二叉树以及红黑二叉树，我就不过多去介绍，因为这是底层源码优化用的，与直接实现代码没有多大关系，感兴趣的也可以去仔细研究。

　　树: 树是n ( n >=0)个节点的有限集。n = 0时称为空树。在任意一颗非空树种中: (1)有且仅有一个特定的称为根（Root）的节点；（2）当n > 1时，其余节点可分为m（m > 0）个互不相交的有限集T1、T2、T3......Tm,其中集合本身又是一颗树，并且称为根的子树。如下图：

　　　节点的子树的根称为该节点的孩子，相应地，该节点称为孩子的双亲。为什么叫双亲，而不是父母呢？因为对于节点来说其父母同体，唯一的一个，所以只能把它称为双亲。同一个双亲的孩子之间称为兄弟。如下图：

树的其他相关概念：

　　层：节点的层次是从根开始定义的，根称为第一层，根的孩子称为第二层。树中节点的最大层次称为树的高度或深度。如下图：

　　　　

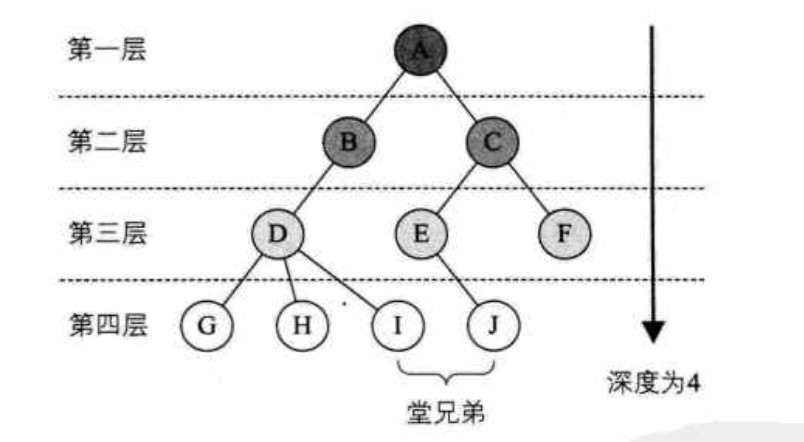
　　如果将树中节点的各个子树看成从左到右是有次序的，不能互换的，则称该树为有序树，否则称为无序树。

　　

 二叉树

　　二叉树：二叉树是n （n >= 0）个节点的有序集合，该集合或者为空集（称为空二叉树），或者由一个根节点和两颗互不相交的、分别称为根节点的左子树和右子树的二叉树组成。

 　　二叉树的特点:

　　　　1、每个节点最多有两颗子树，所以二叉树中不存在度大于2的节点。注意不是只有两颗子树，而是最多有。没有子树或者有一颗子树都是可以的。

　　　　2、左子树和右子树是有顺序的，次序不能任意颠倒。

　　　　3、即使树种某节点只有一颗子树，也要区分它是左子树还是右子树。因为左子树和右子树是完全不同的概念，区别特别重要。

二叉树的形态：

　　　 1、空二叉树

　　　  2、只有一个根节点

　　　  3、根节点只有左子树

　　　  4、根节点只有右子树

　　　 5、根节点既有左子树，又有右子树。对应下面5附图：

　　

　　

　　 二叉树的存储结构：

　　　　　1、二叉树的顺序存储结构

　　　　　2、二叉树的连式存储结构（二叉链表）

　　　　

　　　　　顺序存储结构：顺序存储结构就是用一维数组存储二叉树中的节点，并且节点的存储，也就是数组的下标要能体现节点之间的逻辑关系，比如双亲与孩子的关系，左右兄弟的关系等。　　

　　　　　　存储前：

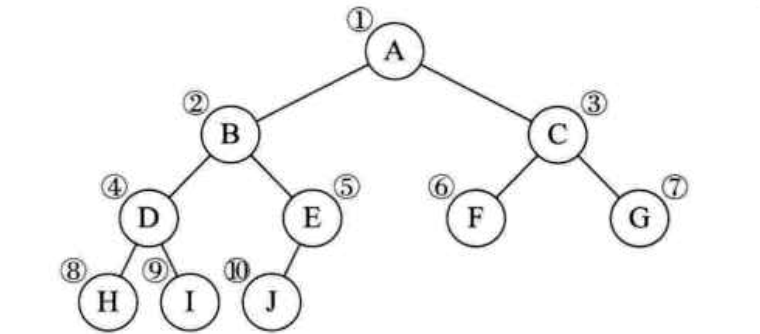
　　　　存储后：

　　　　　　

　　　　二叉链表：二叉树每个节点最多有2个孩子，所以为它设计一个数据域和两个指针域。结构图如下：

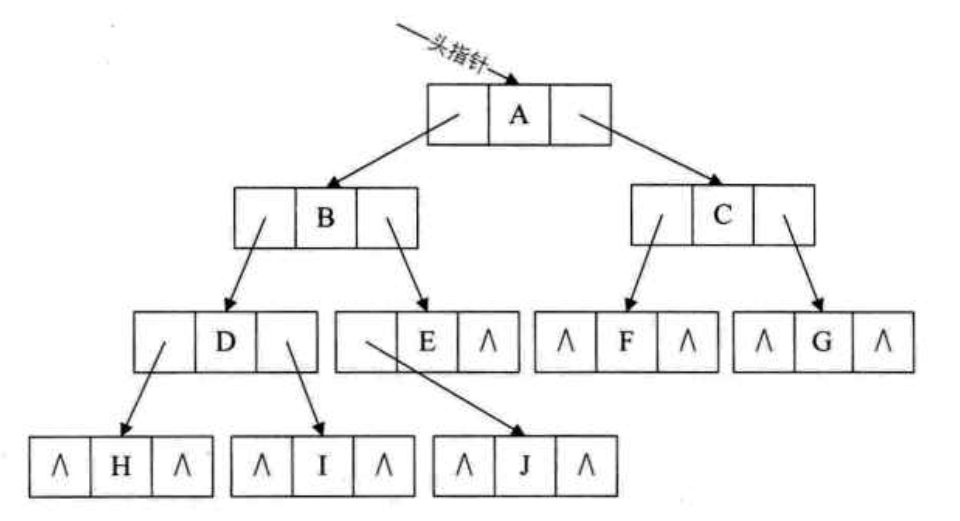
　　二叉树的遍历：前序遍历、中序遍历、后序遍历、层序遍历。具体遍历我就不累赘了。

　　　　　　

二叉排序树：　　

　　　　二叉排序树：二叉排序树，又称为二叉查找树。它或者是一颗空树，或者是具有下列性质的二叉树。

　　　　    1、若它的左子树不空，则左子树上所有节点的值均小于它的根结构的值。

　　　　　2、若它的右子树不空，则右子树上所有节点的值均大于它的根节点的值。

 　　　　  3、它的左、右子树也分别为二叉排序树。

　　　　

　　　　典型案例就是数字游戏：我在纸上写好了一个100以内的正整数数字，大家来猜我写的是哪一个数字。注意，你们在才对过程中我只会回答“大了” 或 “ 小了 ”。

　　　　其实，这是一个很典型的折半查找法，就是对二叉排序树的典型应用。如下图：

　　　　

源码解读：

首先，我们看看TreeMap中需要用到的二叉树的类结构：

static final class Entry<K,V> implements Map.Entry<K,V> {
        K key;
        V value;
　　　　 
　　　　 //记录左子树
        Entry<K,V> left = null;
　　　　　//记录右子树
        Entry<K,V> right = null;
　　　　 //记录双亲节点
        Entry<K,V> parent;
　　　　 //红黑二叉树使用的根节点默认颜色
        boolean color = BLACK;

        /**
         * Make a new cell with given key, value, and parent, and with
         * {@code null} child links, and BLACK color.
         */
        Entry(K key, V value, Entry<K,V> parent) {
            this.key = key;
            this.value = value;
            this.parent = parent;
        }
//省略很多具体的方法

TreeMap成员变量和构造方法：

 　　//排序规则辅助类
    private final Comparator<? super K> comparator;
　　//记录根节点
    private transient Entry<K,V> root = null;

    /**
     * The number of entries in the tree
     */
    private transient int size = 0;

    /**
     * The number of structural modifications to the tree.
     */
    private transient int modCount = 0;

    public TreeMap() {
        comparator = null;
    }
　　//本文重点分析的构造方法
    public TreeMap(Comparator<? super K> comparator) {
        this.comparator = comparator;
    }

    public TreeMap(Map<? extends K, ? extends V> m) {
        comparator = null;
        putAll(m);
    }

    public TreeMap(SortedMap<K, ? extends V> m) {
        comparator = m.comparator();
        try {
            buildFromSorted(m.size(), m.entrySet().iterator(), null, null);
        } catch (java.io.IOException cannotHappen) {
        } catch (ClassNotFoundException cannotHappen) {
        }
    }

构造方法比较多，我本篇稳重重点说排序功能，因此我就选  public TreeMap(Comparator<? super K> comparator) 方法进行突破。而Comparator就是JDK自带的排序辅助类，这个我们后面讲。

分析put方法：public V put(K key, V value) {        Entry<K,V> t = root;

　　　　
　　　　//如果根节点为null将传入的键值对构造成根节点
        if (t == null) {
            compare(key, key); // type (and possibly null) check
　　　　　　　//根节点没有父节点，所以传入null
            root = new Entry<>(key, value, null);
            size = 1;
            modCount++;
            return null;
        }
　　　　　//记录比较结果
        int cmp;
        Entry<K,V> parent;
        // split comparator and comparable paths
        Comparator<? super K> cpr = comparator;

　　　　//以下的if...else非常重要，主要是定位具体的节点（这个节点是作为父节点的，我们将新传入的key/value插入到这个具体的节点下）
　　　　//有比较器的情况
        if (cpr != null) {
　　　　　　　//dowhile实现在root为根节点移动寻找传入键值对需要插入的位置
            do {
　　　　　　　　　　//记录将要被插入新的键值对的节点
                parent = t;
　　　　　　　　　　//比较器，按照自定义的规则返回结果
                cmp = cpr.compare(key, t.key);
　　　　　　　　　　//插入的key较大
                if (cmp < 0)
                    t = t.left;
　　　　　　　　   //插入的key较小
                else if (cmp > 0)
                    t = t.right;
　　　　　　　　　　//如果key相等，则直接替换value
                else
                    return t.setValue(value);
            } while (t != null);
        }
　　　　　//没有传入比较器
        else {
            if (key == null)
                throw new NullPointerException();
            Comparable<? super K> k = (Comparable<? super K>) key;
　　　　　　　　//与上方的do..while一样，知识比较的规则不同
            do {
                parent = t;
                cmp = k.compareTo(t.key);
                if (cmp < 0)
                    t = t.left;
                else if (cmp > 0)
                    t = t.right;
                else
                    return t.setValue(value);
            } while (t != null);
        }
　　　　　//没有找到相同的key，才会有此以下的方法操作。否则直接在上方就直接t.setValue(value)了
　　　　　//根据key、value以及双亲节点，创建一个新的节点
        Entry<K,V> e = new Entry<>(key, value, parent);
　　　　　//如果最后一次判断的结果，确认新节点是父节点的左孩子，还是右孩子；为什么说是最后一次判断的结果呢？因为上面的if...else...中都有while方法，而这个while就是为了找这个最后的一次比较的结果
        if (cmp < 0)
            parent.left = e;
        else
            parent.right = e;

　　　　　//此方法我就不介绍了，涉及到红黑二叉树以及二叉树的摇摆，对二叉树进行优化操作
        fixAfterInsertion(e);
        size++;
        modCount++;
        return null;
    }

至此，我们发现，二叉树的插入式根据cmp的值进行操作的，小于0就放在左子树，大于0就放在右子树。这不就是典型的二叉排序树啊？还记得之前说的猜数字游戏么？

由此可知：

　　1、TreeMap底层的二叉树是按照二叉排序树的结构进行存储的，左侧小于根节点，右侧大于根节点

　　2、至于是大于父节点，还是小于父节点，那就是我们自己定义的Comparator比较器的事情了。正常的情况下，我们知道1小于2；但是如果是自定义比较器，那么我们完全可以自定义1大于2；这种情况下也就出现了所谓的升序和降序了。

说了这么多，也许好多人还不是很明白。那么接下来，我就举几个例子进行说明吧：

案例1：根据key的长度升序

    public <T> void test1()
    {
        Map<String, String> map = new TreeMap<String, String>(
                new Comparator<String>()
                {
                    public int compare(String o1, String o2)
                    {
                        return o1.length() - o2.length();
                    }
                });

        map.put("hello", "我是hello");
        map.put("jk", "我们认识吗？");
        map.put("oooooo", "我要去香山看红叶");

        Set<Entry<String, String>> set = map.entrySet();
        System.out.println("-----------------test1 : ");
        for (Iterator iter = set.iterator(); iter.hasNext();)
        {
            Entry<String, String> entry = (Entry<String, String>) iter.next();
            System.out.println(entry.getKey() + " : " + entry.getValue());
        }
    }

这个案例是升序，因为TreeMap调用compare(T o1, T o2)传入的是可以的值，因此，此处o1是新插入的key，而o2则是我们源码提到的do...while...中说道的找到的最后一次排序的key。而如果我们想降序，只要将compare(T o1, T o2)实现方法中的 return o1.length() - o2.length();改成 return o2.length() - o1.length();即可。允许结果如下图：

-----------------test1 :
jk : 我们认识吗？
hello : 我是hello
oooooo : 我要去香山看红叶

那么假如我们按照value进行排序，那又该怎么办呢？我们看过底层的源码实现，TreeMap没有提供说put的时候，可以进行对value的操作，因此要想直接通过TreeMap对value的值进行排序，那是不现实的。那如果我们的业务非要对value进行排序又该怎么办呢？如下：

//根据value排序
    public void sortByValue()
    {
        Map<String, String> map = new HashMap<String, String>();
        map.put("a3", "dddd");
        map.put("d", "aaaa");
        map.put("b435", "cccc");
        map.put("c6323", "bbbb");

        List<Entry<String, String>> list = new ArrayList<Entry<String, String>>(
                map.entrySet());

        Collections.sort(list, new Comparator<Map.Entry<String, String>>()
        {
            // 升序排序
            public int compare(Entry<String, String> o1,Entry<String, String> o2)
            {
                return o1.getValue().compareTo(o2.getValue());
            }
        });

        System.out.println("sortByValue =" + list);
    }

看了这个实现，其实我们并没有对HashMap进行排序，而是在遍历的时候对存放二叉树Entry的list进行排序的，运行结果如下：

sortByValue =[d=aaaa, c6323=bbbb, b435=cccc, a3=dddd]

TreeSet源码：

TreeSet的构造方法：　　

 TreeSet(NavigableMap<E,Object> m) {
        this.m = m;
    }

    public TreeSet() {
        this(new TreeMap<E,Object>());
    }

    public TreeSet(Comparator<? super E> comparator) {
        this(new TreeMap<>(comparator));
    }

    public TreeSet(Collection<? extends E> c) {
        this();
        addAll(c);
    }

    public TreeSet(SortedSet<E> s) {
        this(s.comparator());
        addAll(s);
    }

接下来，我将会围绕 public TreeSet(Comparator<? super E> comparator) 进行拓展：

 public TreeSet(Comparator<? super E> comparator) {
        this(new TreeMap<>(comparator));
    }

而TreeMap上面已经分析过了，我们知道TreeMap默认的是对key进行排序的，而TreeMap的构造方法居然在构建一个TreeMap方法，接下来接续分析

add方法：

 public boolean add(E e) {
        return m.put(e, PRESENT)==null;
    }

remove方法：

 public boolean remove(Object o) {
        return m.remove(o)==PRESENT;
    }

first方法、last方法：

 public E first() {
        return m.firstKey();
    }

    /**
     * @throws NoSuchElementException {@inheritDoc}
     */
    public E last() {
        return m.lastKey();
    }

iterator方法：

  public Iterator<E> iterator() {
        return m.navigableKeySet().iterator();
    }

看完实现方法，全部是对m进行操作，而这个m是什么呢？就是我们之前的TreeMap。TreeMap已经分析过了，而TreeSet只是在调用TreeMap而已，因此废话就不多说了。

总结：

　1、TreeMap只能通过对key进行排序操作，无法直接对value进行排序操作；而TreeSet的底层实现则是TreeMap，因此TreeSet也value也就是TreeMap的key，因此TreeSet是可以对value进行各种排序的；

　2、Comparator根本不能排序，它只是自定义的一种规则；而这个规则，TreeMap已经在底层对它进行封装和调用了；

　3、如果我们想要对TreeMap的value进行操作的话，可以借助集合辅助类Collections进行操作