【学时总结】◆学时·VII◆ 高维DP

◆学时·VII◆ 高维DP

自学之余，偶遇DP……

---

◇ 算法概述

顾名思义——一种处理多方面状态的DP，这种DP特点是……每一维的大小都不算太大（不然用dp数组存储下来内存会炸），而且枚举时容易超时……（一般来说，DP的复杂度为每一维的可取值之积。毕竟是乘积，很容易炸掉）。

众所周知，除了状压DP，一般的DP都是每一维表示了一个方面的状态，因此我们需要按照一定顺序枚举状态。

高维DP的大多数题中，各个方面的状态是互相关联、影响的，因此注意状态之间的互相限制是高维DP的难点，这也导致高维DP非常费脑子——状态转移方式奇多无比。

还有什么注意事项就看下面的例题吧~

---

◇ 例题选讲

（好像只找到一道题，之后找到其他的好题再补上吧……QwQ）

【Codeforces 14E】Camels +传送门+

· 题目大意

n个数依次为A_1~n，当且仅当第i个数(1<i<n)满足 A_i-1<A_i 且 A_i>A_i+1 ，我们称A_i是一个驼峰；当且仅当 A_i-1>A_i 且 A_i<A_i+1 ，我们称 A_i 是一个谷底。已知 1≤A_i≤4 ，求恰好形成t个驼峰的方案数。

· 解析

这道题是DP没任何问题，统计类一般是DP（其他就是暴力DFS[补充 2018-08-09 08:04:21]以及组合数学推导公式）……

现在就可以开始找有哪些方面的状态了：

数的位置 i；第 i 个位置上的数 j ；第 i 个数在第 k 个驼峰上（从上升段开始到下降段结束）；第 i 个数在驼峰的上升/下降段。

注意：我们并不需要找到所有的状态，那些关联很紧密（几乎一一对应的）就不需要用了，我们只需要找相对有独立性但仍能影响其他状态的状态。

有了这些状态，我们就可以进行状态转移了。

提示：如果你发现你找出的状态无法互相转移，不要犹豫，换一种方法吧……

分几种情况讨论（Tab. 这里将驼峰算作上升段，谷底算作下降段）：

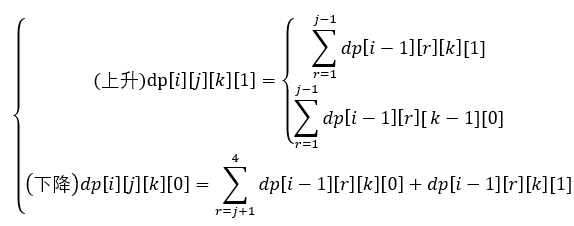
上升的第一种dp[i-1][r][k][1]就是i和i-1在同一个驼峰上且都处于上升段，直接相加；

上升的第二种dp[i-1][r][k-1][0]就是i-1是前一个驼峰上的下降段的末尾（谷底），直接相加；

下降的第一种dp[i-1][r][k][0]就是i-1和i在同一个驼峰上，都处于下降段，直接相加；

下降的第二种dp[i-1][r][k][1]就是i-1和i在同一个驼峰上，i-1处于上升段的末尾（驼峰），直接相加；

[补充 2018-08-09 16:09:51 - 由于一些reader不知道下面代码13~15行的初始化什么意思，这里加上]

由于题目规定最初的一段必须是上升的，为了避免下降的情况，我们从第2个数开始初始化，因为只有一个数时并看不出是上升还是下降，初始化第一个数显得没什么必要。dp[2][2][1][1]包含了 {1,2} ；dp[2][3][1][1] 包含了 {1,3},{2,3}；dp[2][4][1][1] 包含了 {1,4},{2,4},{3,4} 。这样就保证了1~2的段上一定是上升的！

· 源代码

 /*Lucky_Glass*/
 #include<cstdio>
 #include<cstring>
 #include<algorithm>
 using namespace std;
 const int MAXN=,MAXDIG=,MAXT=;
 typedef long long ll;
 ll dp[MAXN+][MAXDIG+][MAXT+][];
 //dp[i][j][k][r] 第i个数为j时在第k个驼峰上处于 r=1上升,r=0下降 状态
 int main()
 {
     int n,t;scanf("%d%d",&n,&t);
     dp[][][][]=;
     dp[][][][]=;
     dp[][][][]=;
     for(int i=;i<=n;i++)
         for(int j=;j<=;j++)
             for(int k=;k<=t;k++)
                 for(int r=;r<=;r++) //上一个数字
                 {
                     if(r<j)
                         dp[i][j][k][]+=dp[i-][r][k][];
                     if(r<j && k>)
                         dp[i][j][k][]+=dp[i-][r][k-][];
                     if(r>j)
                         dp[i][j][k][]+=dp[i-][r][k][],
                         dp[i][j][k][]+=dp[i-][r][k][];
                 }
     ll ans=;
     for(int i=;i<=;i++)
         ans+=dp[n][i][t][];
     printf("%lld\n",ans);
     return ;
 }

[补充 2018-08-09 20:44:09：作者终于找到一道好题了QwQ]

【UVA 10118】Free Candies +传送门+（Uva比较慢，这边是vjudge的链接）+传送门+

· 题目大意

有4堆糖果，每堆n个，糖果有不同的颜色。Little Bob有一个小篮子，可以装下5颗糖果。他每次可以拿出一堆糖果的顶部的糖果（一堆糖果拿完了就不能拿了）放进篮子里。每次取了糖果后，他会检查自己的篮子——如果里面有一对相同颜色的糖果，他就会取出那一对糖果放在自己的包里。

n不超过40，糖果的颜色用整数表示，该整数不超过20。

输入多组数据，每组数据第一行为n，以下n行每行4个整数，构成一个n行4列的矩阵，第i列自上至下描述了一堆糖果。输入以0结束。

计算最后Bob口袋里糖果最多有多少个，输出所得值除以2。

· 解析

由于n并不大，我们甚至能够储存一个n⁴的数组，于是我们就可以定义出DP状态——dp[pos[0]][pos[1]][pos[2]][pos[3]]，其中pos[i]表示现在第i堆糖果的顶部是原来第i堆糖果的第几个。

这样就非常好转移——每一次只会取出4堆糖果中的一堆糖果的顶部。但是比较麻烦的是判断篮子里是否有同样颜色的糖果，用递推处理的话没法判断取出糖果的先后性（这道题中顺序会影响答案 ？留给reader们想一想）。比较好处理先后顺序的是DFS，于是我们想到可以用记忆化搜索！由于对于每一种剩余糖果的情况都唯一对应一种得到糖果数量，所以满足DP所需要的性质。

在记忆化搜索中，需要下传一个vis（用二进制压缩），表示当前篮子里有哪几种颜色的糖果，又因为同种颜色的糖果达到两个，Bob就会把他们拿出去，所以同种颜色的糖果不会超过1个，也就可以二进制压缩了。当vis中存在5个元素，则篮子满了，而里面没有相同颜色的糖果，返回0（不赋值给dp）。

每次枚举4堆糖果中的一堆，如果那堆糖果没有取完，就尝试取出堆顶，更新vis。

其他还有什么就看代码了……

· 源代码

 /*Lucky_Glass*/
 #include<cstdio>
 #include<cstring>
 #include<algorithm>
 using namespace std;
 const int MAXN=;
 int n;
 int cdy[MAXN+][],dp[MAXN+][MAXN+][MAXN+][MAXN+]; //糖果，以及DP数组
 int pos[]; //pos[i]表示现在第i堆糖果的顶部是原来的第pos[i]个糖果
 int DP(int vis)
 {
     int fvis=vis,cnt=;
     while(fvis) cnt+=fvis%,fvis/=; //统计vis的元素数量，也就是篮子里的糖果数量
     if(cnt>=) return ;
     int A=pos[],B=pos[],C=pos[],D=pos[];
     if(dp[A][B][C][D]) return dp[A][B][C][D];
     for(int i=;i<;i++)
         if(pos[i]<=n) //未取空
         {
             int x=<<cdy[pos[i]][i]; //第pos[i]个元素的颜色
             pos[i]++; //取出
             if(vis&x) //vis中存在此种颜色
                 dp[A][B][C][D]=max(dp[A][B][C][D],DP(vis^x)+);
             else
                 dp[A][B][C][D]=max(dp[A][B][C][D],DP(vis|x));
             pos[i]--; //回溯
         }
     return dp[A][B][C][D];
 }
 int main()
 {
     //freopen("in.txt","r",stdin);
     while(~scanf("%d",&n) && n)
     {
         memset(dp,,sizeof dp);
         for(int i=;i<=n;i++)
             for(int j=;j<;j++)
                 scanf("%d",&cdy[i][j]);
         pos[]=pos[]=pos[]=pos[]=; //从堆顶开始取
         printf("%d\n",DP()); //一开始篮子里什么都没有
     }
     return ;
 }

---

The End

Thanks for reading!

- Lucky_Glass

（Tab：如果我有没讲清楚的地方可以直接在邮箱lucky_glass@foxmail.com email我，在周末我会尽量解答并完善博客~）