Geometric Search

几何搜索

平衡搜索树（BST）在几何方面的应用，处理的内容变成几何对象，像点，矩形。

1d range search

先来看一维的情况，一维的范围搜索是后面的基础，处理的对象是在一条线上的点。这是符号表的一个小拓展，多了范围查找（range search） 和范围计数（range count）即希望知道给定范围上有哪些点或是有多少点。

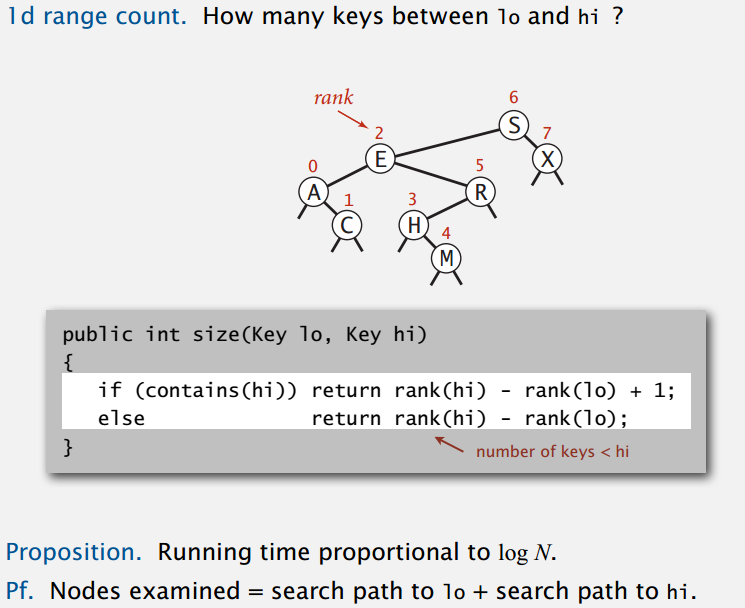
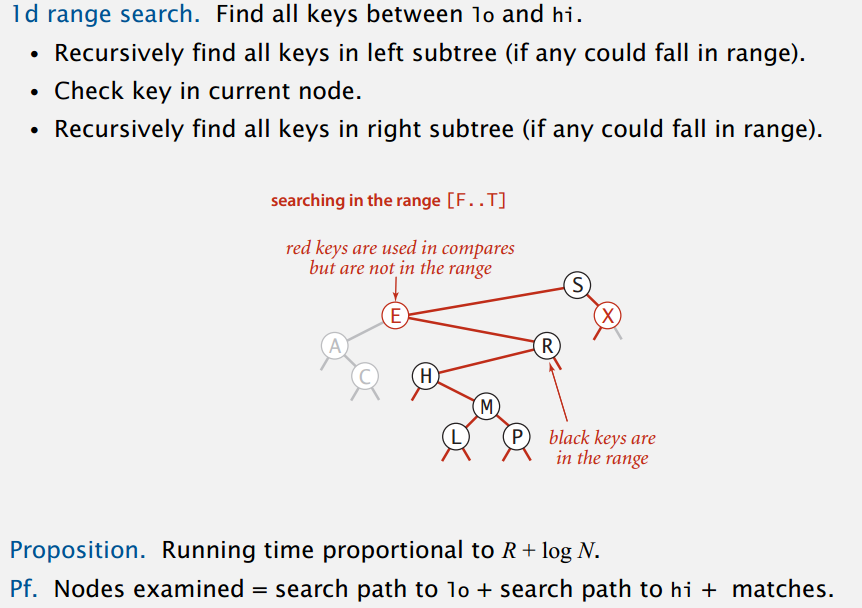
用无序链表来实现的话，插入直接放开头，但是范围查找和范围计数都需要正比于 N 的时间。用有序数组来实现的话，范围计数的时间复杂度是 logN 级别，范围查找是 R+logN 级别（范围内有 R 个点），插入为了维护有序性需要的时间也和 N 成正比。所以说，高效的实现得用 BSTs，插入和范围计数的时间复杂度都是 logN，范围查找的则是 R+logN。

范围计数：

范围查找：

line segment intersection

接着我们到二维，设想有很多水平或垂直的线段，现在希望找到所有交点。

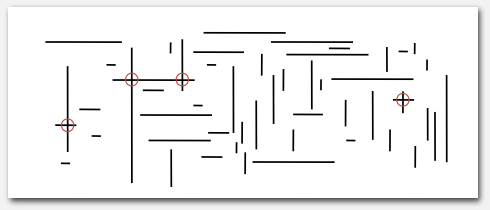
遍历检查所有可能组合会是平方级别的复杂度，显然是不可接受的，其实我们可以把问题转成上面一维的情况。

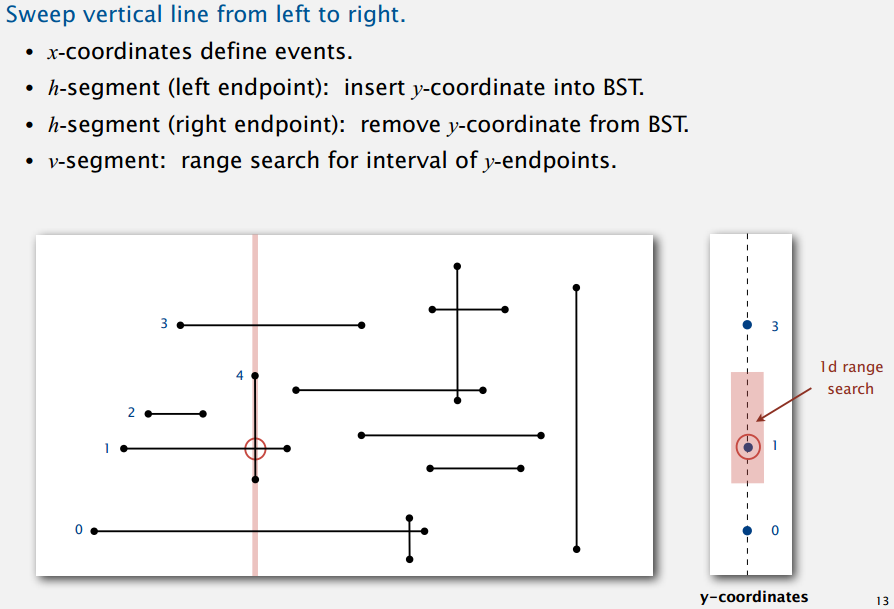
方便起见，这边的线段没有重合啥七七八八的情况。假想有一条垂直的线，从左扫到右，碰到水平线段的左端点就把该线段的 y 值放入 BST，碰到水平线段的右端点就把该线段的 y 值从 BST 中移除，碰到垂直线段就以该线段的上下端点为区间在 BST 中做范围计数。像上面的例图，点 2 已经从 BST 中移除了，点 4 是第一个垂直线段，范围查找发现有个点 1，也就发现了第一个交点。

kd trees

kd 树是 BSTs 的拓展（k 个维度），可以高效地处理空间中的点，十分灵活，在很多应用中很有用。就算不是几何问题，在数据库中你可能想知道收入在 1m - 10m 且年龄在 40 - 50 岁的人有哪些，这种场景也好用。

现在的例子正式从一维拓展到二维，范围查找和范围计数从区间上升到矩形，即希望知道平面上有哪些点或是有多少点在查询的矩形上。

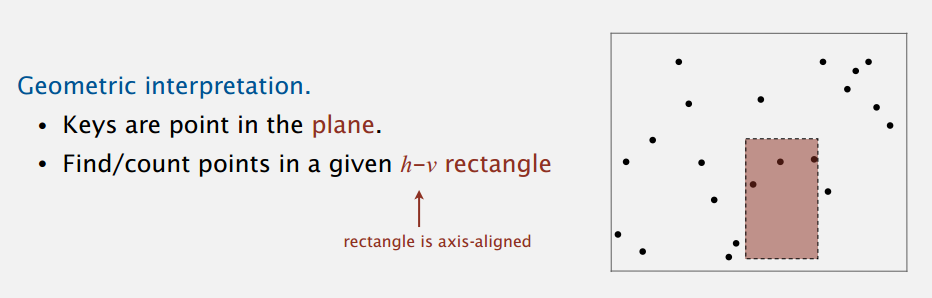
一个可能的做法是把平面用网格划分，比较理想状况下是这样的：

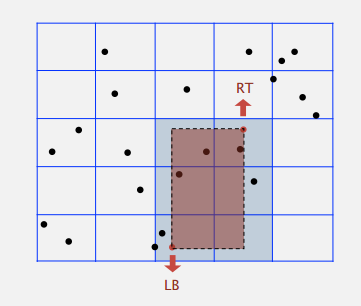
点的分布比较均匀，每个网格可以对应一个链表来表示在其中的点。范围查找的时候就检查涉及到的网格，不用遍历整个平面，从而提高搜索效率。

M * M 的网格，M 太大会浪费空间，太小每个网格会有好多点，N 个点可以考虑设为 \(\sqrt []{N}\)。但是吧，对于几何数据，聚集（clustering）是一个很常见的现象，没法均匀地分布在网格上，比如像下面的地图数据：

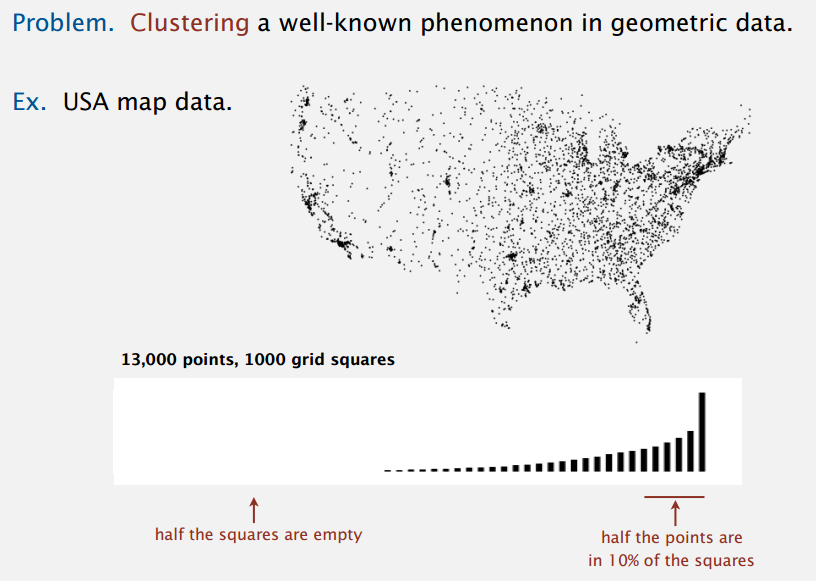
所以说，网格划分不大适合我们的应用场景，经常会有好多点在一格，不然开好多小格又会浪费空间。但是，空间划分的想法是好的，我们可以用树结构类似的递归把空间分成两半两半。

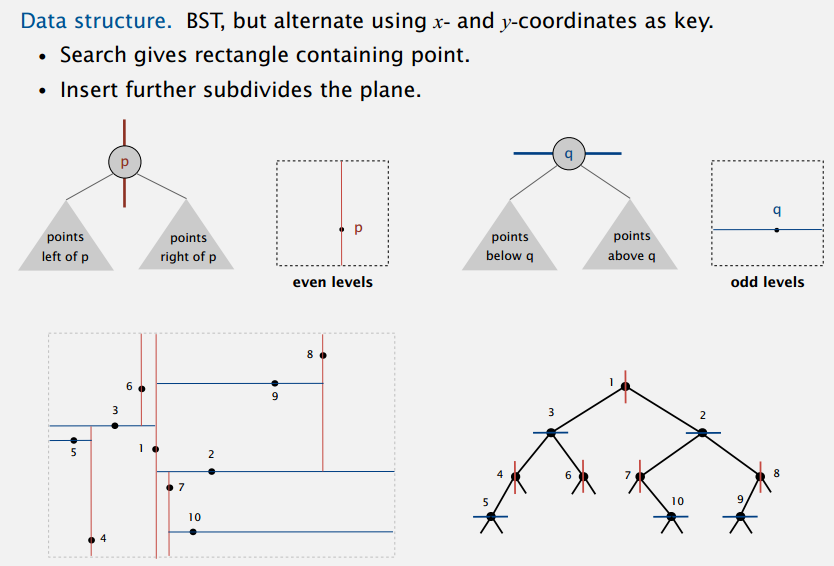
树节点的键交替用 x，y 坐标，左右孩子还是原来那样一个小一个大，在平面上来看就是点的上下或左右。

应用方面，举了范围查找和搜索最近邻居两个例子。

range search in a 2d tree

在 x 节点比较横坐标选左右，在 y 节点比较纵坐标选择上下，就是二分吧，一次砍掉一半搜索空间。

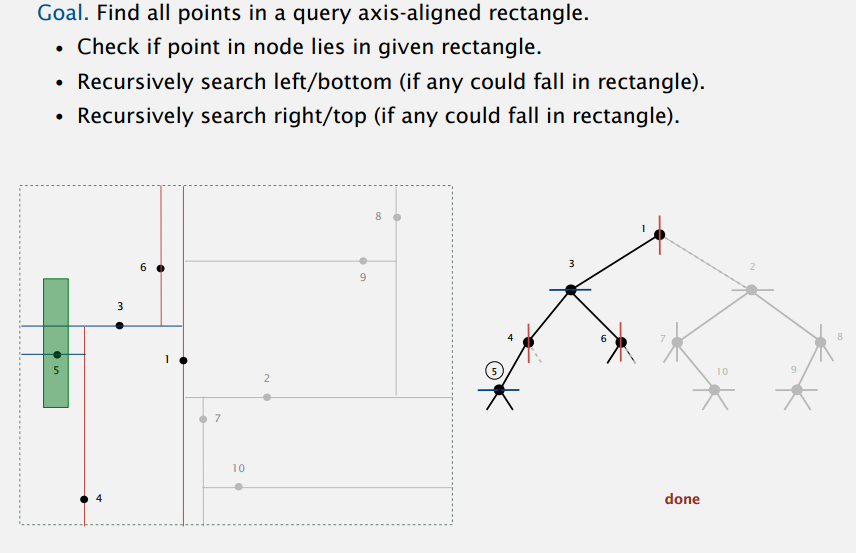
第一次点 1 不在查询矩形里，接着发现矩形在左边，右子树马上整个不要；接着点 1 的左孩子点 3 也不在矩形里，但 y 坐标在区间里所以上下都要搜索；点 4 和点 1 一样，只要搜索左边；现在找到点 5 在矩形里，两个孩子为空结束搜索；继续返回搜索点 3 的另一边，点 6 也只要搜索左边，为空结束，至此完成整个搜索过程。

典型情况下，2d 树的时间复杂度为 R+logN （R 是在矩形中的点的个数），但是吧，最坏情况下，即使树是平衡的，复杂度也是 \(R+\sqrt []{N}\) （课程说相关证明超纲不提）。可是，对于很多实际应用来说，2d 树易于实现而且也值得一用。

nearest neighbor search in a 2d tree

搜索过程类似，每次选择查询点所在的一边，虽然最近的点也可能在另外一边，但是一般来说在同一边的概率大，所以这里采取这样的选择。

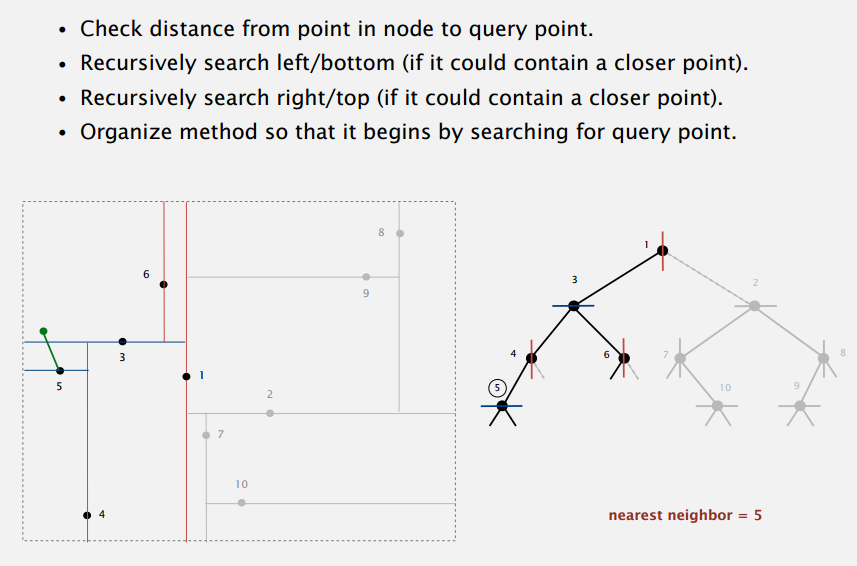
一路找下来，更新离查询点最近的距离和点。找到点 5 之后返回搜索点 4 的右边，为空继续返回搜索点 6 的右边，同样为空到了点 1 的右边。这里应该也可以有是否剪枝的判断，好像这次的编程作业就有这个，比如说现在点 5 到查询点的距离明显小于查询点到点 1 所在垂直红线的距离，那么点 1 的右子树就完全可以砍掉。

性能方面，典型情况是 logN，最坏情况是 N，我想了下，比如说点在圆上，然后查询点在圆心这样子。反正，一般来说，还是很高效的。

interval search trees

原来一维上的研究对象是点，现在再来看看一维下的区间（线段），问题是查找和给定区间有交集的区间。

还是用 BST 来表示，区间左端点为键（这里假定没有重复的左端点），同时在节点里保存后代最大的右端点。

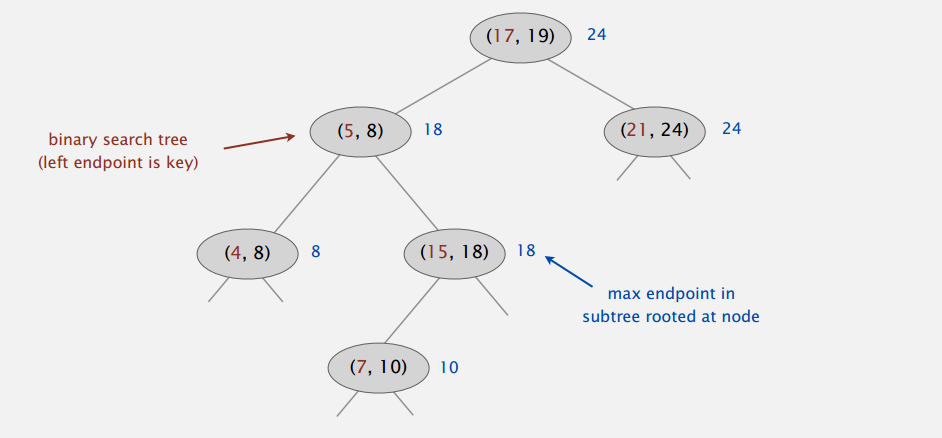
插入新的节点的时候，通过比较左端点来找到合适位置，然后看看路径上最大右端点是否要更新。

查找的时候，节点有交集就直接返回（先说找到任一相交区间），不然就把查询区间左端点和左孩子的最大右端点比较，前者比较大就可以砍掉左子树；后者比较大就需要查找左子树。要注意的是，第二种情况下，左子树可能还是没有相交的区间，然后！这个时候的右子树也是不用搜索的。

要是查询区间在左子树没有相交区间，右端点最大的那个区间的左端点 c 肯定在前面，而右子树的左端点又比左子树的大，所以就像上图那样可以不用找右边了。

实现上，可以用红黑树来保证对数级别的性能，找到所有相交区间的复杂度是 RlogN，就一共有 R 个相交的区间这样。

retangle intersection

最后，把二维下的处理对象也升级为矩形，希望知道平面上矩形相交的个数。课程说这个有实际的需求，大概是用来检查电路板之类的，因为摩尔定律啊，平方级别的算法肯定是不行的。

算法和检查二维线段相交差不多，然后这边假定 x，y 坐标不重复。

类似的变成一维上的区间相交检测，在 N 个矩形查找 R 个相交的复杂度是 NlogN + RlogN。

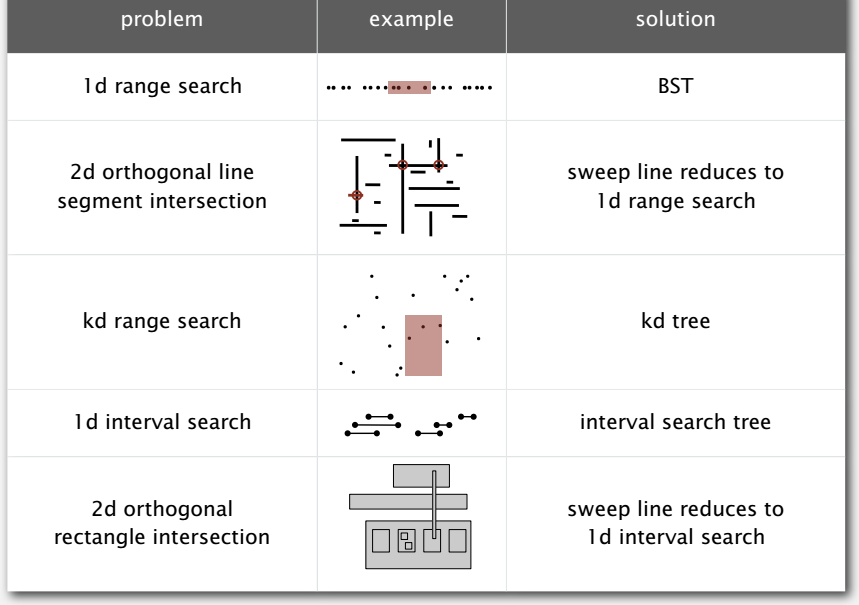
最后的最后，贴张归纳：