堆排序的C++代码实现

堆排序C++实现

堆排序的具体思路可以查看《算法导论》这本书，一下只提供笔者的C++实现代码，并且将笔者在编写程序的过程当中所遇到的一些细节问题拿出来作一番解释，希望能够对对堆排序有一个透彻的理解。

1、构造一个维护堆性质（最大堆）的函数

这里需要做一个假设：对于数组中下标为i的节点其左子树和右子树都是保持最大堆性质的堆。在假设成立的前提上，经过这一个维护函数维护过的堆才能够保证是一个最大堆。函数的C++实现代码如下：

 //假定对某一个节点i其左，右子树都是都是最大堆，但是对于节点i和它的左右子节点则可能破坏最大堆的性质，我们来写一个函数对这
 //情况下的堆来进行维护使整体的堆满足最大堆性质
 void MaxHeapify(int* a,int i,int low,int high)//输入为要被排序的数组和根节点，数组a当中被维护的那一部分的下标low，high
 {
     int l = left(i);//计算下标为i的节点的左子节点
     int r = right(i);//计算下标为i的节点的右子节点
     int largest;//保存i,l,r(即i和它的左右子节点)之间的最大数的下标
     int temp;//交互数组中的数所使用的临时变量
     //找到三个数当中最大的那个数，将最大的那个数和i进行互换
     if (l<=high && a[l]>a[i])
     {
         largest = l;
     }
     else{
         largest = i;
     }

     if (r<=high && a[r]>a[largest])
     {
         largest = r;
     }
     if (largest != i)
     {
         temp = a[i];
         a[i] = a[largest];
         a[largest] = temp;
         MaxHeapify(a, largest,low,high);//交换有可能破坏子树的最大堆性质，所以对所交换的那个子节点进行一次维护，而未交换的那个子节点，根据我们的假设，是保持着最大堆性质的。
     }
 }

代码中还有一个细节需要注意：

 //定义两个有参宏来寻找数组中的数之间的关系
 #define left(x) 2*x+1;//获得左节点在数组中的下标
 #define right(x) 2*(x+1);//获得右节点在数组中的下标

《算法导论》一书当中的数组都是以1作为起始下标的，所以书中计算左右节点的下标的公式分别为：2*i,2*i+1。但是在C++的程序当中数组都是从0开始的所以我们的计算方式也要进行修改。

建堆函数

这个函数负责将数组中元素的位置进行更改保证数组能够构造成为一个最大堆，实现如下：

//将数组建立为一个最大堆
//调整数组当中数的位置将其处理为一个最大堆
void BuildMaxHeap(int* a,int length)
{
    for (int i = length / 2-1; i >= ; i--)
    {
        MaxHeapify(a, i, , length - );
    }
}

其中MaxHeapify函数为在上文中创建的函数。有一个细节的位置和《算法导论》上面的不一样，i=length/2-1，这也是因为数组的起始下标为0所导致的。可以这样理解此处的减1，相当于在以1为起始的数组当中找到这个点之后，对数组整体进行向后位移一个单位就可以得到现在这个点的下标了。

在本节后面的习题当中有提到这么一个问题：为什么是从length/2-1递减到0，而不是从0开始递增到length/2-1呢？从length/2-1递减到0就意味着，从最后的一个非叶节点开始“从小到大”地进行维护，保证每一个点的子树都是最大堆，可以确保最大堆的性质，而如果从0递增到length/2-1则无法保证堆的性质，可以看如下反例：

对数组{14,10,8,16,7}从0递增到length/2-1的堆创建过程如下图所示：

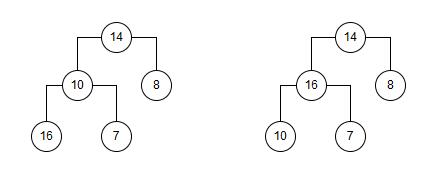可见无法保证最大堆性质。

堆排序函数

实现程序如下：

 //堆排序函数
 void HeapSort(int a[],int length)
 {
     int temp;
     BuildMaxHeap(a,length);
     for (int i = length - ; i >= ; i--)
     {
         //交换根节点和数组的最后一个节点
         temp = a[i];
         a[i] = a[];
         a[] = temp;
         MaxHeapify(a, , , i-);//维护从下标为i-1到0的子数组
     }
 }

在缩减被排列数组这一思路上面我采用的方法是在函数当中输入被排序数组的下标范围。