Bzoj4558:分类讨论 计算几何 组合数学

国际惯例的题面:

这题让我爆肝啦......
这种计数显然容斥，正好不含任何坏点的我们不会算，但是我们能算至少含零个坏点的，至少含一个坏点的，至少含两个坏点的......
所以最终的答案就是(至少含零个坏点的-至少含一个坏点的+至少含两个坏点的-至少含三个坏点的+至少含四个坏点的)。
然后就是怎么计算的问题。
对于至少含零个坏点的，我们不妨设定所有点都是好点。
对于非正放的正方形，我们能找到一个正好包含它的最小的正放的正方形，显然这样的正方形是唯一的。

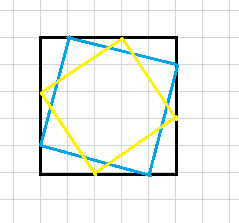
然后我们让四个点在这个正方形的边上滑动，显然这四个点的每一组位置对应一个非正放的正方形(虽然正好在四个角上的是正放的)。
于是我们可以得出总方案数为sigma( i from 1 to min(n,m) ) i * ( n - i + 1 ) * ( m - i + 1 ) 。
这个东西可以O(n)计算。

对于正好有一个坏点的，我们考虑某个以某个个点P为角的正方形A，点P一定包含这个正方形A的最小正放正方形的角上或边上。

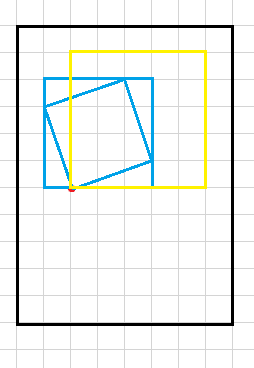
于是我们枚举这样的正方形和点P能在的位置数量就好了。
对于点P的状态，我们计算出它距离左边界的距离l，右边界距离r，上边界距离h。

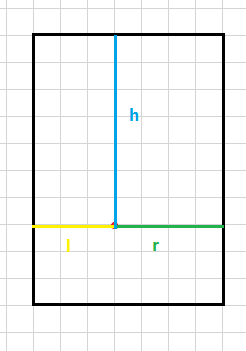
然后我们令t=min(l+r,h)。
如果我们不考虑有一些位置不能取到的话，答案应该为t*(t+3)/2。
然而这样计算了一些不能取到的位置。当t>l时，我们多计算的位置数量为(t-l)*(t-l+1)/2。(手玩一下就明白了)
t>r时同理。这样我们就能O(k)计算出至少含一个坏点的方案数。

对于正好含两及以上个坏点的，我们枚举两个坏点，显然一个正方形给你两个点，他的位置就基本确定了。

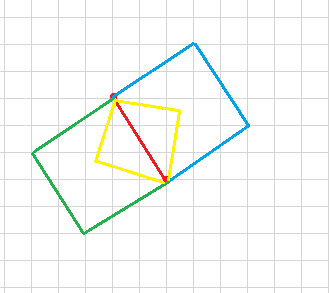
我们可以分类讨论三种情况，用向量计算出另外两个点应该在的位置。注意某些情况下以这两个点为对角线的正方形可能不在格点上。
然后对于含两个的，我们直接计算可行的正方形数；对于含三个的，我们当另外两个点有一个为坏点时计算；含四个的，我们当另外两个点均为坏点时计算。
显然含三个和含四个的我们算重了。所以应该分别除以C(3,2)和C(4,2)。

然后累加一下答案就好。
(然而计算垂直向量时没有加负号让我调了半天，老年选手身败名裂)
代码:

 #include<cstdio>
 #include<algorithm>
 #include<tr1/unordered_set>
 using namespace std;
 using namespace tr1;
 typedef long long int lli;
 using namespace std;
 using namespace tr1;
 const int maxp=2e3+1e2;
 const int mod=1e8+;

 struct Point {
     int x,y;
     friend bool operator < (const Point &a,const Point &b) {
         return a.x != b.x ? a.x < b.x : a.y < b.y;
     }
     friend Point operator - (const Point &a,const Point &b) {
         return (Point){a.x-b.x,a.y-b.y};
     }
     friend Point operator + (const Point &a,const Point &b) {
         return (Point){a.x+b.x,a.y+b.y};
     }
     friend Point operator * (const Point &a,const int &b) {
         return (Point){a.x*b,a.y*b};
     }
     friend Point operator / (const Point &a,const int &b) {
         return (Point){a.x/b,a.y/b};
     }
     inline Point swp() const {
         return (Point){y,-x};
     }
     inline bool candiv() const {
         return ( ! ( x &  ) ) && ( ! ( y &  ) );
     }
 }pt[maxp];
 unordered_set<lli> st;
 int n,m,t;
 lli ans,ini,sig,dou,tri,qua;

 inline void insert(const Point &p) {
     lli h = (lli) p.x * ( m +  ) + p.y;
     st.insert(h);
 }
 inline bool inside(const Point &p) {
     return  <= p.x && p.x <= n &&  <= p.y && p.y <= m;
 }
 inline bool legal(const Point &pa,const Point &pb) {
     return inside(pa) && inside(pb);
 }
 inline bool have(const Point &p) {
     lli h = (lli) p.x * ( m +  ) + p.y;
     return st.find(h) != st.end();
 }
 inline lli calcini(lli n,lli m) {
     lli ret =  , lim = min( n , m );
     for(lli i=;i<=lim;i++) ret = ( ret + ( n - i +  ) % mod * ( m - i +  ) % mod * i % mod ) % mod;
     return ret;
 }
 inline lli calcedge(const lli &l,const lli &r,const lli &h) {
     lli t = min( l + r , h );
     if( !t ) return ;
     lli ret = ( t * ( t +  ) >>  ) % mod;
     if( t > l ) ret -= ( ( t - l ) * ( t - l +  ) >>  ) % mod;
     if( t > r ) ret -= ( ( t - r ) * ( t - r +  ) >>  ) % mod;
     return ( ret % mod + mod ) % mod;
 }
 inline lli calcsingle(lli x,lli y) {
     const lli a = n - x , b = m - y , c = x , d = y;
     lli ret = ( calcedge(d,b,a) + calcedge(d,b,c) + calcedge(a,c,b) + calcedge(a,c,d) ) % mod;
     ret -= ( min(a,b) + min(b,c) + min(c,d) + min(d,a) ) % mod;
     return ( ret % mod + mod ) % mod;
 }
 inline lli calcdouble(const Point &a,const Point &b) {
     const Point delta = (a-b).swp();
     int ret = legal(a+delta,b+delta) + legal(a-delta,b-delta);
     const Point mid = a + b , pa = mid + delta , pb = mid - delta;
     if( pa.candiv() && pb.candiv() && legal(pa/,pb/) ) ++ret;
     return ret;
 }
 inline lli calctriple(const Point &a,const Point &b) {
     const Point delta = (a-b).swp();
     int ret = ;
     if( legal(a+delta,b+delta) ) ret += have(a+delta) + have(b+delta);
     if( legal(a-delta,b-delta) ) ret += have(a-delta) + have(b-delta);
     const Point mid = a + b , pa = mid + delta , pb = mid - delta;
     if( pa.candiv() && pb.candiv() && legal(pa/,pb/) ) ret += have(pa/) + have(pb/);
     return ret;
 }
 inline lli calcquad(const Point &a,const Point &b) {
     const Point delta = (a-b).swp();
     int ret = ;
     if( legal(a+delta,b+delta) ) ret += ( have(a+delta) && have(b+delta) );
     if( legal(a-delta,b-delta) ) ret += ( have(a-delta) && have(b-delta) );
     const Point mid = a + b , pa = mid + delta , pb = mid - delta;
     if( pa.candiv() && pb.candiv() && legal(pa/,pb/) ) ret += ( have(pa/) && have(pb/) );
     return ret;
 }

 int main() {
     scanf("%d%d%d",&n,&m,&t);
     for(int i=;i<=t;i++) scanf("%d%d",&pt[i].x,&pt[i].y) , insert(pt[i]);
     ini = calcini(n,m);
     for(int i=;i<=t;i++) sig += calcsingle(pt[i].x,pt[i].y);
     for(int i=;i<=t;i++) for(int j=i+;j<=t;j++) {
         dou += calcdouble(pt[i],pt[j]) , tri += calctriple(pt[i],pt[j]) , qua += calcquad(pt[i],pt[j]);
     }
     tri /=  , qua /= ;
     ans = ( ( ini - sig + dou - tri + qua ) % mod + mod ) % mod;
     printf("%lld\n",ans);
     return ;
 }