第八集：魔法阵 NTT求循环卷积

题目来源：http://www.fjutacm.com/Problem.jsp?pid=3283

题意：给两串长度为n的数组a和b，视为环，a和b可以在任意位置开始互相匹配得到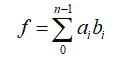这个函数的值，求这个函数的值最大是多少；

很明显是FFT，但是数据范围是n是1e5，a[i]和b[i]是1e6；精度会丢很多，也就是要NTT解决，那么要选一个不会影响答案的P，因为最大值为1e5*1e6*1e6；那么我们选一个1e17以上的就差不多了，然后就是求循环卷积的步骤，对此，我建议你们算一下这个，[a1、a2、a3、a1、a2、a3]*[b1、b2、b3]，列出全部结果(乘法一样的操作，注意每一位乘法的偏移位置)，你会发现得到的新集合去掉头上n-1个以及尾部n-1个就可以得到全部的线性卷积组合，那么我们就可以求那个两个数组的卷积得到的数组里直接找最大：

 #include<stdio.h>
 #include<stdlib.h>
 #include<string.h>
 #include<algorithm>
 using namespace std;
 typedef long long ll;
 const ll PMOD=(27ll<<)+, PR=;
 const int N=1e6+;
 static ll qp[];
 ll res[N];
 inline ll Mul(ll a,ll b){
     if(a>=PMOD)a%=PMOD;
     if(b>=PMOD)b%=PMOD;
     return (a*b-(ll)(a/(long double)PMOD*b+1e-)*PMOD+PMOD)%PMOD;
 }
 struct NTT__container{
     NTT__container( ){
         int  t,i;
         for( i=; i<; i++){///注意循环上界与2n次幂上界相同
             t=<<i;
             qp[i]=quick_pow(PR,(PMOD-)/t);
         }
     }
     ll quick_pow(ll x,ll n){
         ll ans=;
         while(n){
             if(n&)
                 ans=Mul(ans,x);
             x=Mul(x,x);
             n>>=;
         }
         return ans;
     }
     int get_len(int n){///计算刚好比n大的2的N次幂
         int i,len;
         for(i=(<<); i; i>>=){
             if(n&i){
                 len=(i<<);
                 break;
             }
         }
         return len;
     }
     inline void NTT(ll F[],int len,int type){
         int id=,h,j,k,t,i;
         ll E,u,v;
         for(i=,t=; i<len; i++){///逆位置换
             if(i>t)    swap(F[i],F[t]);
             for(j=(len>>); (t^=j)<j; j>>=);
         }
         for( h=; h<=len; h<<=){///层数
             id++;
             for( j=; j<len; j+=h){///遍历这层上的结点
                 E=;///旋转因子
                 for(int k=j; k<j+h/; k++){///遍历结点上的前半序列
                     u=F[k];///A[0]
                     v=Mul(E,F[k+h/]);///w*A[1]
                     ///对偶计算
                     F[k]=(u+v)%PMOD;
                     F[k+h/]=((u-v)%PMOD+PMOD)%PMOD;
                     ///迭代旋转因子
                     E=Mul(E,qp[id]);///qp[id]是2^i等分因子
                 }
             }
         }
         if(type==-){
             int i;
             ll inv;
             for(i=; i<len/; i++)///转置，因为逆变换时大家互乘了对立点的因子
                 swap(F[i],F[len-i]);
             inv=quick_pow(len,PMOD-);///乘逆元还原
             for( i=; i<len; i++)
                 F[i]=Mul(F[i],inv);
         }
     }
     void mul(ll x[],ll y[],int len){///答案存在x中
         int i;
         NTT(x,len,);///先变换到点值式
         NTT(y,len,);///先变换到点值式上
         for(i=; i<len; i++)
             x[i]=Mul(x[i],y[i]);///在点值上点积
         NTT(x,len,-);///再逆变换回系数式
     }
 } cal;
 ll a[N], b[N];
 int main() {
     int n;
     scanf("%d",&n);
     for(int i=;i<n;i++)
         scanf("%lld",a+i), a[i+n]=a[i];
     for(int i=;i<n;i++)
         scanf("%lld",&b[n--i]);
     int len=cal.get_len(n+n+n);
     cal.mul(a, b, len);
     ll mx=;
     for(int i=;i<len;i++){///完整的组合肯定更大所以说直接找最大
         if(mx<a[i]){
             mx=a[i];
         }
     }
     printf("%lld\n",mx);
     return ;
 }

时间：1036MS 内存： 23632KB

还有优化的解法，这我真不知道为什么，可能是因为前后相加刚好可以组合出全部组合：

 #include<stdio.h>
 #include<stdlib.h>
 #include<string.h>
 #include<algorithm>
 using namespace std;
 typedef long long ll;
 const ll PMOD=(27ll<<)+, PR=;
 const int N=1e6+;
 static ll qp[];
 ll res[N];
 inline ll Mul(ll a,ll b){
     if(a>=PMOD)a%=PMOD;
     if(b>=PMOD)b%=PMOD;
     //if(n<=1000000000)return a*b%n;
     return (a*b-(ll)(a/(long double)PMOD*b+1e-)*PMOD+PMOD)%PMOD;
 }
 struct NTT__container{
     NTT__container( ){
         int  t,i;
         for(i=; i<; i++){///注意循环上界与2n次幂上界相同
             t=<<i;
             qp[i]=quick_pow(PR,(PMOD-)/t);
         }
     }
     ll quick_pow(ll x,ll n){
         ll ans=;
         while(n){
             if(n&)
                 ans=Mul(ans,x);
             x=Mul(x,x);
             n>>=;
         }
         return ans;
     }
     int get_len(const int &n){///计算刚好比n大的2的N次幂
         int i, len;
         for(i=(<<); i; i>>=){
             if(n&i){
                 len=(i<<);break;
             }
         }
         return len;
     }
     inline void NTT(ll F[], const int &len, int type){
         int id=, h, j, t, i;
         ll E,u,v;
         for(i=,t=; i<len; i++){///逆位置换
             if(i>t)    swap(F[i],F[t]);
             for(j=(len>>); (t^=j)<j; j>>=);
         }
         for( h=; h<=len; h<<=){///层数
             id++;
             for( j=; j<len; j+=h){///遍历这层上的结点
                 E=;///旋转因子
                 for(int k=j; k<j+h/; k++){///遍历结点上的前半序列
                     u=F[k];///A[0]
                     v=Mul(E,F[k+h/]);///w*A[1]
                     ///对偶计算
                     F[k]=(u+v)%PMOD;
                     F[k+h/]=((u-v)%PMOD+PMOD)%PMOD;
                     ///迭代旋转因子
                     E=Mul(E,qp[id]);///qp[id]是2^i等分因子
                 }
             }
         }
         if(type==-){
             int i;
             ll inv;
             for(i=; i<len/; i++)///转置，因为逆变换时大家互乘了对立点的因子
                 swap(F[i],F[len-i]);
             inv=quick_pow(len,PMOD-);///乘逆元还原
             for( i=; i<len; i++)
                 F[i]=Mul(F[i],inv);
         }
     }
     void mul(ll x[],ll y[],int len){///答案存在x中
         int i;
         NTT(x,len,);///先变换到点值式
         NTT(y,len,);///先变换到点值式上
         for(i=; i<len; i++)
             x[i]=Mul(x[i],y[i]);///在点值上点积
         NTT(x,len,-);///再逆变换回系数式
     }
 } cal;
 ll a[N], b[N];
 int main() {
     int n;
     scanf("%d",&n);
     for(int i=;i<n;i++)
         scanf("%lld",a+i);
     for(int i=;i<n;i++)
         scanf("%lld",&b[n--i]);
     int len=cal.get_len(n+n);
     cal.mul(a, b, len);
     ll mx=;
     for(int i=;i<len;i++){
         a[i]+=a[i+n];
         if(mx<a[i]){
             mx=a[i];
         }
     }
     printf("%lld\n",mx);
     return ;
 }

时间：560MS 内存：23632KB