图-图的表示、搜索算法及其Java实现

1.图的表示方法

图：G=(V,E)，V代表节点，E代表边。

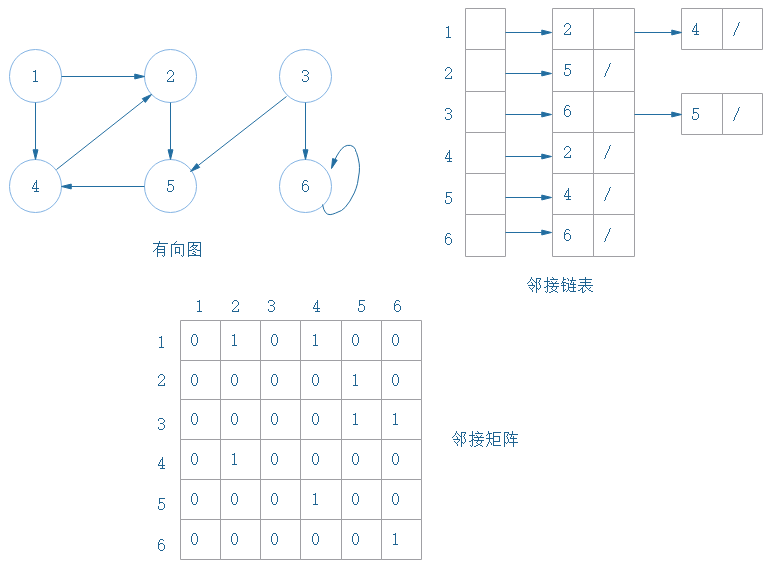
图有两种表示方法：邻接链表和邻接矩阵

邻接链表因为在表示稀疏图（边的条数|E|远远小于|V|²的图）时非常紧凑而成为通常的选择。

如果需要快速判断任意两个节点之间是否有边相连，可能也需要使用邻接矩阵表示法。

邻接链表表示法的鲁棒性很高，可以对其进行简单修改来支持许多其他的图变种。

邻接链表的一个潜在缺陷是无法快速判断一条边是否是图中地一条边。邻接矩阵则克服了这个缺陷，但付出的代价是更大的存储空间消耗。

——摘自《算法导论》

（1）无向图的两种表示

（2）有向图的两种表示

2.图的搜索算法

图的搜索算法即：广度优先搜索和深度优先搜索

相信这两种搜索算法的基本概念根据名字就可窥得一二，不多说，直接上例子。

如上有向图，创建三个类：

• 点Vertex：包括点的名称（String）和访问标志（boolean）。
• 边Edge：包括前驱点（Vertex）和后继点（Vertex）。
• 图Graph：包括点集合（ArrayList<Vertex>）和边集合（ArrayList<Edge>）。

以下是构建好的图信息以及点遍历结果。

以下是Java源码。BFS辅以队列以非递归方法完成，DFS以递归方法完成。注释得很详细，我就不多解释了@(^<>^)@。

 import java.util.ArrayList;
 import java.util.Iterator;
 import java.util.LinkedList;
 import java.util.Queue;

 class Graph{
     ArrayList<Vertex> vertexs=new ArrayList<Vertex>();
     ArrayList<Edge> edges=new ArrayList<Edge>();

     public void addVertex(Vertex vertex) {
         vertexs.add(vertex);
     }

     public void addEdge(Edge edge) {
         edges.add(edge);
     }
 }

 //顶点类
 class Vertex{
     String name;
     boolean visited=false;     //标记该点是否被查看-广度优先专用
     boolean visited2=false;     //标记该点是否被查看-深度优先专用

     public Vertex(String name) {
         this.name=name;
     }

     @Override
     public String toString() {
         return "[" + name + "]";
     }
 }
 //边类 有向图
 class Edge{
     Vertex start;
     Vertex end;

     public Edge(Vertex start,Vertex end) {
         this.start=start;
         this.end=end;
     }

     @Override
     public String toString() {
         return "(" + start + "," + end + ")";
     }
 }

 public class SearchGraph {
     //广度优先 非递归
     static void BFS(Graph graph) {
         ArrayList<Vertex> vertexs=graph.vertexs;
         ArrayList<Edge> edges=graph.edges;
         Queue<Vertex> queue = new LinkedList<Vertex>();   //创建队列

         queue.add(vertexs.get(0));    //顶节点放入队列
         vertexs.get(0).visited=true;      //顶节点设为已阅
         System.out.print(vertexs.get(0));

         while(!queue.isEmpty()) {
             Vertex vertex=queue.remove();
             for(Edge edge:edges) {
                 if(edge.start.equals(vertex)&&edge.end.visited==false) {
                     queue.add(edge.end);
                     edge.end.visited=true;
                     System.out.print(edge.end);
                 }
             }
         }

     }

     //深度优先 递归
     static void DFS(Graph graph,Vertex vertex) {  //参数：图、点信息
         System.out.print(vertex);
         vertex.visited2=true;

         for(Edge edge:graph.edges) {
             if(edge.start.equals(vertex)&&edge.end.visited2==false) {
                 DFS(graph,edge.end);
             }
         }
     }

     public static void main(String[] args) {
         // TODO Auto-generated method stub

         //构造有向图
         Graph graph=new Graph();
         Vertex v0=new Vertex("v0");
         Vertex v1=new Vertex("v1");
         Vertex v2=new Vertex("v2");
         Vertex v3=new Vertex("v3");
         Vertex v4=new Vertex("v4");
         Vertex v5=new Vertex("v5");
         Vertex v6=new Vertex("v6");
         graph.addVertex(v0);
         graph.addVertex(v1);
         graph.addVertex(v2);
         graph.addVertex(v3);
         graph.addVertex(v4);
         graph.addVertex(v5);
         graph.addVertex(v6);
         Edge e0=new Edge(v0,v1);
         Edge e1=new Edge(v0,v2);
         Edge e2=new Edge(v0,v3);
         Edge e3=new Edge(v1,v4);
         Edge e4=new Edge(v1,v5);
         Edge e5=new Edge(v2,v4);
         Edge e6=new Edge(v3,v5);
         Edge e7=new Edge(v4,v6);
         Edge e8=new Edge(v5,v6);
         graph.addEdge(e0);
         graph.addEdge(e1);
         graph.addEdge(e2);
         graph.addEdge(e3);
         graph.addEdge(e4);
         graph.addEdge(e5);
         graph.addEdge(e6);
         graph.addEdge(e7);
         graph.addEdge(e8);
         //构造有向图

         //测试图创建结果
         ArrayList<Vertex> vertexs=graph.vertexs;
         ArrayList<Edge> edges=graph.edges;
         Iterator iVertex=vertexs.iterator();
         Iterator iEdge=edges.iterator();
         System.out.println("点集合：");
         while(iVertex.hasNext()) {
             System.out.print(iVertex.next());
         }
         System.out.println();
         System.out.println("边集合：");
         while(iEdge.hasNext()) {
             System.out.print(iEdge.next());
         }
         //测试图创建结果

         //遍历
         System.out.println("");
         System.out.println("广度优先遍历：");
         BFS(graph);
         System.out.println("");
         System.out.println("深度优先遍历：");
         DFS(graph,v0);
         //遍历
     }

 }