隐马尔科夫模型研究 stock 以及 lotto
说明
本文参考了这里
由于数据是连续的,因此使用了高斯隐马尔科夫模型:gaussianHMM
一、stock代码
import tushare as ts
import pandas as pd
import numpy as np
from hmmlearn.hmm import GaussianHMM
from matplotlib import cm, pyplot as plt
import seaborn as sns
sns.set_style('white')
'''
假定隐藏状态数目为4,观测状态数目为2
'''
# 1.准备 X
df = ts.get_hist_data('sh',start='2014-01-01',end='2017-07-27')[::-1] # 上证指数
close = np.log(df['close'])
low, high = np.log(df['low']), np.log(df['high'])
t = 5
X = pd.concat([close.diff(1), close.diff(t), high-low], axis=1)[t:] # 显状态时间序列(观测得到)
# 2.拟合 HMM
model = GaussianHMM(n_components=6, covariance_type="diag", n_iter=1000).fit(X)
Z = model.predict(X) # 隐状态时间序列
# 3.画图看看
plt.figure(figsize=(12, 7))
for i in range(model.n_components):
mask = (Z==i) # 注意这里的Z!!!
plt.plot_date(df.index[t:][mask], df['close'][t:][mask],'.',label=f'{i}th hidden state',lw=1)
plt.legend()
plt.grid(1)
plt.show()
效果图
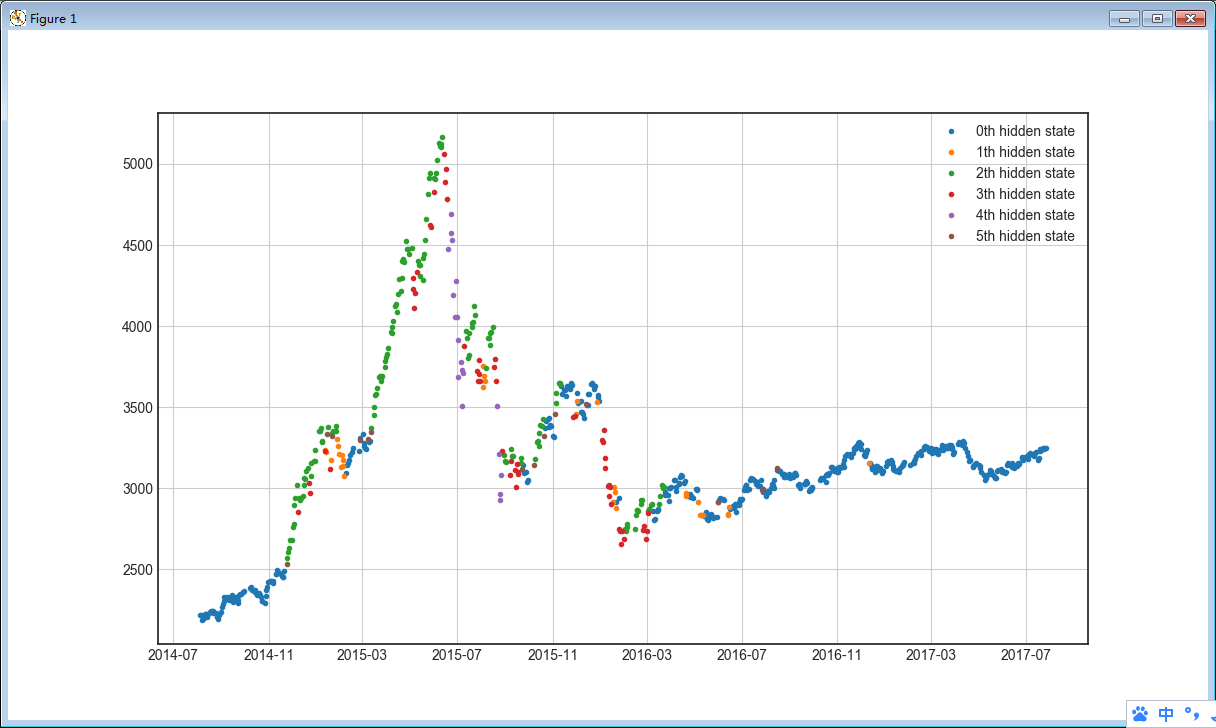
解释
下面是对6种隐状态的一种可能的解释:【图文对不上,文字来自这里】
- 状态0————蓝色————震荡下跌
- 状态1————绿色————小幅的上涨
- 状态2————红色————牛市上涨
- 状态3————紫色————牛市下跌
- 状态4————黄色————震荡下跌
- 状态5————浅蓝色————牛市下跌
以上的意义归结是存在一定主观性的。因为HMM模型对输入的多维度观测变量进行处理后,只负责分出几个类别,而并不会定义出每种类别的实际含义。所以我们从图形中做出上述的判断。
所以,这种方法本质上是一种 Classification(分类) 或者 Clustering(聚类)
二、lotto 代码
import tushare as ts
import pandas as pd
import numpy as np
from hmmlearn.hmm import GaussianHMM
from matplotlib import cm, pyplot as plt
from matplotlib.widgets import MultiCursor
import seaborn as sns
sns.set_style('white')
import marksix_1
import talib as ta
'''
假定隐藏状态数目为6,观测状态数目为4
'''
# 1.准备 X
lt = marksix_1.Marksix()
lt.load_data(period=1000)
#series = lt.adapter(loc='0000001', zb_name='ptsx', args=(1,), tf_n=0)
m = 2
series = lt.adapter(loc='0000001', zb_name='mod', args=(m, lt.get_mod_list(m)), tf_n=0)
# 实时线
close = np.cumsum(series).astype(float)
# 低阶数据
t1, t2, t3 = 5, 10, 20
ma1 = ta.MA(close, timeperiod=t1, matype=0)
std1 = ta.STDDEV(close, timeperiod=t1, nbdev=1)
ma2 = ta.MA(close, timeperiod=t2, matype=0)
std2 = ta.STDDEV(close, timeperiod=t2, nbdev=1)
ma3 = ta.MA(close, timeperiod=t3, matype=0)
std3 = ta.STDDEV(close, timeperiod=t3, nbdev=1)
# 转换一
'''
t = t3
X = pd.DataFrame({'ma1':ma1,'ma2':ma2,'ma3':ma3,'std1':std1,'std2':std2,'std3':std3}, index=lt.df.index)[t:]
'''
# 转换二
t = t2
X = pd.DataFrame({'ma1':ma1,'ma2':ma2,'std1':std1,'std2':std2}, index=lt.df.index)[t:]
#close = np.log(df['close'])
#low, high = np.log(df['low']), np.log(df['high'])
#t = 5
#X = pd.concat([close.diff(1), close.diff(t), high-low], axis=1)[t:] # 显状态时间序列(观测得到)
# 2.拟合 HMM
model = GaussianHMM(n_components=6, covariance_type="diag", n_iter=1000).fit(X)
Z = model.predict(X) # 隐状态时间序列
# 3.画图看看
fig, axes = plt.subplots(2, 1, sharex=True)
ax1, ax2 = axes[0], axes[1]
show_period = 300
# 布林线
upperband, middleband, lowerband = ta.BBANDS(close, timeperiod=5, nbdevup=2, nbdevdn=2, matype=0)
axes[0].plot_date(lt.df.index[-show_period:], close[-show_period:], 'rd-', markersize = 3)
axes[0].plot_date(lt.df.index[-show_period:], upperband[-show_period:], 'y-')
axes[0].plot_date(lt.df.index[-show_period:], middleband[-show_period:], 'b-')
axes[0].plot_date(lt.df.index[-show_period:], lowerband[-show_period:], 'y-')
for i in range(model.n_components):
mask = (Z[-show_period:]==i) # 注意这里的Z!!!
axes[1].plot_date(lt.df.index[-show_period:][mask], close[-show_period:][mask],'d',markersize=3,label=f'{i}th hidden state',lw=1)
axes[1].legend()
axes[1].grid(1)
multi = MultiCursor(fig.canvas, (axes[0], axes[1]), color='b', lw=2)
plt.show()
效果图
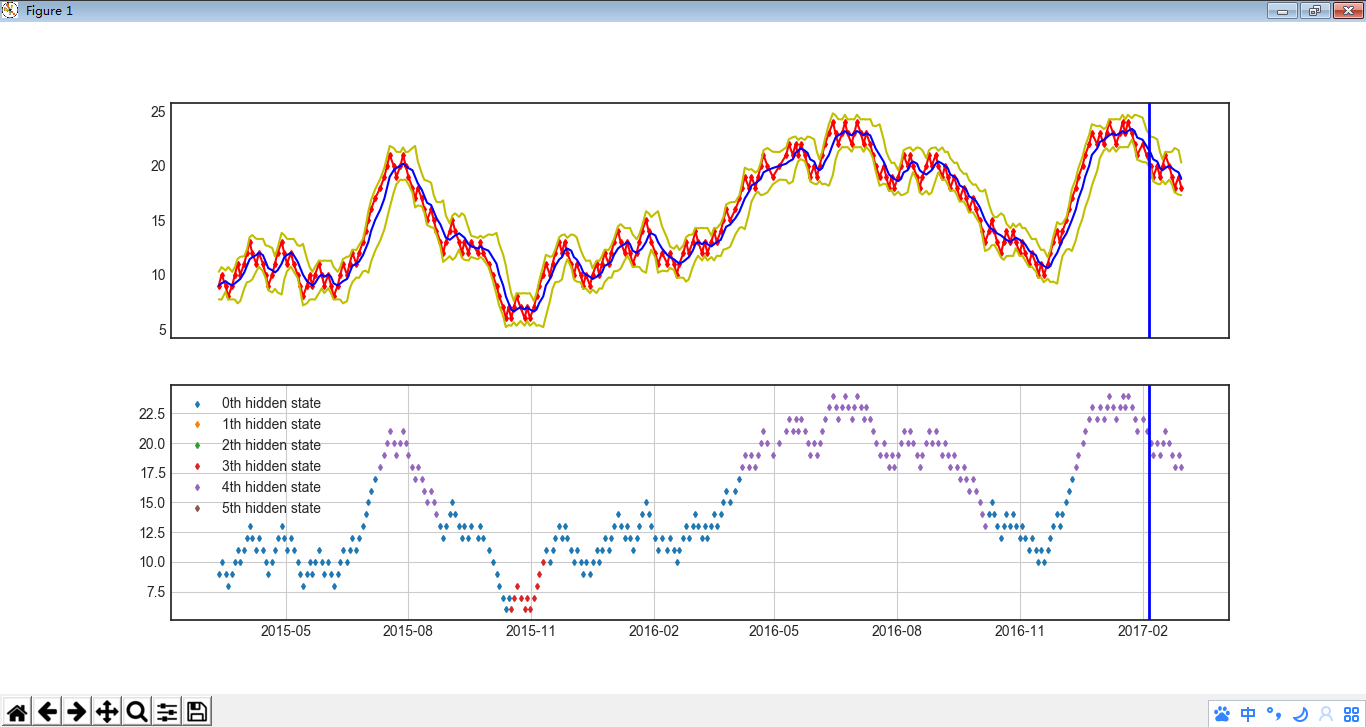
隐马尔科夫模型研究 stock 以及 lotto的更多相关文章
- HMM基本原理及其实现(隐马尔科夫模型)
HMM(隐马尔科夫模型)基本原理及其实现 HMM基本原理 Markov链:如果一个过程的“将来”仅依赖“现在”而不依赖“过去”,则此过程具有马尔可夫性,或称此过程为马尔可夫过程.马尔可夫链是时间和状态 ...
- 基于隐马尔科夫模型(HMM)的地图匹配(Map-Matching)算法
文章目录 1. 1. 摘要 2. 2. Map-Matching(MM)问题 3. 3. 隐马尔科夫模型(HMM) 3.1. 3.1. HMM简述 3.2. 3.2. 基于HMM的Map-Matchi ...
- 隐马尔科夫模型HMM学习最佳范例
谷歌路过这个专门介绍HMM及其相关算法的主页:http://rrurl.cn/vAgKhh 里面图文并茂动感十足,写得通俗易懂,可以说是介绍HMM很好的范例了.一个名为52nlp的博主(google ...
- 隐马尔科夫模型HMM(三)鲍姆-韦尔奇算法求解HMM参数
隐马尔科夫模型HMM(一)HMM模型 隐马尔科夫模型HMM(二)前向后向算法评估观察序列概率 隐马尔科夫模型HMM(三)鲍姆-韦尔奇算法求解HMM参数(TODO) 隐马尔科夫模型HMM(四)维特比算法 ...
- 隐马尔科夫模型(Hidden Markov Models)
链接汇总 http://www.csie.ntnu.edu.tw/~u91029/HiddenMarkovModel.html 演算法笔记 http://read.pudn.com/downloads ...
- 隐马尔科夫模型HMM
崔晓源 翻译 我们通常都习惯寻找一个事物在一段时间里的变化规律.在很多领域我们都希望找到这个规律,比如计算机中的指令顺序,句子中的词顺序和语音中的词顺序等等.一个最适用的例子就是天气的预测. 首先,本 ...
- 隐马尔科夫模型(HMM)
基本概念 1Markov Models 2Hidden Markov Models 3概率计算算法前向后向算法 1-3-1直接计算 1-3-2前向算法 1-3-3后向算法 4学习问题Baum-Welc ...
- 机器学习中的隐马尔科夫模型(HMM)详解
机器学习中的隐马尔科夫模型(HMM)详解 在之前介绍贝叶斯网络的博文中,我们已经讨论过概率图模型(PGM)的概念了.Russell等在文献[1]中指出:"在统计学中,图模型这个术语指包含贝叶 ...
- 隐马尔科夫模型 HMM(Hidden Markov Model)
本科阶段学了三四遍的HMM,机器学习课,自然语言处理课,中文信息处理课:如今学研究生的自然语言处理,又碰见了这个老熟人: 虽多次碰到,但总觉得一知半解,对其了解不够全面,借着这次的机会,我想要直接搞定 ...
随机推荐
- 腾讯云Centos安装jdk8
1.下载jdk1.8的tar cd /usr/local/src #切换到该目录下 wget url #下载jdk8的tar包 2.下载完成后解压tar包 tar -zxvf jdk-8u152-li ...
- JavaScript动画:offset和匀速动画详解(含轮播图的实现)
本文最初发表于博客园,并在GitHub上持续更新前端的系列文章.欢迎在GitHub上关注我,一起入门和进阶前端. 以下是正文. offset简介 我们知道,三大家族包括:offset/scroll/c ...
- 无法将数据库从SINGLE_USER模式切换回MULTI_USER模式(Error 5064),及查找SQL Server数据库中用户spid(非SQL Server系统spid)的方法
今天公司SQL Server数据库无意间变为SINGLE_USER模式了,而且使用如下语句切换回MULTI_USER失败: ALTER DATABASE [MyDB] SET MULTI_USER W ...
- Lorem 占位符
Web开发者通常用lorem ipsum text来做占位符,占位符就是占着位置的一些文字,没有实际意义. 为什么叫lorem ipsum text呢? 是因为lorem ipsum是古罗马西塞罗谚语 ...
- python 多进程 Event的使用
Event事件 多进程的使用 通俗点儿讲 就是 1. Event().wait() 插入在进程中插入一个标记(flag) 默认为 false 然后flag为false时 程序会停止运 ...
- xml 注意事项
<?xml version="1.0" encoding="GB2312"?> xml区分大小写,只能有一个根元素,属性值必须放在引号中,空格不 ...
- 【转】Java学习---JDK、JRE和JVM的关系
[原文]https://www.toutiao.com/i6591348937267872269/ 首先是JDK JDK(Java Development Kit) 是 Java 语言的软件开发工具包 ...
- tidb导入大量数据报错:statement count 5001 exceeds the transaction limitation, autocommit = false
这是Tidb数据库事务提交数量达到上限的一种报错:因为tidb是分布式的数据库,tikv使用了底层的强一致性协议.这是分布式数据库必然遇到的一个问题,我们可以调整这个值:在tidb的配置文件里面“st ...
- 安装Tidb数据库出现SSD硬盘IOPS不到40000的错误
今天安装tidb数据库出现IOPS过低的问题,这里如果仅仅是测试的话我们可以降低这个值,大概遇到的问题是: 解决方法: 1.我们在中控机的目录下修改某个配置文件: [tidb@:vg_adn_tidb ...
- 使用TuShare下载历史逐笔成交数据并生成1分钟线
使用如下代码从TuShare下载沪深300每只股票的历史成交记录并按股票.日期保存到本地.主要是为了以后查询方便快速. #-*- coding: utf-8 -*- import numpy as n ...
