【C#数据结构系列】线性表

一：线性表

1.1：定义：零个或多个数据元素的有限序列

1.2：

　　线性表元素个数n定义为线性表的长度，n = 0称为空表，i 为数据元素ai在线性表中的位序。

1.3：满足线性表的条件：（1）：有序，有限

　　　　　　　　　　  （2）：第一个元素无前驱，最后一个元素无后继

　　　　　　　　　　  （3）：数据类型相同

　　　　　　　　　　  （4）：元素之间首位相连

1.4：线性表两种存储结构：顺序存储结构和链式存储结构

二：线性表顺序存储结构

2.1：顺序存储（Sequence Storage）结构定义：指的是用一段地址连续的存储单元依次存储线性表的数据元素。

2.2：数据长度和线性表长度的区别：数组长度是存放线性表的存储空间的长度，一般不变。线性表长度是线性表中数据元素的个数，会随着插入和删除而改变。

2.3：线性表常用操作接口：

 public interface IListDS<T>
     {
         int GetLength(); //求长度
         void Clear(); //清空操作
         bool IsEmpty(); //判断线性表是否为空
         void Append(T item); //附加操作
         void Insert(T item, int i); //插入操作
         T Delete(int i); //删除操作
         T GetElem(int i); //取表元
         int Locate(T value); //按值查找

     }

2.4：顺序表实现：类 SeqList<T>的实现说明如下

     /// <summary>
     /// 线性表的顺序存储结构
     /// </summary>
     /// <typeparam name="T"></typeparam>
     public class SeqList<T> : IListDS<T>
     {
         private int maxsize;//顺序表的容量
         private T[] data;//数组，用于存储顺序表中的数据元素
         private int last;//指示顺序表最后一个元素的位置

         //索引器
         public T this[int index]
         {
             get
             {
                 return data[index];
             }
             set
             {
                 data[index] = value;
             }
         }

         //最后一个数据元素位置属性
         public int Last
         {
             get
             {
                 return last;
             }
         }

         //容量属性
         public int MaxSize
         {
             get
             {
                 return maxsize;
             }
             set
             {
                 maxsize = value;
             }
         }

         //构造器
         public SeqList(int size)
         {
             data = new T[size];
             maxsize = size;
             last = -;
         }

         //求顺序表的长度
         public int GetLength()
         {
             return last + ;
         }

         //清空顺序表
         public void Clear()
         {
             last = -;
         }

         //判断顺序表是否为空
         public bool IsEmpty()
         {
             if (last == -)
             {
                 return true;
             }
             else
             {
                 return false;
             }
         }

         //判断顺序表是否为满
         public bool IsFull()
         {
             if (last == maxsize - )
             {
                 return true;
             }
             else
             {
                 return false;
             }
         }

         public void Append(T item)
         {
             if (IsFull())
             {
                 Console.WriteLine("List is full");
                 return;
             }
             data[++last] = item;
         }

         //在顺序表的第i个数据元素的位置插入一个数据元素
         public void Insert(T item, int i)
         {
             if (IsFull())
             {
                 Console.WriteLine("List is full");
                 return;
             }

             if (i <  || i > last + )
             {
                 Console.WriteLine("Position is error!");
                 return;
             }

             if (i == last + )//在末尾插入
             {
                 data[last + ] = item;
             }
             else
             {
                 for (int k = last; k >= i - ; --k)
                 {
                     data[k + ] = data[k];
                 }
                 data[i - ] = item;
             }
             ++last;//最后一个元素的位置加一
         }

         //删除顺序表的第i个数据元素,返回删除元素
         public T Delete(int i)
         {
             T tmp = default(T);
             if (IsEmpty())
             {
                 Console.WriteLine("List is empty");
                 return tmp;
             }
             if (i <  || i > last + )
             {
                 Console.WriteLine("Position is error!");
                 return tmp;
             }
             if (i == last + )//末尾删除
             {
                 tmp = data[last--];
             }
             else
             {
                 tmp = data[i - ];
                 for (int k = i; k <= last; ++k)
                 {
                     data[k - ] = data[k];
                 }
             }
             --last;
             return tmp;
         }

         //获得顺序表的第i个数据元素
         public T GetElem(int i)
         {
             if (IsEmpty() || (i < ) || (i > last + ))
             {
                 Console.WriteLine("List is empty or Position is error!");
                 return default(T);
             }
             return data[i - ];
         }

         //在顺序表中查找值为value的数据元素
         public int Locate(T value)
         {
             if (IsEmpty())
             {
                 Console.WriteLine("List is Empty!");
                 return -;
             }
             int i = ;
             for (i = ; i <= last; ++i)
             {
                 if (value.Equals(data[i]))
                 {
                     break;
                 }
             }
             if (i > last)
             {
                 return -;
             }
             return i;
         }

     }

2.5：优缺点：

　 优点：  （1）：无须为表示表中之间的逻辑关系而增加额外的存储空间

　　　　   （2）：可以快速的读取表中的任意位置的元素

　 缺点：  （1）：插入和删除操作需要移动大量元素

　　　　   （2）：当线性表长度变化较大时，难以确定存储空间的容量

　　　　   （3）：造成存储空间的"碎片"。

三：线性表的链式存储结构

3.1：链表定义：链表是用一组任意的存储单元来存储线性表中的数据元素（这组存储单元可以是连续的，也可以是不连续的）。

3.2：在存储数据元素时，除了存储数据元素本身的信息外，还要存储与它相邻的数据元素的存储地址信息。这两部分信息组成该数据元素的存储映像(Image)，称为结点(Node)。把存储据元素本身信息的域叫结点的数据域(Data Domain)，把存储与它相邻的数据元素的存储地址信息的域叫结点的引用域(Reference Domain)。

3.3：单链表

3.3.1：如果结点的引用域只存储该结点直接后继结点的存储地址，则该链表叫单链表(Singly Linked List)

3.3.2：单链表的的结点结构如下：

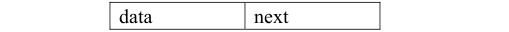
　　把单链表结点看作是一个类，类名为 Node<T>。单链表结点类的实现如下所示。　

     /// <summary>
     /// 单链表节点类实现
     /// </summary>
     /// <typeparam name="T"></typeparam>
     public class Node<T>
     {
         private T data;//数据域
         private Node<T> next;//引用域

         //构造器
         public Node(T val, Node<T> p)
         {
             Data = val;
             Next = p;
         }

         public Node(Node<T> p)
         {
             Next = p;
         }

         public Node(T val)
         {
             Data = val;
             Next = null;
         }

         public Node()
         {
             Data = default(T);
             Next = null;
         }

         public T Data { get; set; }
         public Node<T> Next { get; set; }
     }

3.3.3：通常，我们把链表画成用箭头相连接的结点的序列，结点间的箭头表示引用域中存储的地址。为了处理上的简洁与方便，在本书中把引用域中存储的地址叫引用。单链表示意图如下：

　  

　　由图可知单链表由头引用 H 唯一确定。头引用指向单链表的第一个结点，也就是把单链表第一个结点的地址放在 H 中，所以，H 是一个 Node 类型的变量。头引用为 null 表示一个空表。

3.3.4： 把单链表看作是一个类，类名叫 LinkList<T>。LinkList<T>类也实现了接口IListDS<T>。LinkList<T>类有一个字段 head，表示单链表的头引用，所以 head的类型为 Node<T>。由于链表的存储空间不是连续的，所以没有最大空间的限制，在链表中插入结点时不需要判断链表是否已满。因此，在 LinkList<T>类中不需要实现判断链表是否已满的成员方法。

　　单链表类 LinkList<T>的实现说明如下所示。

     /// <summary>
     /// //单链表类实现
     /// </summary>
     /// <typeparam name="T"></typeparam>
     public class LinkList<T> : IListDS<T>
     {
         private Node<T> head;   //单链表的头引用

         public Node<T> Head //头引用属性
         {
             get
             {
                 return head;
             }
             set
             {
                 head = value;
             }
         }

         public LinkList()
         {
             head = null;
         }

         //求单链表的长度
         public int GetLength()
         {
             Node<T> p = head;
             int length = ;
             while (p != null)
             {

                 ++length;
                 p = p.Next;

             }
             return length;

         }

         //清空单链表
         public void Clear()
         {
             head = null;
         }

         //判断单链表是否为空
         public bool IsEmpty()
         {
             if (head == null)
             {
                 return true;
             }
             else
             {
                 return false;
             }
         }

         //在单链表的末尾(空节点)添加新元素
         public void Append(T item)
         {
             Node<T> q = new Node<T>(item);
             Node<T> p = new Node<T>();//头结点

             if (head == null)
             {
                 head = q;
                 return;
             }

             p = head;
             while (p.Next != null)
             {
                 p = p.Next;
             }

             p.Next = q;
         }

         //在单链表的第i个结点的位置前插入一个值为item的结点
         public void Insert(T item, int i)
         {

             if (IsEmpty() || i < )
             {
                 Console.WriteLine(" List is empty or Position is error! ");
                 return;
             }

             if (i == )
             {
                 Node<T> q = new Node<T>(item);
                 q.Next = head;
                 head = q;
                 return;
             }

             Node<T> p = head;
             Node<T> r = new Node<T>();
             int curPosition = ;

             while (p.Next != null && curPosition < i)
             {
                 r = p;
                 p = p.Next;
                 ++curPosition;
             }

             if (curPosition == i)
             {
                 Node<T> q = new Node<T>(item);
                 q.Next = p;
                 r.Next = q;

             }
         }

         //在单链表的第i个结点的位置后插入一个值为item的结点
         public void InsertPost(T item, int i)
         {
             if (IsEmpty() || i < )
             {
                 Console.WriteLine(" List is empty or Position is error! ");
                 return;
             }

             if (i == )
             {
                 Node<T> q = new Node<T>(item);
                 q.Next = head.Next;
                 head.Next = q;
                 return;
             }

             Node<T> p = head;
             int curPosition = ;

             while (p != null && curPosition < i)
             {
                 p = p.Next;
                 ++curPosition;
             }

             if (curPosition == i)
             {
                 Node<T> q = new Node<T>(item);
                 q.Next = p.Next;
                 p.Next = q;
             }
         }

         //删除单链表的第i个结点
         public T Delete(int i)
         {
             if (IsEmpty() || i < )
             {
                 Console.WriteLine(" List is empty or Position is error! ");
                 return default(T);
             }

             Node<T> q = new Node<T>();

             if (i == )
             {
                 q = head;
                 head = head.Next;
                 return q.Data;
             }

             Node<T> p = head;
             int curPosition = ;
             while (p.Next != null && curPosition < i)
             {
                 q = p;
                 p = p.Next;
                 ++curPosition;
             }

             if (curPosition == i)
             {
                 q.Next = p.Next;
                 return p.Data;
             }
             else
             {
                 Console.WriteLine("The ith node is not exist!");
                 return default(T);
             }

         }

         //获得单链表的第i个数据元素
         public T GetElem(int i)
         {
             if (IsEmpty())
             {
                 Console.WriteLine(" List is empty or Position is error! ");
                 return default(T);
             }

             Node<T> p = new Node<T>();
             p = head;
             int curPosition = ;

             while (p.Next != null && curPosition < i)
             {
                 p = p.Next;
                 ++curPosition;
             }

             if (curPosition == i)
             {
                 return p.Data;
             }
             else
             {
                 Console.WriteLine("The ith node is not exist!");
                 return default(T);
             }
         }

         //在单链表中查找值为value的结点
         public int Locate(T value)
         {
             if (IsEmpty())
             {
                 Console.WriteLine(" List is empty or Position is error! ");
                 return -;
             }

             Node<T> p = new Node<T>();
             p = head;
             int curPosition = ;
             while (!p.Data.Equals(value) && p.Next != null)
             {
                 p = p.Next;
                 ++curPosition;
             }

             return curPosition;
         }
     }

3.3.5： 算法的时间复杂度分析：从前插和后插运算的算法可知，在第 i 个结点处插入结点的时间主要消耗在查找操作上。由上面几个操作可知，单链表的查找需要从头引用开始，一个结点一个结点遍历，因为单链表的存储空间不是连续的空间。这是单链表的缺点，而是顺序表的优点。找到目标结点后的插入操作很简单，不需要进行数据元素的移动，因为单链表不需要连续的空间。删除操作也是如此，这是单链表的优点，相反是顺序表的缺点。遍历的结点数最少为 1 个，当 i 等于1 时，最多为 n，n 为单链表的长度，平均遍历的结点数为 n/2。所以，插入操作的时间复杂度为 O（n）。

　　因此，线性表的顺序存储和链式存储各有优缺点，线性表如何存储取决于使用的场合。如果不需要经常在线性表中进行插入和删除，只是进行查找，那么，线性表应该顺序存储；如果线性表需要经常插入和删除，而不经常进行查找，则线性表应该链式存储。

3.3.6：单链表的建立

　　单链表的建立与顺序表的建立不同，它是一种动态管理的存储结构，链表中的每个结点占用的存储空间不是预先分配，而是运行时系统根据需求而生成的。单链表的建立分为在头部插入结点建立单链表和在尾部插入结点建立单链表。

　　（1）：在单链表的头部插入结点建立单链表。

 //头部插入结点建立单链表的算法如下
         public LinkList<int> CreateLListHead()
         {
             int d;
             LinkList<int> L = new LinkList<int>();
             d = Int32.Parse(Console.ReadLine());
             while (d != -)
             {
                 Node<int> p = new Node<int>(d);
                 p.Next = L.head;
                 L.head = p;
                 d = Int32.Parse(Console.ReadLine());
             }
             return L;
         }

　　（2）：头部插入结点建立单链表简单，但读入的数据元素的顺序与生成的链表中元素的顺序是相反的。若希望次序一致，则用尾部插入的方法。因为每次是将新结点插入到链表的尾部，所以需加入一个引用 R 用来始终指向链表中的尾结点，以便能够将新结点插入到链表的尾部。

 //在尾部插入结点建立单链表的算法如下：
         public LinkList<int> CreateListTail()
         {
             Node<int> R = new Node<int>();
             int d;
             LinkList<int> L = new LinkList<int>();
             R = L.head;//尾部结点
             d = Int32.Parse(Console.ReadLine());
             while (d != -)
             {
                 Node<int> p = new Node<int>(d);
                 if (L.head == null)
                 {
                     L.head = p;
                 }
                 else
                 {
                     R.Next = p;
                 }
                 R = p;
                 d = Int32.Parse(Console.ReadLine());
             }
             if (R != null)
             {
                 R.Next = null;
             }
             return L;
         }

　　（3）：在上面的算法中，第一个结点的处理和其它结点是不同的，原因是第一个结点加入时链表为空，它没有直接前驱结点，它的地址存放在链表的头引用中；而其它结点有直接前驱结点，其地址放在直接前驱结点的引用域中。在头部插入结点建立单链表的算法中，头引用所指向的结点也是变化的。“第一个结点”的问题在很多操作中都会遇到，如前面讲的在链表中插入结点和删除结点。为了方便处理，其解决办法是让头引用保存的结点地址不变。因此，在链表的头部加入了一个叫头结点(Head Node)的结点，把头结点的地址保存在头引用中。这样，即使是空表，头引用变量也不为空。头结点的加入使得“第一个结点”的问题不再存在，也使得“空表”和“非空表”的处理一致。

　　头结点的加入完全是为了操作的方便，它的数据域无定义，引用域存放的是第一个结点的地址，空表时该引用域为空。带头结点的单链表空表和非空表的示意图如下：

　　单链表带头结点和不带头结点，操作有所不同，上面讲的操作都是不带头结点的操作。例如：带头结点的单链表的长度是不带头结点的单链表的长度加 1。在需要遍历单链表时，不带头结点的单链表是把头引用 head 赋给一个结点变量，即 p = head，p 为结点变量;而带头结点的单链表是把 head 的引用域赋给一个结点变量，即 p = head.Next，p 为结点变量。

　　3.4：双向链表

　　3.4.1：在结点中设两个引用域，一个保存直接前驱结点的地址，叫 prev，一个直接后继结点的地址，叫 next，这样的链表就是双向链表(Doubly Linked List)。双向链表的结点结构如下图：

　　

　　双向链表结点的定义与单链表的结点的定义很相似，，只是双向链表多了一个字段 prev。双向链表结点类的实现如下所示

 /// <summary>
     /// 双向链表结点类的实现
     /// </summary>
     /// <typeparam name="T"></typeparam>
     public class DbNode<T>
     {
         private T data;//数据域
         private DbNode<T> prev;////前驱引用域
         private DbNode<T> next;//后继引用域

         //构造器
         public DbNode(T val, DbNode<T> p)
         {
             Data = val;
             Next = p;
         }

         public DbNode(DbNode<T> p)
         {
             Next = p;
         }

         public DbNode(T val)
         {
             Data = val;
             Next = null;
         }

         public DbNode()
         {
             Data = default(T);
             Next = null;
         }

         //数据域属性
         public T Data { get; set; }

         //前驱引用域属性
         public DbNode<T> Prev { get; set; }

         //后继引用域属性
         public DbNode<T> Next { get; set; }

     }

　　3.4.2：双向链表插入：由于双向链表的结点有两个引用，所以，在双向链表中插入和删除结点比单链表要复杂。双向链表中结点的插入分为在结点之前插入和在结点之后插入，插入操作要对四个引用进行操作。下面以在结点之后插入结点为例来说明在双向链表中插入结点的情况。设 p 是指向双向链表中的某一结点，即 p 存储的是该结点的地址，现要将一个结点 s 插入到结点 p 的后面。

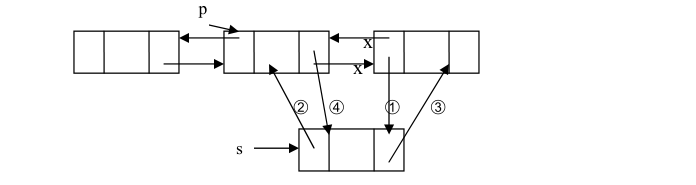
　　　　操作如下：

　　　　➀ p.Next.Prev = s;

　　　　➁ s.Prev = p;

　　　　➂ s.Next = p.Next;

　　　　➃ p.Next = s;

　　　　注：引用域值的操作的顺序不是唯一的，但也不是任意的，操作➂必须放到操作➃的前面完成，否则 p 直接后继结点的就找不到了。

　　3.4.3：双向链表删除：以在结点之后删除为例来说明在双向链表中删除结点的情况。设 p 是指向双向链表中的某一结点，即 p 存储的是该结点的地址，删除该节点P如下图所示

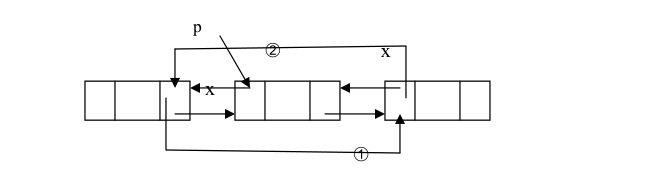
　　操作如下：

　　➀ p.Next = P.Next.Next;

　　➁ p.Next.Prev = p.Prev;

　　3.5：循环链表　　

　　　　有些应用不需要链表中有明显的头尾结点。在这种情况下，可能需要方便地从最后一个结点访问到第一个结点。此时，最后一个结点的引用域不是空引用，而是保存的第一个结点的地址（如果该链表带结点，则保存的是头结点的地址），也就是头引用的值。带头结点的循环链表( Circular Linked List )　　

　　

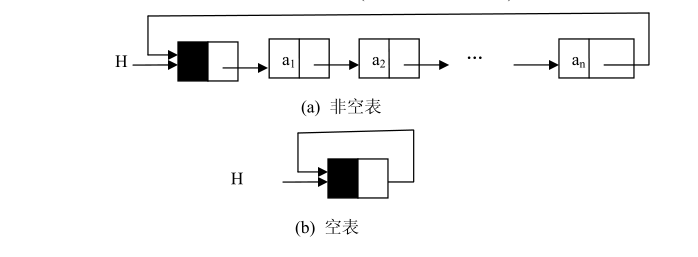
　　　　循环链表的基本操作与单链表大体相同，只是判断链表结束的条件并不是判断结点的引用域是否为空，而是判断结点的引用域是否为头引用，其它没有较大的变化。

四：c#中的线性表

　　4.1：C# 1.1 中只提供了非泛型 IList 接口，接口中项的类型是 object。非泛型 IList 接口是从 ICollection 接口继承而来，是所有线性表的基接口。

　　4.2：非泛型的 IList 接口的声明如下：

 interface IList : ICollection,IEnumerable
 {
 //公有属性
 bool IsFixedSize{get;} //只读，如果 IList 有固定大小，
 //其值为 true,否则为 false。
 bool IsReadOnly{get;} //只读，如果 IList 是只读的，
 //其值为 true,否则为 false。
 object this [T index] {get;set;} //索引器，得到或设置某个索引的项
 //公有方法
 int Add(object value); //添加某项到表中,返回被插入的新项
 //在表中的位置。
 void Clear(); //清空表。
 int IndexOf(object value); //如果表中有与 value 相等的项，
 //返回其在表中的索引,否则，返回-1。
 bool Contains(object value); //如果表中有与 value 相等的项，
 //返回 true，否则为 false。
 void Insert(int index,object value); //把值为 value 的项插入到索
 //引为 index 的位置。
 void Remove(object value); //删除表中第一个值为 value 的项。
 void RemoveAt(int index); //删除表中索引 index 处的项。
 }

　　4.3：NET 框架中的一些集合类实现了 IList 接口，如 ArrayList、ListDictionary、StringCollection、StringDictionary。下面以 ArrayList 为例进行说明，其它类的具体情况读者可参看.NET 框架的有关书籍。ArrayList 类使用数组来实现 IList 接口，所以 ArrayList 可看作顺序表。ArrayList 的容量可动态增长，通常情况下，当 ArrayList 中的元素满时，容量增加一倍，把原来的元素复制到新的空间中。当在 ArrayList 中插入一个元素时，该元素被添加到 ArrayList 的尾部，元素个数自动加 1。另外，需要注意的是，ArrayList 中对元素的操作前提是 ArrayList 是一个有序表，但 ArrayList 本身并不一定是有序的。所以，在对 ArrayList 中的元素进行操作之前，应该对 ArrayList进行排序。

　　4.4：在 C# 2.0 中不仅提供了非泛型的 Ilist 接口，而且还提供了泛型 Ilist 接口。泛型 Ilist 接口是从 Icollection 泛型接口继承而来，是所有的泛型表的基接口。实现泛型 Ilist 接口的集合提供类似于列表的语法，包括在列表中任意点访问个别项以及插入和删除成员等操作。

　　4.5：型的 Ilist 接口的声明如下：

 public inrterface Ilist<T> : Icollection<T>,Ienumerable<T>,
 Ienumerable
 {
 //公有属性
 T this [int index] {get;set;} //索引器，得到或设置某个索引的项
 //公有方法
 int IndexOf(T value); //如果表中有与 value 相等的项，返回
 //其在表中的索引,否则，返回-1。
 Void Insert(int index,T value); //把值为 value 的项插入到索
 //引为 index 的位置。
 Void Remove(T value); //删除表中第一个值为 value 的项。
 }

　　4.6：List<T>优点

　　List<T>是 ArrayList 在泛型中的替代品。List<T>的性能比 ArrayList 有很大改变，因为动态数组是.NET 程序使用的最基本的数据结构之一，它的性能影响到应用程序的全局。例如，以前 ArrayList 默认的 Capacity 是 16，而 List<T>的默认 Capacity 是 4，这样可以尽量减小应用程序的工作集。另外，List<T>的方法不是虚拟方法（ArrayList 的方法是虚拟方法），这样可以利用函数内联来提高性能（虚函数不可以被内联）。List<T>也不支持问题很多的 Synchronized 同步访问模式。

五：总结

　　线性表是最简单、最基本、最常用的数据结构，线性表的特点是数据元素之间存在一对一的线性关系，也就是说，除第一个和最后一个数据元素外，其余数据元素都有且只有一个直接前驱和直接后继。

　　线性表有两种不同的存储结构，即顺序存储结构和链式存储结构。顺序存储的线性表称为顺序表，顺序表中的存储单元是连续的，在 C#语言中用数组来实现顺序存储。链式存储的线性表称为链表，链表中的存储单元不一定是连续的，所以在一个结点有数据域存放数据元素本身的信息，还有引用域存放其相邻的数据元素的地址信息。单链表的结点只有一个引用域，存放其直接后继结点的地址信息，双向链表的结点有两个引用域，存放其直接前驱结点和直接后继结点的地址信息。循环链表的最后一个结点的引用域存放头引用的值。

　　对线性表的基本操作有查找、插入、删除等操作。顺序表由于具有随机存储的特点，所以查找比较方便，效率很高，但插入和删除数据元素都需要移动大量的数据元素，所以效率很低。而链表由于其存储空间不要求是连续的，所以插入和删除数据元素的效率很高，但查找需要从头引用开始遍历链表，所以效率很低。因此，线性表采用何种存储结构取决于实际问题，如果只是进行查找等操作而不经常插入和删除线性表中的数据元素，则线性表采用顺序存储结构；反之，采用链式存储结构。