字典学习（Dictionary Learning, KSVD）详解

注：字典学习也是一种数据降维的方法，这里我用到SVD的知识，对SVD不太理解的地方，可以看看这篇博客：《SVD（奇异值分解）小结 》；数据集：https://pan.baidu.com/s/1ZmpUSIscy4VltcimwwIWew

1、字典学习思想

字典学习的思想应该源来实际生活中的字典的概念。字典是前辈们学习总结的精华，当我们需要学习新的知识的时候，不必与先辈们一样去学习先辈们所有学习过的知识，我们可以参考先辈们给我们总结的字典，通过查阅这些字典，我们可以大致学会到这些知识。

为了将上述过程用准确的数学语言描述出来，我们需要将“总结字典”、“查阅字典”做出一个更为准确的描述。就从我们的常识出发：

1. 我们通常会要求的我们的字典尽可能全面，也就是说总结出的字典不能漏下关键的知识点。
2. 查字典的时候，我们想要我们查字典的过程尽可能简洁，迅速，准确。即，查字典要快、准、狠。
3. 查到的结果，要尽可能地还原出原来知识。当然，如果要完全还原出来，那么这个字典和查字典的方法会变得非常复杂，所以我们只需要尽可能地还原出原知识点即可。

注： 以上内容，完全是自己的理解，如有不当之处，欢迎各位拍砖。

下面，我们要讨论的就是如何将上述问题抽象成一个数学问题，并解决这个问题。

2、字典学习数学模型

2.1 数学描述

我们将上面的所提到的关键点用几个数学符号表示一下：

• “以前的知识”，更专业一点，我们称之为原始样本，用矩阵\(\mathbf{Y}\)表示；
• “字典”，我们称之为字典矩阵，用\(\mathbf{D}\)表示，“字典”中的词条，我们称之为原子（atom），用列向量\(\mathbf{d}_k\)表示；
• “查字典的方法”，我们称为稀疏矩阵，用\(\mathbf{X}\)；
• “查字典的过程”，我们可以用矩阵的乘法来表示，即\(\mathbf{DX}\)。

用数学语言描述，字典学习的主要思想是，利用包含\(K\)个原子\(\mathbf{d}_k\)的字典矩阵\(\mathbf{D}\in \mathbf{R}^{m \times K}\)，稀疏线性表示原始样本\(\mathbf{Y} \in \mathbf{R}^{m \times n}\)（其中\(m\)表示样本数，\(n\)表示样本的属性），即有\(\mathbf{Y=DX}\)（这只是我们理想的情况），其中\(\mathbf{X} \in \mathbf{R}^{K \times n}\)为稀疏矩阵，可以将上述问题用数学语言描述为如下优化问题

\[\min_{\mathbf{D,\ X}}{\|\mathbf{Y}-\mathbf{DX}\|^2_F},\quad \text{s.t.}\ \forall i,\ \|\mathbf{x}_i\|_0 \le T_0
\tag{2-1}
\]

或者

\[\min_{\mathbf{D,\ X}}\sum_i\|\mathbf{x}_i\|_0,
\quad \text{s.t.}\ \min_{\mathbf{D,\ X}}{\|\mathbf{Y}-\mathbf{DX}\|^2_F} \le \epsilon,
\tag{2-2}
\]

上式中\(\mathbf{X}\)为稀疏编码的矩阵，\(\mathbf{x}_i\,\ (i=1,2,\cdots,K)\)为该矩阵中的行向量，代表字典矩阵的系数。

注： \(\|\mathbf{x}_i\|_0\)表示零阶范数，它表示向量中不为0的数的个数。

2.2 求解问题

式（2-1）的目标函数表示，我们要最小化查完的字典与原始样本的误差，即要尽可能还原出原始样本；它的限的制条件\(\|\mathbf{x}_i\|_0 \le T_0\)，表示查字典的方式要尽可能简单，即\(\mathbf{X}\)要尽可能稀疏。式（2-2）同理。

式（2-1）或式（2-2）是一个带有约束的优化问题，可以利用拉格朗日乘子法将其转化为无约束优化问题

\[\min_{\mathbf{D,\ X}}{\|\mathbf{Y}-\mathbf{DX}\|^2_F}+\lambda\|\mathbf{x}_i\|_1
\tag{2-3}
\]

注： 我们将\(\|\mathbf{x}_i\|_0\)用\(\|\mathbf{x}_i\|_1\)代替，主要是\(\|\mathbf{x}_i\|_1\)更加便于求解。

这里有两个优化变量\(\mathbf{D,\ X}\)，为解决这个优化问题，一般是固定其中一个优化变量，优化另一个变量，如此交替进行。式（2-3）中的稀疏矩阵\(\mathbf{X}\)可以利用已有经典算法求解，如Lasso（Least Absolute Shrinkage and Selection Operator）、OMP（Orthogonal Matching Pursuit），这里我重点讲述如何更新字典\(\mathbf{D}\)，对更新\(\mathbf{X}\)不多做讨论。

假设\(\mathbf{X}\)是已知的，我们逐列更新字典。下面我们仅更新字典的第\(k\)列，记\(\mathbf{d}_k\)为字典\(\mathbf{D}\)的第\(k\)列向量，记\(\mathbf{x}^k_T\)为稀疏矩阵\(\mathbf{X}\)的第\(k\)行向量，那么对式（2-1），我们有

\[\begin{aligned}
{\|\mathbf{Y}-\mathbf{DX}\|^2_F}
=&\left\|\mathbf{Y}-\sum^K_{j=1}\mathbf{d}_j\mathbf{x}^j_T\right\|^2_F \\
=&\left\|\left(\mathbf{Y}-\sum_{j\ne k}\mathbf{d}_j\mathbf{x}^j_T\right)-\mathbf{d}_k\mathbf{x}^k_T\right\|^2_F\\
=&\left\|\mathbf{E}_k - \mathbf{d}_k\mathbf{x}_T^k \right\|^2_F
\end{aligned}
\tag{2-4}
\]

上式中残差\(\mathbf{E}_k=\mathbf{Y}-\sum_{j\ne k}\mathbf{d}_j\mathbf{x}^j_T\)，

此时优化问题可描述为

\[\min_{\mathbf{d}_k,\ \mathbf{x}^k_T}\left\|\mathbf{E}_k - \mathbf{d}_k\mathbf{x}_T^k \right\|^2_F
\]

因此我们需要求出最优的\(\mathbf{d}_k,\ \mathbf{x}_T^k\)，这是一个最小二乘问题，可以利用最小二乘的方法求解，或者可以利用SVD进行求解，这里利用SVD的方式求解出两个优化变量。

但是，在这里我人需要注意的是，不能直接利用\(\mathbf{E}_k\)进行求解，否则求得的新的\(\mathbf{x}_k^T\)不稀疏。因此我们需要将\(\mathbf{E}_k\)中对应的\(\mathbf{x}_T^k\)不为0的位置提取出来，得到新的\(\mathbf{E}_k^{'}\)，这个过程如图2-1所示，这样描述更加清晰。

图2-1 提取部分残差

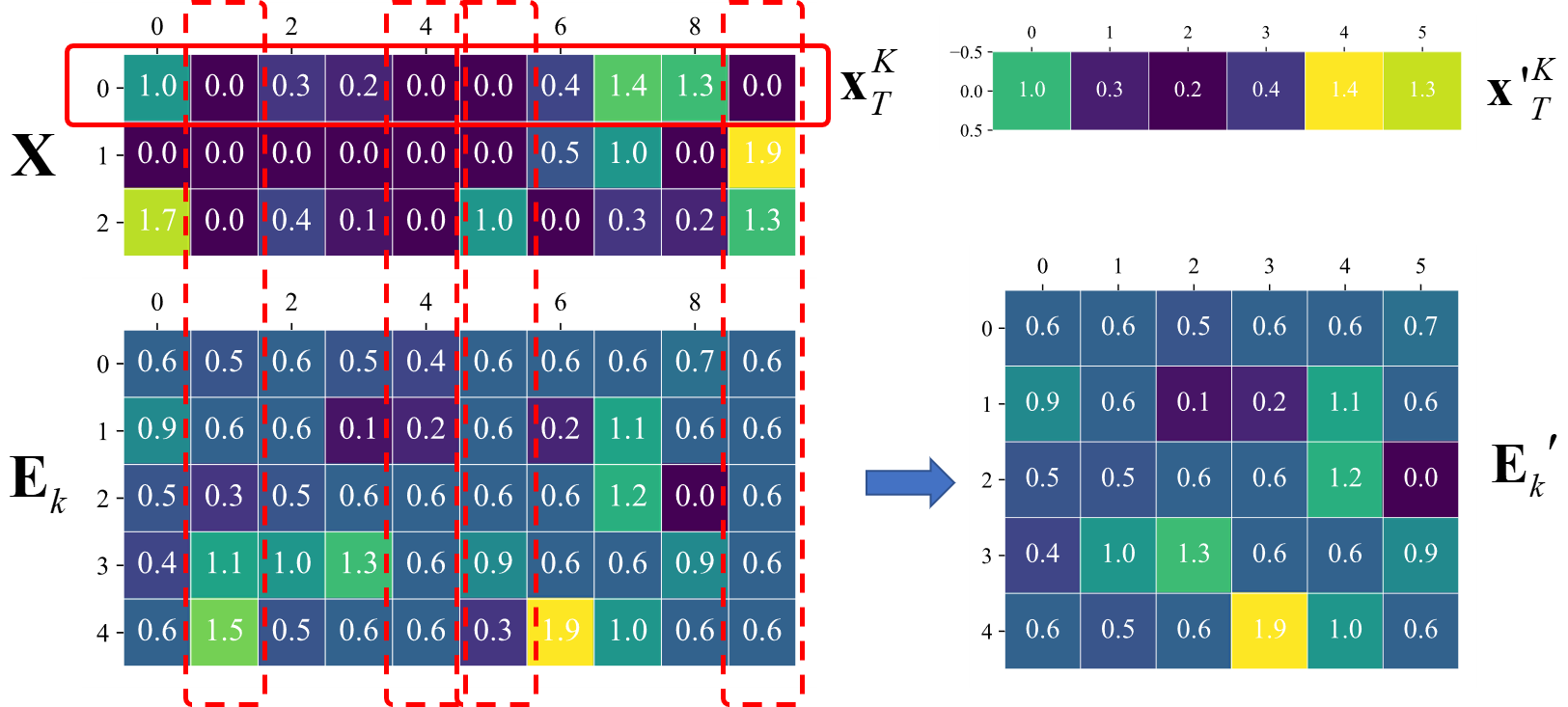
如上图，假设我们要更新第0列原子，我们将\(\mathbf{x}_T^k\)中为零的位置找出来，然后把\(\mathbf{E}_k\)对应的位置删除，得到\(\mathbf{E}_k^{'}\)，此时优化问题可描述为

\[\min_{\mathbf{d}_k,\ \mathbf{x}^k_T}\left\|\mathbf{E}_k^{'} - \mathbf{d}_k\mathbf{x{'}}_T^{k} \right\|^2_F
\tag{2-5}
\]

因此我们需要求出最优的\(\mathbf{d}_k,\ \mathbf{x^{'}}_T^k\)

\[\mathbf{E}_k^{'}=U\Sigma V^T
\tag{2-6}
\]

取左奇异矩阵\(U\)的第1个列向量\(\mathbf{u}_1=U(\cdot,1)\)作为\(\mathbf{d}_k\)，即\(\mathbf{d}_k=\mathbf{u}_1\)，取右奇异矩阵的第1个行向量与第1个奇异值的乘积作为\(\mathbf{x{'}}_T^k\)，即\(\mathbf{x{'}}^k_T=\Sigma(1,1)V^T(1,\cdot)\)。得到\(\mathbf{x{'}}^k_T\)后，将其对应地更新到原\(\mathbf{x}_T^k\)。

注： 式（2-6）所求得的奇异值矩阵\(\Sigma\)中的奇异值应从大到小排列；同样也有\(\mathbf{x{'}}^k_T=\Sigma(1,1)V(\cdot,1)^T\)，这与上面\(\mathbf{x{'}}^k_T\)的求法是相等的。

2.3 字典学习算法实现

据2.2小节，利用稀疏算法求解得到稀疏矩阵\(\mathbf{X}\)后，逐列更新字典，有如下算法1.1。

算法1.1：字典学习（K-SVD）

输入：原始样本，字典，稀疏矩阵

输出：字典，稀疏矩阵

1. 初始化： 从原始样本\(Y \in \mathbf{R}^{m \times n}\)随机取\(K\)个列向量或者取它的左奇异矩阵的前\(K\)个列向量\(\{\mathbf{d}_1,\mathbf{d}_2,\cdots,\mathbf{d}_K\}\)作为初始字典的原子，得到字典\(\mathbf{D}^{(0)} \in \mathbf{R}^{m \times K}\)。令\(j=0\)，重复下面步骤2-3，直到达到指定的迭代步数，或收敛到指定的误差：

2. 稀疏编码： 利用字典上一步得到的字典\(\mathbf{D}^{(j)}\)，稀疏编码，得到\(\mathbf{X}^{(j)}\in\mathbf{R}^{K \times n}\)。

3. 字典更新： 逐列更新字典\(\mathbf{D}^{(j)}\)，字典的列\(\mathbf{d}_k \in \{\mathbf{d}_1,\mathbf{d}_2,\cdots,\mathbf{d}_K\}\)

   • 当更新\(\mathbf{d}_k\)时，计算误差矩阵\(\mathbf{E}_k\)

     \[\mathbf{E}_k=\mathbf{Y}-\sum_{j\ne k}\mathbf{d}_j\mathbf{x}^j_T.
     \]

   • 取出稀疏矩阵第\(k\)个行向量\(\mathbf{x}^k_T\)不为0的索引的集合\(\omega_k = \{i|1\le i\le n,\ \mathbf{x}_T^k(i) \ne 0\}\)，\(\mathbf{x'}_T^{k} = \{\mathbf{x}_T^k(i)|1\le i\le n,\ \mathbf{x}_T^k(i) \ne 0\}\)

   • 从\(\mathbf{E}_k\)取出对应\(\omega_k\)不为0的列，得到\(\mathbf{E}_k^{'}\).

   • 对\(\mathbf{E}_k^{'}\)作奇异值分解\(\mathbf{E}_k=U\Sigma V^T\)，取\(U\)的第1列更新字典的第\(k\)列，即\(\mathbf{d}_k=U(\cdot,1)\)；令\(\mathbf{x'}^k_T=\Sigma(1,1)V(\cdot,1)^T\)，得到\(\mathbf{x{'}}^k_T\)后，将其对应地更新到原\(\mathbf{x}_T^k\)。

   • \(j = j + 1\)

3、字典学习Python实现

以下实验的运行环境为python3.6+jupyter5.4。

载入数据

import numpy as np
import pandas as pd
from scipy.io import loadmat

train_data_mat = loadmat("../data/train_data2.mat")

train_data = train_data_mat["Data"]
train_label = train_data_mat["Label"]

print(train_data.shape, train_label.shape)

注： 上面的数据集，可以随便使用一个，也可以随便找一个张图片。

初始化字典

u, s, v = np.linalg.svd(train_data)
n_comp = 50
dict_data = u[:, :n_comp]

字典更新

def dict_update(y, d, x, n_components):
    """
    使用KSVD更新字典的过程
    """
    for i in range(n_components):
        index = np.nonzero(x[i, :])[0]
        if len(index) == 0:
            continue
        # 更新第i列
        d[:, i] = 0
        # 计算误差矩阵
        r = (y - np.dot(d, x))[:, index]
        # 利用svd的方法，来求解更新字典和稀疏系数矩阵
        u, s, v = np.linalg.svd(r, full_matrices=False)
        # 使用左奇异矩阵的第0列更新字典
        d[:, i] = u[:, 0]
        # 使用第0个奇异值和右奇异矩阵的第0行的乘积更新稀疏系数矩阵
        for j,k in enumerate(index):
            x[i, k] = s[0] * v[0, j]
    return d, x

注： 上面代码的16~17需要注意python的numpy中的普通索引和花式索引的区别，花式索引会产生一个原数组的副本，所以对花式索引的操作并不会改变原数据，因此不能像第10行一样，需利用直接索引更新x。

迭代更新求解

可以指定迭代更新的次数，或者指定收敛的误差。

from sklearn import linear_model

max_iter = 10
dictionary = dict_data

y = train_data
tolerance = 1e-6

for i in range(max_iter):
    # 稀疏编码
    x = linear_model.orthogonal_mp(dictionary, y)
    e = np.linalg.norm(y - np.dot(dictionary, x))
    if e < tolerance:
        break
    dict_update(y, dictionary, x, n_comp)

sparsecode = linear_model.orthogonal_mp(dictionary, y)

train_restruct = dictionary.dot(sparsecode)