洛谷 P2672 推销员

题目传送门

解题思路:

我们会发现本题有一个特性,就是如果我们走到一个更远的地方,那么近的地方距离原点的距离我们可以忽略.

本题要求最大的疲劳值,所以我们需要排序,第一个想到堆,反正我是先想到堆.

然后我们再看题目,因为最后疲劳值是由两部分组成的:路径疲劳值和推销疲劳值.又因为第一行提到的,所以我们可以选一个点k(后面解释),将每个状态下分为两种点:

1.比当前k点距离原点更近,这些点的疲劳值其实只有推销疲劳值,因为我们已经走得更远了,所以顺道处理这些就行,不需要走多余的路

2.比当前k点距离原点更远,这些点的疲劳值其实就是推销疲劳值+两倍路径疲劳值-两倍k的路径疲劳值

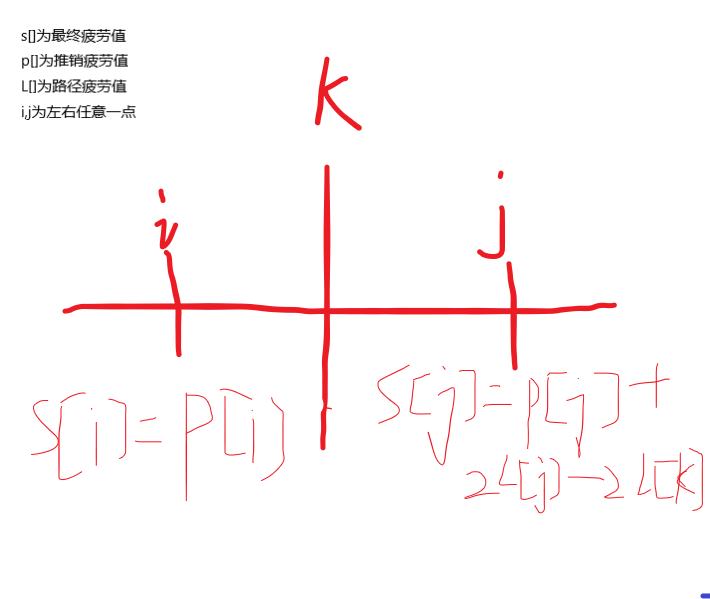
而其实最大疲劳值就是这两种点各自的最大值的最大值,所以我们可以用两个大根堆来存,取两个堆顶的较大值即可.

返回来,k是什么呢?k就是我们当前已经选过的点里最靠右的.

为什么呢?因为对我们来说只要某个点走了,则这个点左边所有点我们都可以顺路经过,并不需要多余路径疲劳值,所以我们只要记录最右即可.

代码处理的一些细节:

1.一开始右边的堆将所有点放进去,左边堆为空,选一个最大点为第一个k.

2.每当我更新一个k,我再将k左边所有的点推进左边堆.不这么做也可,只是这样代码好写

3.那么我们更新k后怎么判断右边堆那些在当前k的左边呢?因为k是动态的,所以原来在右边的可能到右边我们只要判断当前元素和k谁到原点近即可,所以我们要不单要记录疲劳值,还要记录路径值,所以我们要定义结构体来构造堆.

AC代码:

 #include<cstdio>
 #include<iostream>
 #include<queue>
 #include<algorithm>

 using namespace std;

 struct node {
     int v, distance,ans;//推销值,距离值,最终值
     node() { }
     bool operator < (const node & p) const {
         return v +  * distance < p.v +  * p.distance;//按照疲劳值由大到小排序
     }
 }e[];

 struct kkk {
     int _v,_distance;
 }_e[];

 priority_queue <node> b;//右边堆
 priority_queue <int> a;//左边堆
 int n,A,vv[],k,bj,m,n1;

 bool cmp(kkk aa,kkk bb) {
     return aa._distance < bb._distance;
 }

 void solve() {//解题过程
     while(n1--) {
         if(b.top().ans -  * k >= a.top()) {//我忍不住要吐槽,将ans改成v,能得一半分,另一半TLE,这数据太弱了,害得我以为自己代码时间复杂度太高
             if(b.top().distance <= k) {
                 b.pop();
                 n1++;
                 continue;
             }
             m += b.top().ans -  * k;
             k = b.top().distance;
             b.pop();
             for(;bj <= n; bj++)
                 if(_e[bj]._distance >= k)
                     break;
                 else
                     a.push(_e[bj]._v);
         }
         else {
             m += a.top();
             a.pop();
         }
         printf("%d\n",m);
     }
 }

 void firstime() {//第一次处理,之后便与解题思路一致
     m = b.top().ans;
     cout << m << endl;
     n1 = n;
     n1--;
     k = b.top().distance;
     b.pop();
     for(bj = ;bj <= n; bj++)
         if(_e[bj]._distance >= k)
             break;
         else
             a.push(_e[bj]._v);
 } 

 int main()
 {
     scanf("%d",&n);
     for(int i = ;i <= n; i++) {
         scanf("%d",&e[i].distance);
         _e[i]._distance = e[i].distance;
     }
     for(int i = ;i <= n; i++) {
         scanf("%d",&vv[i]);
         _e[i]._v = e[i].v = vv[i];
         e[i].ans = e[i].v +  * e[i].distance;
         b.push(e[i]);
     }
     sort(_e+,_e++n,cmp);//按照距离原点远近排序
     firstime();
     solve();
     return ;
 }

//NOIP普及 2015 T4