【ZJOI2017 Round2练习&BZOJ4827】D1T3 gift（FFT）

题意：

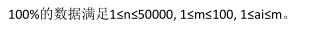
思路：可以看出题目所要最小化的是这样一个形式：

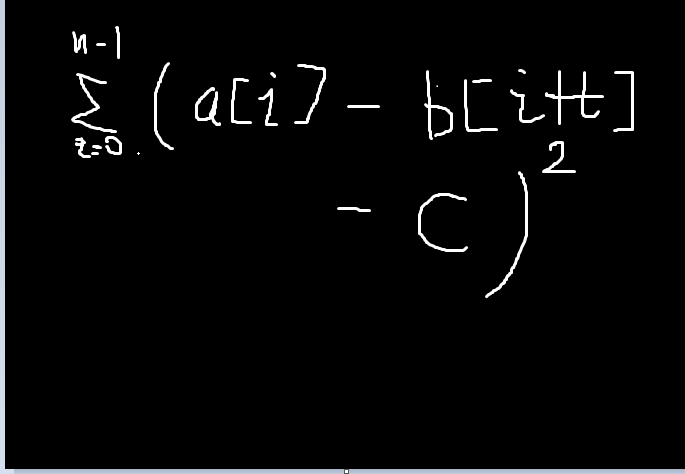
拆出每一项之后发现会变化的项只有sigma a[i]*b[i+t]与c^2,c*(a[i]-b[i])

c可以在外层枚举，剩下的只有sigma a[i]*b[i+t] (i=0..n-1)

因为FFT只能解决simga a[i]*b[n-i]

所以我们可以把a翻转，这样就化成了如上的形式

c[n+t+1]=a[n-i+1]*b[i+t] (i=0..n-1)

取出最小（大）的c[i]，与外层枚举的c共同求出答案，取最小值

FFT模板，值得一背

 type cp=record
          x,y:extended;
         end;
      arr=array[..]of cp;
 var c,d,cur:arr;
     a,b:array[..]of longint;
     n,i,m:longint;
     ans,sum,s1,s2:int64;

 procedure swap(var x,y:cp);
 var t:cp;
 begin
  t:=x; x:=y; y:=t;
 end;

 function jia(a,b:cp;f:longint):cp;
 begin
  if f=- then
  begin
   b.x:=-b.x; b.y:=-b.y;
  end;
  jia.x:=a.x+b.x;
  jia.y:=a.y+b.y;
 end;

 function mult(a,b:cp):cp;
 begin
  mult.x:=a.x*b.x-a.y*b.y;
  mult.y:=a.x*b.y+a.y*b.x;
 end;

 function min(x,y:int64):int64;
 begin
  if x<y then exit(x);
  exit(y);
 end;

 function max(x,y:int64):int64;
 begin
  if x>y then exit(x);
  exit(y);
 end;

 procedure fft(var a:arr;n,f:longint);
 var i,j,k,m:longint;
     w,u,v:cp;
 begin
  i:=n>>; j:=;
  while j<n do
  begin
   if i<j then swap(a[i],a[j]);
   k:=n>>;
   while k and i> do
   begin
    i:=i xor k;
    k:=k>>;
   end;
   i:=i xor k;
   inc(j);
  end;
  m:=;
  while m<=n do
  begin
   w.x:=cos(*pi*f/m); w.y:=sin(*pi*f/m);
   cur[].x:=; cur[].y:=;
   for i:= to m- do cur[i]:=mult(cur[i-],w);
   i:=;
   while i<n do
   begin
    j:=i;
    while j<i+(m>>) do
    begin
     u:=a[j]; v:=mult(a[j+(m>>)],cur[j-i]);
     a[j]:=jia(u,v,);
     a[j+(m>>)]:=jia(u,v,-);
     inc(j);
    end;
    i:=i+m;
   end;
   m:=m<<;
  end;
 end;

 procedure solve;
 var i,j,len:longint;
 begin
  for i:= to n- do c[i].x:=a[i];
  for i:= to n- do d[i].x:=b[i];
  i:=; j:=n-;
  while i<=j do
  begin
   swap(d[i],d[j]);
   inc(i); dec(j);
  end;
  len:=;
  while len<=n+n do len:=len<<;
  for i:=n to len- do
  begin
   c[i].x:=; d[i].x:=;
  end;
  for i:= to len- do
  begin
   c[i].y:=; d[i].y:=;
  end;
  fft(c,len,);
  fft(d,len,);
  for i:= to len- do c[i]:=mult(c[i],d[i]);
  fft(c,len,-);
  for i:= to len- do c[i].x:=trunc(c[i].x/len+0.5);
  for i:=n to len- do c[i mod n].x:=c[i mod n].x+c[i].x;
  sum:=-(<<);
  for i:= to n- do sum:=max(sum,round(c[i].x));
  sum:=-sum*;
 end;

 begin
  assign(input,'bzoj4827.in'); reset(input);
  assign(output,'bzoj4827.out'); rewrite(output);
  readln(n,m);
  for i:= to n- do read(a[i]);
  for i:= to n- do read(b[i]);
  ans:=<<;
  solve;
  for i:= to n- do
  begin
   s1:=s1+a[i]-b[i];
   s2:=s2+a[i]*a[i]+b[i]*b[i];
  end;
  for i:=-m to m do ans:=min(ans,int64(n)*i*i+*s1*i+s2+sum);
  writeln(ans);
  close(input);
  close(output);
 end.