HDU1054 Strategic Game —— 最小点覆盖 or 树形DP

题目链接：https://vjudge.net/problem/HDU-1054

Strategic Game

Time Limit: 20000/10000 MS (Java/Others)    Memory Limit: 65536/32768 K (Java/Others)
Total Submission(s): 8673    Accepted Submission(s): 4174

Problem Description

Bob enjoys playing computer games, especially strategic games, but sometimes he cannot find the solution fast enough and then he is very sad. Now he has the following problem. He must defend a medieval city, the roads of which form a tree. He has to put the minimum number of soldiers on the nodes so that they can observe all the edges. Can you help him?

Your program should find the minimum number of soldiers that Bob has to put for a given tree.

The input file contains several data sets in text format. Each data set represents a tree with the following description:

the number of nodes
the description of each node in the following format
node_identifier:(number_of_roads) node_identifier1 node_identifier2 ... node_identifier
or
node_identifier:(0)

The node identifiers are integer numbers between 0 and n-1, for n nodes (0 < n <= 1500). Every edge appears only once in the input data.

For example for the tree:

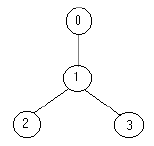
the solution is one soldier ( at the node 1).

The output should be printed on the standard output. For each given input data set, print one integer number in a single line that gives the result (the minimum number of soldiers). An example is given in the following table:

 

Sample Input

4
0:(1) 1
1:(2) 2 3
2:(0)
3:(0)
5
3:(3) 1 4 2
1:(1) 0
2:(0)
0:(0)
4:(0)

 

Sample Output

1
2

 

Source

Southeastern Europe 2000

最小点覆盖：

 #include<cstdio>
 #include<cstring>
 #include<vector>
 using namespace std;

 vector<int>G[];
 bool vis[];
 int match[];

 bool dfs(int u)
 {
     for(int i = ; i<G[u].size(); i++)
     {
         int t = G[u][i];
         if(!vis[t])
         {
             vis[t] = true;
             if(match[t]==- || dfs(match[t]))
             {
                 match[t] = u;
                 return true;
             }
         }
     }
     return false;
 }

 int main()
 {
     int n,m,k,a,ans;
     while(scanf("%d",&n)==)
     {
         for(int i = ; i<n; i++)
             G[i].clear();
         for(int i = ; i<n; i++)
         {
             scanf("%d:(%d)",&m,&k);
             for(int j = ; j<k; j++)
             {
                 scanf("%d",&a);
                 G[m].push_back(a);
                 G[a].push_back(m);
             }
         }

         ans = ;
         memset(match,-,sizeof(match));
         for(int i = ; i<n; i++)
         {
             memset(vis,false,sizeof(vis));
             if(dfs(i))
                 ans++;
         }

         printf("%d\n",ans/);
     }
 }

树形DP：

 #include<cstdio>
 #include<cstring>
 #include<algorithm>
 using namespace std;

 struct
 {
     int to, next;
 }e[];

 int h[], dp[][], num;

 void addedge(int u, int v)
 {
     e[num].to = v;
     e[num].next = h[u];
     h[u] = num++;
 }

 int dfs(int u)
 {
     int v;
     dp[u][] = ; dp[u][] = ;
     for(int i = h[u]; i!=-; i = e[i].next)
     {
         v = e[i].to;
         dfs(v);
         dp[u][] += dp[v][];
         dp[u][] += min(dp[v][],dp[v][]);
     }
     return min(dp[u][], dp[u][]);
 }

 int main()
 {
     int n,m,u,v,k,rt;
     while(~scanf("%d",&n))
     {
         memset(h,-,sizeof(h));
         rt = -; num = ;
         for(int i = ; i<n; i++)
         {
             scanf("%d:(%d)",&u,&k);
             for(int j = ; j<k; j++)
             {
                 scanf("%d",&v);
                 addedge(u,v);
             }

             if(rt==-) rt = u;
         }

         printf("%d\n",dfs(rt));
     }
 }