cf468C Hack it!

Little X has met the following problem recently.

Let's define f(x) as the sum of digits in decimal representation of number x (for example, f(1234) = 1 + 2 + 3 + 4). You are to calculate

Of course Little X has solved this problem quickly, has locked it, and then has tried to hack others. He has seen the following C++ code:

    ans = solve(l, r) % a;
    if (ans <= 0)
      ans += a;

This code will fail only on the test with 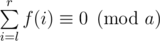. You are given number a, help Little X to find a proper test for hack.

Input

The first line contains a single integer a (1 ≤ a ≤ 10¹⁸).

Output

Print two integers: l, r (1 ≤ l ≤ r < 10²⁰⁰) — the required test data. Leading zeros aren't allowed. It's guaranteed that the solution exists.

Examples

Input

46

Output

1 10

Input

126444381000032

Output

2333333 2333333333333

这题贼鸡儿恶心

令f(x)表示x各个位上数字之和，给个p，要求构造一组[l,r]，使得{f(l)+f(l+1)+...+f(r)} % p = 0

注意到p<=10^18,当x<=10^18时，又有这样的式子成立：f(10^18+x)=f(x)+1   （这很显然，因为就在最前面加了个1）

所以，如果[l,r]表示{f(l)+f(l+1)+...+f(r)} % p

假设[0,10^18] -> a

[1,10^18+1]->a+1

...

[p-a,10^18+p-a]->p (其实这里模p应该是0了)

这个区间就可以了

然后a不会算……就算了个[0,10^18-1]=8.1*10^19，所以右区间还要减一

这个数字好像还是爆long long的，需要81拆成9*9来搞

 #include<cstdio>
 int main()
 {
     long long p,t,e=1e18;scanf("%lld",&p);
     t=*e%p*%p;
     printf("%lld %lld\n",p-t,e-+p-t);
 }

cf 468C