KMP算法介绍

简介

KMP算法是D.E.Knuth、J.H.Morris和V.R.Pratt共同提出的，称之为Knuth-Morris-Pratt算法，简称KMP算法。该算法与Brute-Force算法相比有较大改进，主要是消除了主串指针的回溯，从而使算法效率有了某种程度的提高。

实现

1、从模式串t中提取加速匹配的信息

kmp就是通过模式串本身的特点来加速的，具体来说就是求next数组，next数组的定义如下：

$$next[j]=\begin{cases} -1 & 当j=0时\\MAX\{k \,|\, 0<k<j {\ } and {\ } "t_0t_1\cdot \cdot \cdot t_{k-1}"="t_{j-k}t_{j-k+1}\cdot \cdot \cdot t_{j-1}"\}&前后缀相等时\\0 &其它情况\end{cases}$$

next数组的求解过程如下：

next[0]=-1（特殊值，标记），next[1]=0（j=1，在1~j-1的位置上没有字符，属于其它情况）
如果next[j] = k，表示有$"t_0t_1\cdot \cdot \cdot t_{k-1}"="t_{j-k}t_{j-k+1}\cdot \cdot \cdot t_{j-1}"$：

若$t_k=t_j$，即有$"t_0t_1\cdot \cdot \cdot t_{k-1}t_k"="t_{j-k}t_{j-k+1}\cdot \cdot \cdot t_{j-1} t_j"$，显然有$next[j+1]=k+1$。
若$t_k\neq t_j$，说明$t_j$之前不存在长度为$next[j]+1$的字串和开头字符起的字串相同，那么是否存在一个长度较短的字串和开头字符起的字串相同呢？设${k}'=next[k]$（回退），则下一步应该将$t_j$与$t_{{k}'}$比较：若$t_j=t_{{k}'}$，则说明$t_j$之前存在长度为$next[{k}']+1$的字串和开头字符起的字串相同；否则依此类推找更短的字串。知道不存在可匹配的字串，置$next[j+1]=0$。所以，当$t_k \neq t_j时，置$k=next[k]$

例如：

求模式串$t="aaaba"$的next数组。

解：

j	0	1	2	3	4
t[j]	a	a	a	b	a
next[j]	-1	0	1	2	0

 //char x[]是模式串

 void pre_kmp()

 {

     int m = strlen(x);

     int i = , j = nexts[] = -;

     while (i < m)

     {

         while (j != - && x[i] != x[j])  j = nexts[j];    //当前不匹配，j回退，寻找是否存在一个长度较小的字串和开头的字串相等

         nexts[++i] = ++j;                //j等于已匹配的长度，如果当前位置也匹配，则nexts直接为j+1

     }

 }

2、KMP算法的模式匹配过程

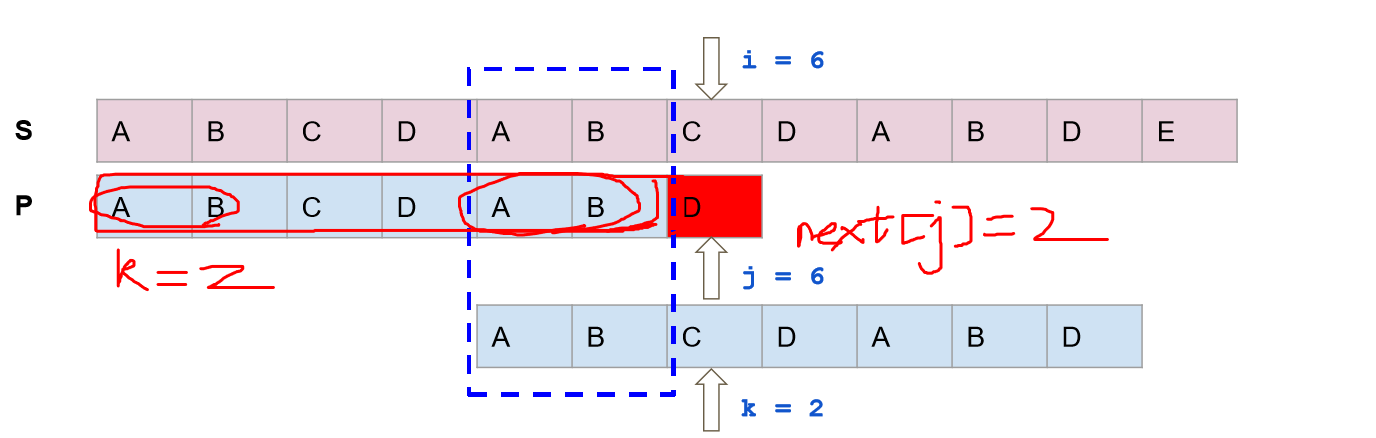
简单的说就是，若当前位置匹配则模式串和主串指针同时后移一位，若当前位置不匹配，则主串指针不动，模式串指针回退到next[i]，如果回退的位置上仍不匹配继续回退。

大概这样：

 //返回x在y中出现的次数（可重叠）

 int KMP_Count()    //x为模式串，y为主串

 {

     int i = , j = , ans = ;

     int m = strlen(x), n = strlen(y);

     pre_kmp();

     while (i < n)

     {

         while (j != - && y[i] != x[j])  j = nexts[j];        //当前位置不同，j回退

         i++; j++;                //当前位置相同，i、j同时后移一位

         if (j >= m)

         {

             ans++;

             j = nexts[j];

         }

     }

     return ans;

 }

注：

匹配时分为主串可重复和主串不可重复，两者只是在找到匹配串时模式串的回溯位置不同
next数组保证了真前缀和真后缀尽可能长的匹配，这样才能保证匹配时不会出现遗漏，同时模式串也能右移的更多
pre_kmp求next数组时求了字符串最后一个字符的下一位，因为做题时经常需要这个值

复杂度

一般化结论：

- 一个周期内的比较次数：1 * (M - 1) + M

- 周期长度：M

- 周期个数：N/M

- 比较总次数： 周期个数 * 一个周期内额比较次数 = (2 - 1/M)*N < 2N

所以最坏情况下模式串中每个字符的平均比较次数小于2，所以比较部分的平均时间复杂度为O(N)。

求next数组的过程其实主串与主串比较（KMP是将主串与模式串匹配），所以时间复杂度为O(M)。

总的时间复杂度为O(M+N)。

参考链接：