FPGA基础入门篇(四) 边沿检测电路

FPGA基础入门篇(四)——边沿检测电路

一、边沿检测

边沿检测，就是检测输入信号，或者FPGA内部逻辑信号的跳变，即上升沿或者下降沿的检测。在检测到所需要的边沿后产生一个高电平的脉冲。这在FPGA电路设计中相当的广泛。

没有复位的情况下，正常的工作流程如下：

（1）D触发器经过时钟clk的触发，输出trigger信号，保存了t0时刻的信号。
（2）同时由trigger通过非门输出信号，保留了当前时刻t1的触发信号
（3）经过与门输出信号pos_edge，neg_edge

a) 只有t0时刻为高，且t1时候为低的时候，与门输出高，此时为下降沿。

b) 只有to时候为低，且t1时候为高的时候，与门输出高，此时为上升沿。

当然，在复位的时刻，DFF被复位，无法检测触发信号。

二、采用一个触发器的边沿检测电路设计：

1. verilog代码实现：

//one trigger
module edge_detect(
input clk_i, rst_n_i, data_i, //输入端口
output posedge_o,negedge_o		//输出端口
);

//one regester
reg tri_1;

always@(posedge clk_i or negedge rst_n_i)
begin
    if (! rst_n_i)			//置位
    begin
        tri_1 <= 1'b0;
    end
    else
    begin
        tri_1 <= data_i;	//触发器
    end
end

assign negedge_o = tri_1 & (~data_i); 		//下降沿检测
assign posedge_o = (~tri_1) & data_i;     	//上升沿检测
endmodule

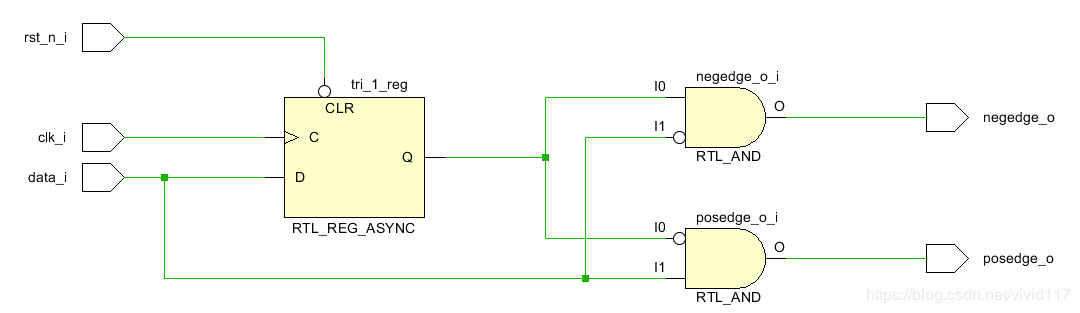
1. RTL电路
   
   用vivado RTL分析电路
   
   
2. 仿真代码及结果

module tb_test(
    );

reg clk_i,rst_n_i,data_i;
wire posedge_o, negedge_o;

//模块调用
edge_detect u1(
.clk_i(clk_i),
.rst_n_i(rst_n_i),
.data_i(data_i),
.posedge_o(posedge_o),
.negedge_o(negedge_o)
);

//initial
initial begin
clk_i = 0;
rst_n_i = 0;
#10
rst_n_i = 1;
data_i = 0;
#13
data_i = 1; 	//上升沿
#20
data_i = 0;		//下降沿
#15
data_i = 1;		//上升沿
#10
data_i = 0;		//下降沿
end

//clk 信号
always #5 clk_i = ~clk_i;

endmodule

仿真结果：



分析：在第一次上升沿时，由于上升沿离下个时钟上升沿间隔短，结果会产生“毛刺”

下面利用多个触发器可以延迟n-1个触发器的周期时间保证至少有一个时钟周期。

三、采用多个触发器的边沿检测电路设计：

1. verilog 语言实现(两个触发器及双边沿检测)

//two trigger
module edge_detect(
input clk_i, rst_n_i, data_i,
output posedge_o,negedge_o,double_edge_o
);

//two regester
reg tri_1;
reg tri_2;

always@(posedge clk_i or negedge rst_n_i)
begin
    if (! rst_n_i)			//置位
    begin
        tri_1 <= 1'b0;
        tri_2 <= 1'b0;
    end
    else
    begin
        tri_1 <= data_i;
        tri_2 <= tri_1;  	二级触发器
    end
end

assign negedge_o = tri_2 & (~tri_1);		//下降沿检测
assign posedge_o = (~tri_2) & tri_1;		//上升沿检测
assign double_edge_o = tri_1 ^ tri_2;		//双边沿检测

endmodule

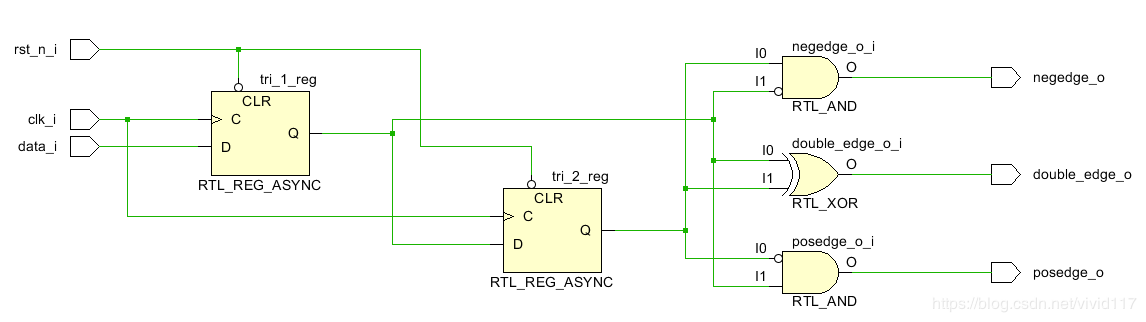
1. RTL电路
   
   用vivado RTL分析电路
   
   
2. 仿真结果：
   
   
   
   tri_1将输入与时钟同步，tri_2延迟一个时钟周期。级数越多，延迟越高。

可以看到边沿检测结果都出现在下一个时钟周期

四、边沿检测应用

边沿检测技术在项目应用中，非常低广泛。如要有效捕获信号跳变沿，边沿检测技术的应用是必不可少的。

有如下几个方面

（1）将时钟边沿使能转换为边沿检测使能，使时钟同步化。

（2）捕获信号的突变（UART，SPI等信号使能突变）

（3）逻辑分析仪中信号的边沿检测。

五、实现指标及存在缺陷

没有十全十美的东西，也没有十全十美的电路、代码；边沿检测技术亦如此。有如下缺陷：

（1）增大CLK信号可以增强边沿检测的效率，但不能滤去跳变的杂波。

（2）减少CLK可以有效滤去跳变的杂波，但不能及时检测到边沿跳变。

（3）增加DFF能更好的滤除杂波，寄存信号，但同时检测延时大。

参考博文: https://blog.csdn.net/u011412586/article/details/9971455

https://www.cnblogs.com/crazybingo/archive/2011/07/26/2117149.html