Luogu P3901 数列找不同

由于技术原因，题目我贴不上了，大家点下面的链接自己去看吧^_^

P3901 数列找不同

这题第一眼看去，题面真短，有坑（flag）

在往下面看去，woc数据这么大，你要怎样。

现在一起想想想，超级侦探，立刻出发。

bulabulabula，

串了。

看了看题解，卧槽，还有这种操作，赶紧get

我们在输入的时候做一下预处理，把每一个数前面的有和它重复的数的位置记录一下，然后在找的时候就很简单了。

不要以为这么简单就结束了。hahahha

代码

#include <iostream>
#include <cstdio>
#define MAXN 1000007

using namespace std;

int N, Q, a[MAXN], s, t;

int lef[MAXN];

int main() {
    scanf("%d%d", &N, &Q);
    for(int i=1; i<=N; i++) {
        scanf("%d", &a[i]);
        for(int j=1; j<i; j++) {
            if(a[i] == a[j]) {
                lef[i] = j;
            }
        }
    }
    for(int i=1; i<=Q; i++) {
        scanf("%d%d", &s, &t);
        bool mark = true;
        for(int j=s; j<=t; j++) {
            if(lef[j] >= s) {
                printf("No\n");
                mark = false;
                break;
            }
        }
        if(mark == true) {
            printf("Yes\n");
        }
    }
    return 0;
}

　　

　　

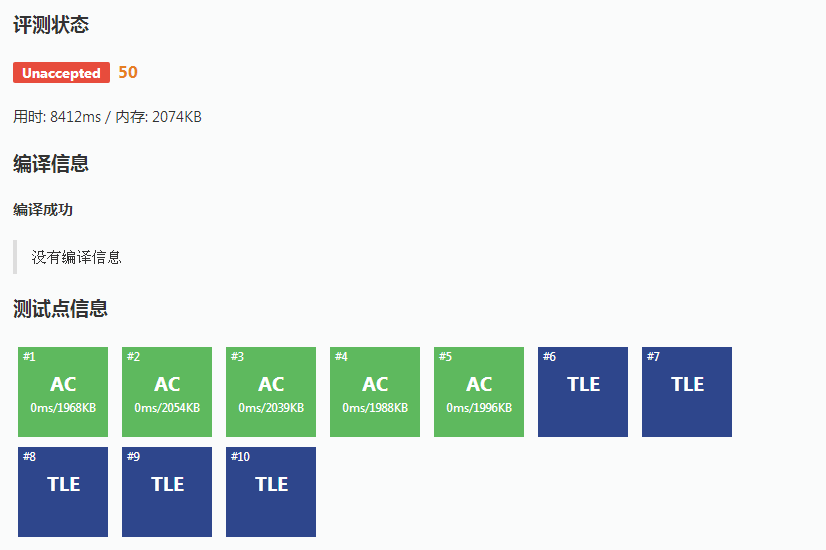
咦，我怎么才50分。原来死因为我的预处理是接近$O(n^2)$的，那还有什么好办法的吗？

别着急，接着写。

我们定义一个数组$la[j]$值为$j$的数最后的出现位置，这样就不用再循环去找了，就变成$O(n)$的复杂的了。

怎么还是TLE啊喂O—n—O

看看代码

#include <iostream>
#include <cstdio>
#define MAXN 1000007

using namespace std;

int N, Q, a[MAXN], s, t;

int lef[MAXN], la[MAXN];

int main() {
    scanf("%d%d", &N, &Q);
    for(int i=1; i<=N; i++) {
        scanf("%d", &a[i]);
        lef[i] = la[a[i]];
        la[a[i]] = i;
    }
    for(int i=1; i<=Q; i++) {
        scanf("%d%d", &s, &t);
        bool mark = true;
        for(int j=s; j<=t; j++) {
            if(lef[j] >= s) {
                printf("No\n");
                mark = false;
                break;
            }
        }
        if(mark == true) {
            printf("Yes\n");
        }
    }
    return 0;
}

　　

靠，是因为查询的时候还是$O(n^2)$的啊。

哎，改改改

我们可以记录一个区间里的最大的la，哈哈哈哈

看下面，终于AC了

代码

#include <iostream>
#include <cstdio>
#define MAXN 1000007

using namespace std;

int N, Q, a[MAXN], s, t;

int lef[MAXN], la[MAXN], maxla[MAXN];

int main() {
	scanf("%d%d", &N, &Q);
	for(int i=1; i<=N; i++) {
		scanf("%d", &a[i]);
		lef[i] = la[a[i]];
		la[a[i]] = i;
		maxla[i] = max(maxla[i], lef[i]);
		maxla[i] = max(maxla[i], maxla[i-1]);
	}
	for(int i=1; i<=Q; i++) {
		scanf("%d%d", &s, &t);
		if(maxla[t] < s) printf("Yes\n");
		else printf("No\n");
	}
	return 0;
}