bzoj5483: [Usaco2018 Dec]Balance Beam

又又又又又又又被踩爆了

首先容易写出这样的期望方程：f(1)=max(d(1),f(2)/2)，f(n)=max(d(n),f(n-1)/2), f(i)=max(d(i),(f(i-1)+f(i+1))/2)，d是直接下来的收益

令S(i)等于后面那一个东西，那么f(i)=max(d(i),S(i))

套了max很难直接求，但是S(i)和d(i)一定是定值，那些由S贡献的点实际上就是被它左右两边各一个点的d贡献的，更确切的，假如把那些点是由d贡献找出来，那些由S贡献的点实际上就是被它左右两边第一个被d贡献的点贡献的

这样一来假设这两个点为L,R，则f(i)=x到L的概率*d(L)+x到R的概率*d(R)

考虑这样的一个子问题：数轴上0~n长度为n一段中，求由x走到n的概率

设g(i)表示i走到n的概率，则g(0)=0,g(n)=1,g(i)=(g(i-1)+g(i+1))/2，明显这个是个等差数列啊！

那么公差就是1/n，x走到n的概率就是x/n

x走到0，同理g(0)=1,g(n)=0,公差为-1/n，概率就是n-x/n

所以f(i)=((R-x)*d(L)+(x-L)*d(R))/(R-L)

现在问题就在于如何找到那些由d贡献的点了，我们在平面直角坐标系中把(i,d(i))标出来，则这些点就是凸包上的点

why？看图，如果我们要判断x是不是靠d贡献

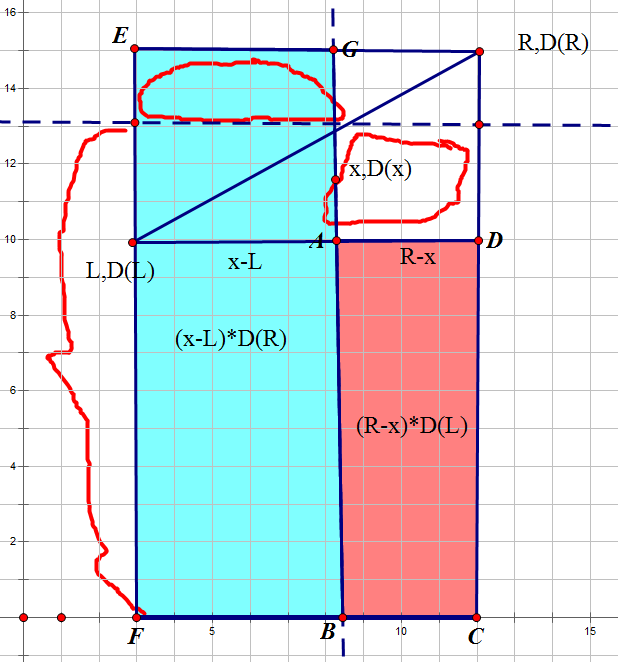
如图，((R-x)*d(L)+(x-L)*d(R))就是两个矩形的面积，容易发现两个圈画出来的面积是相等的，画出来的一段就是由L和R贡献出的S(x)，它就在L和R的直线上，是这条直线的自变量取x时的贡献！也就是说，这个点在直线下方，就意味着S(x)>d(x)，说明取d不如由L和R贡献。

完结撒花~~~

#include<cstdio>
#include<iostream>
#include<cstring>
#include<cstdlib>
#include<algorithm>
#include<cmath>
using namespace std;
typedef long long LL;
const int _=1e2;
const int maxn=1e5+_;

struct point{int x,y;}p[maxn];
LL multi(point p1,point p2,point p0)
{
    LL x1,y1,x2,y2;
    x1=p1.x-p0.x;
    y1=p1.y-p0.y;
    x2=p2.x-p0.x;
    y2=p2.y-p0.y;
    return x1*y2-x2*y1;
}
int top,sta[maxn];
int main()
{
    freopen("a.in","r",stdin);
    freopen("a.out","w",stdout);
    int n;
    scanf("%d",&n); sta[++top]=;
    for(int i=;i<=n;i++)
    {
        p[i].x=i,scanf("%d",&p[i].y);
        while(top>&&multi(p[sta[top]],p[i],p[sta[top-]])>=)top--;
        sta[++top]=i;
    }
    p[n+].x=n+;
    while(top>&&multi(p[sta[top]],p[n+],p[sta[top-]])>=)top--;
    sta[++top]=n+;

    int L=,R=;
    for(int i=;i<=n;i++)
    {
        while(L<top&&p[sta[L+]].x<=p[i].x)L++;
        if(p[sta[L]].x==p[i].x)
            printf("%lld\n",LL(p[i].y)*100000LL);
        else
        {
            while(R<top&&p[sta[R]].x<=p[i].x)R++;
            double d=(double(sta[R]-i)*double(p[sta[L]].y))/double(sta[R]-sta[L]) +
                     (double(i-sta[L])*double(p[sta[R]].y))/double(sta[R]-sta[L]);
            d*=;
            if(fabs(d-ceil(d))<=1e-)d+=1e-;
            printf("%.0lf\n",floor(d));
        }
    }

    return ;
}