数据结构实验4：C++实现循环队列

实验4

4.1 实验目的

熟练掌握队列的顺序存储结构和链式存储结构。

熟练掌握队列的有关算法设计，并在循环顺序队列和链队列上实现。

根据具体给定的需求，合理设计并实现相关结构和算法。

4.2 实验要求

4.2.1 循环顺序队列的实验要求

循环顺序队列结构和运算定义，算法的实现以库文件方式实现，不得在测试主程序中直接实现；

实验程序有较好可读性，各运算和变量的命名直观易懂，符合软件工程要求；

程序有适当的注释。

4.3 实验任务

4.3.1 循环顺序队列实验任务

编写算法实现下列问题的求解。

<1>初始化一个队列。

<2>判断是否队空。

<3>判断是否队满。

设队列最大长度：MaxLen=100

第一组数据：入队n个元素，判断队满

第二组数据：用循环方式将1到99，99个元素入队，判队满

<4>入队

第一组数据：4，7，8，12，20，50

第二组数据：a,b,c,d,f,g

<5>出队

<6>取队头元素

<7>求当前队列中元素个数

<8>编写算法实现

①初始化空循环队列；

②当键盘输入奇数时，此奇数入队；

③当键盘输入偶数时，队头出队；

④当键盘输入0时，算法退出；

⑤每当键盘输入后，输出当前队列中的所有元素。

4.5 运行结果截图及说明

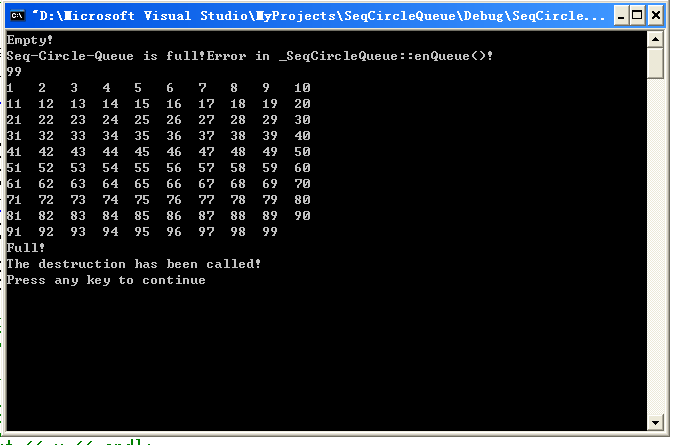
图1 测试（1）、（2）、（3）、（5）、（6）、（7）

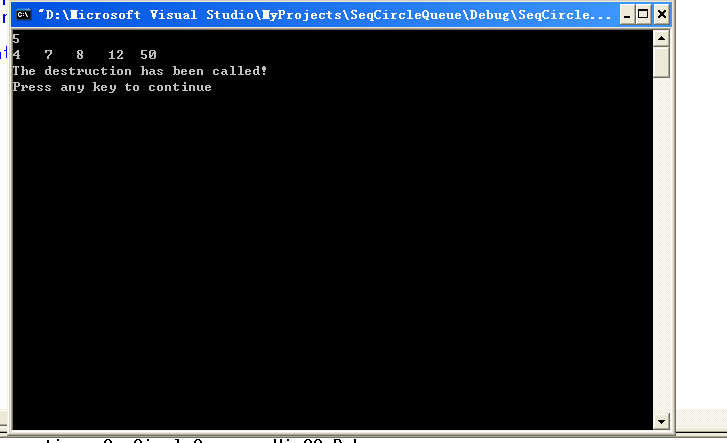
图2 测试（4）

图3 测试（4）

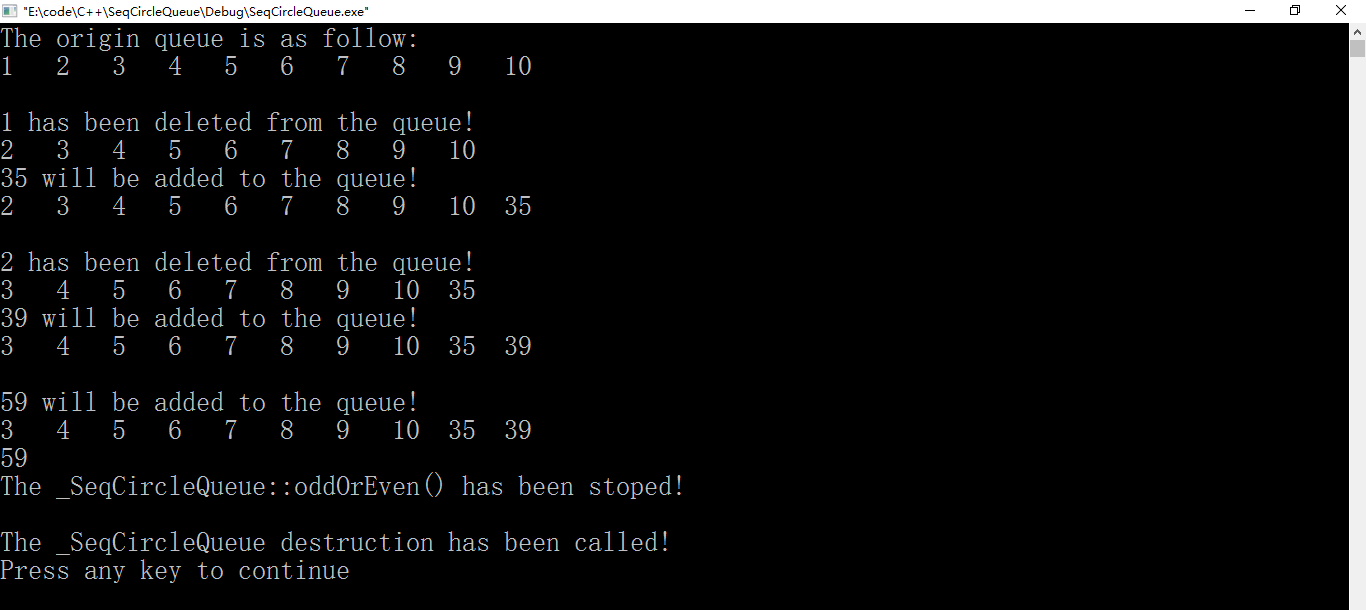
图4 测试（8）

4.6 附源代码

 // stdafx.h : include file for standard system include files,
 //  or project specific include files that are used frequently, but
 //      are changed infrequently
 //

 #if !defined(AFX_STDAFX_H__8FA49CDF_FC99_4984_AB37_46921F7ED357__INCLUDED_)
 #define AFX_STDAFX_H__8FA49CDF_FC99_4984_AB37_46921F7ED357__INCLUDED_

 #if _MSC_VER > 1000
 #pragma once
 #endif // _MSC_VER > 1000

 #include <stdc++.h>

 using namespace std;

 typedef int elementType;
 typedef char elementType1;
 const int maxn = ;

 // TODO: reference additional headers your program requires here

 //{{AFX_INSERT_LOCATION}}
 // Microsoft Visual C++ will insert additional declarations immediately before the previous line.

 #endif // !defined(AFX_STDAFX_H__8FA49CDF_FC99_4984_AB37_46921F7ED357__INCLUDED_)

 // _SeqCircleQueue.h: interface for the _SeqCircleQueue class.
 //
 //////////////////////////////////////////////////////////////////////

 #if !defined(AFX__SEQCIRCLEQUEUE_H__FCBC0603_27E1_4352_833C_6BED9B418B96__INCLUDED_)
 #define AFX__SEQCIRCLEQUEUE_H__FCBC0603_27E1_4352_833C_6BED9B418B96__INCLUDED_

 #if _MSC_VER > 1000
 #pragma once
 #endif // _MSC_VER > 1000

 class _SeqCircleQueue
 {
 public:
     _SeqCircleQueue();
     virtual ~_SeqCircleQueue();
     bool emptySeqCircleQueue();
     bool fullSeqCircleQueue();
     bool enQueue( elementType value );
     bool deQueue( elementType &value );
     bool getFront( elementType &value );
     int length();
     void oddOrEven( elementType value );
     friend ostream &operator<<( ostream &os, _SeqCircleQueue &scq )
     {
         if( ( scq._front -  ) % maxn == scq._rear )
             return os;
         int column  = ;
         for( int i = scq._front; i % maxn != scq._rear; i = ( i +  ) % maxn )
         {
             os << setw() << setiosflags(ios::left) << scq.data[i] << " ";
             column ++;
             if( column %  ==  )
                 os << endl;
         }
         os << endl;
     }
 private:
     elementType data[maxn];
     int _front;
     int _rear;

 };

 #endif // !defined(AFX__SEQCIRCLEQUEUE_H__FCBC0603_27E1_4352_833C_6BED9B418B96__INCLUDED_)

 // _SeqCircleQueue.cpp: implementation of the _SeqCircleQueue class.
 //
 //////////////////////////////////////////////////////////////////////

 #include "stdafx.h"
 #include "_SeqCircleQueue.h"

 //////////////////////////////////////////////////////////////////////
 // Construction/Destruction
 //////////////////////////////////////////////////////////////////////

 _SeqCircleQueue::_SeqCircleQueue()
 {
     _front = _rear = ;
 }

 _SeqCircleQueue::~_SeqCircleQueue()
 {
     ios::sync_with_stdio(false);
     cout << "The _SeqCircleQueue destruction has been called!" << endl;
 }

 bool _SeqCircleQueue::emptySeqCircleQueue()
 {
     return _front == _rear;
 } 

 bool _SeqCircleQueue::fullSeqCircleQueue()
 {
     return ( _rear +  ) % maxn == _front;
 }

 bool _SeqCircleQueue::enQueue( elementType value )
 {
     if( fullSeqCircleQueue() )
     {
         cerr << "Seq-Circle-Queue is full!Error in _SeqCircleQueue::enQueue()!" << endl;
         return false;
     }
     data[_rear] = value;
     _rear = ( _rear +  ) % maxn;
     return true;
 }

 bool _SeqCircleQueue::deQueue( elementType &value )
 {
     if( emptySeqCircleQueue() )
     {
         cerr << "Seq-Circle-Queue is empty!Error in _SeqCircleQueue::popFront()!" << endl;
         return false;
     }
     value = data[_front];
     _front = ( _front +  ) % maxn;
     return true;
 }

 bool _SeqCircleQueue::getFront( elementType &value )
 {
     if( emptySeqCircleQueue() )
     {
         cerr << "Seq-Circle-Queue is empty!Error in _SeqCircleQueue::getFront()!" << endl;
         return false;
     }
     value = data[_front];
     return true;
 }

 int _SeqCircleQueue::length()
 {
     if( emptySeqCircleQueue() )
     {
         cerr << "Seq-Circle-Queue is empty!Error in _SeqCircleQueue::length()!" << endl;
         return -;
     }
     return ( _rear - _front + maxn ) % maxn;
 }

 void _SeqCircleQueue::oddOrEven( elementType value )
 {
     if( value &  )
     {
         enQueue(value);
         cout << value << " will be added to the queue!" << endl;
         cout << (*this);
     }
     else if( !( value & ) && value !=  )
     {
         elementType x;
         deQueue(x);
         cout << x << " has been deleted from the queue!" << endl;
         cout << (*this);
     }
     else //if( value == 0 )
     {
         cout << "The _SeqCircleQueue::oddOrEven() has been stoped!" << endl;
         return;
     }
 }

 // charSeqCircleQueue.h: interface for the charSeqCircleQueue class.
 //
 //////////////////////////////////////////////////////////////////////

 #if !defined(AFX_CHARSEQCIRCLEQUEUE_H__FBB4F8DD_2EF9_43A6_8E23_FD7E4C56908E__INCLUDED_)
 #define AFX_CHARSEQCIRCLEQUEUE_H__FBB4F8DD_2EF9_43A6_8E23_FD7E4C56908E__INCLUDED_

 #if _MSC_VER > 1000
 #pragma once
 #endif // _MSC_VER > 1000

 class charSeqCircleQueue
 {
 public:
     charSeqCircleQueue();
     virtual ~charSeqCircleQueue();
     bool emptyCharSeqCircleQueue();
     bool fullCharSeqCircleQueue();
     bool enQueue( elementType1 value );
     bool deQueue( elementType1 &value );
     bool getFront( elementType1 &value );
     int length();
     friend ostream &operator<<( ostream &os, charSeqCircleQueue &cscq )
     {
         if( ( cscq._front -  ) % maxn == cscq._rear )
             return os;
         int column  = ;
         for( int i = cscq._front; i % maxn != cscq._rear; i = ( i +  ) % maxn )
         {
             os << setw() << setiosflags(ios::left) << cscq.data[i] << " ";
             column ++;
             if( column %  ==  )
                 os << endl;
         }
         os << endl;
     }
 private:
     elementType1 data[maxn];
     int _front;
     int _rear;

 };

 #endif // !defined(AFX_CHARSEQCIRCLEQUEUE_H__FBB4F8DD_2EF9_43A6_8E23_FD7E4C56908E__INCLUDED_)

 // charSeqCircleQueue.cpp: implementation of the charSeqCircleQueue class.
 //
 //////////////////////////////////////////////////////////////////////

 #include "stdafx.h"
 #include "charSeqCircleQueue.h"

 //////////////////////////////////////////////////////////////////////
 // Construction/Destruction
 //////////////////////////////////////////////////////////////////////

 charSeqCircleQueue::charSeqCircleQueue()
 {
     _front = _rear = ;
 }

 charSeqCircleQueue::~charSeqCircleQueue()
 {
     ios::sync_with_stdio(false);
     cout << "The charSeqCircleQueue destruction has been called!" << endl;
 }

 bool charSeqCircleQueue::emptyCharSeqCircleQueue()
 {
     return _front == _rear;
 } 

 bool charSeqCircleQueue::fullCharSeqCircleQueue()
 {
     return ( _rear +  ) % maxn == _front;
 }

 bool charSeqCircleQueue::enQueue( elementType1 value )
 {
     if( fullCharSeqCircleQueue() )
     {
         cerr << "Seq-Circle-Queue is full!Error in charSeqCircleQueue::::enQueue()!" << endl;
         return false;
     }
     data[_rear] = value;
     _rear = ( _rear +  ) % maxn;
     return true;
 }

 bool charSeqCircleQueue::deQueue( elementType1 &value )
 {
     if( emptyCharSeqCircleQueue() )
     {
         cerr << "Seq-Circle-Queue is empty!Error in charSeqCircleQueue::popFront()!" << endl;
         return false;
     }
     value = data[_front];
     _front = ( _front +  ) % maxn;
     return true;
 }

 bool charSeqCircleQueue::getFront( elementType1 &value )
 {
     if( emptyCharSeqCircleQueue() )
     {
         cerr << "Seq-Circle-Queue is empty!Error in charSeqCircleQueue::::getFront()!" << endl;
         return false;
     }
     value = data[_front];
     return true;
 }

 int charSeqCircleQueue::length()
 {
     if( emptyCharSeqCircleQueue() )
     {
         cerr << "Seq-Circle-Queue is empty!Error in charSeqCircleQueue::::length()!" << endl;
         return -;
     }
     return ( _rear - _front + maxn ) % maxn;
 }

4.7 调试过程中出现的bug总结

注意细节！