洛谷——P3384 【模板】树链剖分

https://www.luogu.org/problem/show?pid=3384#sub

题目描述

如题，已知一棵包含N个结点的树（连通且无环），每个节点上包含一个数值，需要支持以下操作：

操作1：格式： 1 x y z 表示将树从x到y结点最短路径上所有节点的值都加上z

操作2：格式： 2 x y 表示求树从x到y结点最短路径上所有节点的值之和

操作3：格式： 3 x z 表示将以x为根节点的子树内所有节点值都加上z

操作4：格式： 4 x 表示求以x为根节点的子树内所有节点值之和

输入输出格式

输入格式：

第一行包含4个正整数N、M、R、P，分别表示树的结点个数、操作个数、根节点序号和取模数（即所有的输出结果均对此取模）。

接下来一行包含N个非负整数，分别依次表示各个节点上初始的数值。

接下来N-1行每行包含两个整数x、y，表示点x和点y之间连有一条边（保证无环且连通）

接下来M行每行包含若干个正整数，每行表示一个操作，格式如下：

操作1： 1 x y z

操作2： 2 x y

操作3： 3 x z

操作4： 4 x

输出格式：

输出包含若干行，分别依次表示每个操作2或操作4所得的结果（对P取模）

输入输出样例

输入样例#1：

输出样例#1：

2

21

说明

时空限制：1s，128M

数据规模：

对于30%的数据：N<=10，M<=10

对于70%的数据：N<=1000，M<=1000

对于100%的数据：N<=100000，M<=100000

（其实，纯随机生成的树LCA+暴力是能过的，可是，你觉得可能是纯随机的么233）

样例说明：

树的结构如下：

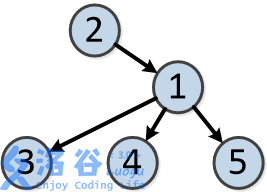
各个操作如下：

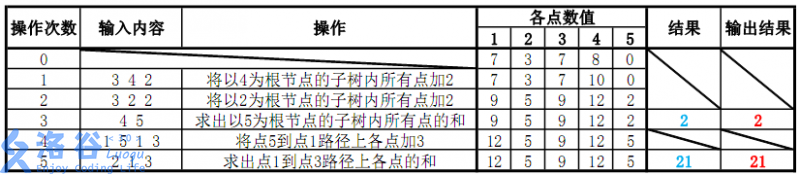
故输出应依次为2、21(重要的事情说三遍：记得取模)

 #include <algorithm>

 #include <cstdio>

 using namespace std;

 const int N(+);

 const int M(+);

 int n,m,rt,mod,u,v,w,op,val[N];

 int head[N],sumedge;

 struct Edge

 {

     int u,v,next;

     Edge(int u=,int v=,int next=):

         u(u),v(v),next(next){}

 }edge[M<<];

 void ins(int u,int v)

 {

     edge[++sumedge]=Edge(u,v,head[u]);

     head[u]=sumedge;

 }

 int deep[N],dad[N],son[N],size[N],top[N],dfn[N],id[N],cnt;

 /*void DFS(int u,int father,int deepth)

 {

     deep[u]=deepth;

     dad[u]=father;

     size[u]=1;

     son[u]=0;

     for(int i=head[u];i;i=edge[i].next)

     {

         int to=edge[i].v;

         if(dad[u]==to) continue;

         DFS(to,u,deepth+1);    size[u]+=size[to];

         if(!son[u]||size[son[u]]<size[to]) son[u]=to;

     }

 }

 void DFS_(int u,int Top)

 {

     top[u]=Top;

     id[u]=++cnt;

     dfn[cnt]=u;

     if(son[u]) DFS_(son[u],Top);

     for(int i=head[u];i;i=edge[i].next)

     {

         int to=edge[i].v;

         if(to!=dad[u]&&to!=son[u]) DFS_(to,to);

     }

 }*/

 void DFS(int x)

 {

     size[x]=;deep[x]=deep[dad[x]]+;

     for(int i=head[x];i;i=edge[i].next)

     {

         int to=edge[i].v;

         if(dad[x]!=to)

         {

             dad[to]=x;

             DFS(to);

             size[x]+=size[to];

         }

     }

 }

 void DFS_(int x)

 {

     id[x]=++cnt;dfn[cnt]=x;

     int t=;if(!top[x]) top[x]=x;

     for(int i=head[x];i;i=edge[i].next)

     {

         int to=edge[i].v;

         if(dad[x]!=to&&size[t]<size[to]) t=to;

     }

     if(t) top[t]=top[x],DFS_(t);

     for(int i=head[x];i;i=edge[i].next)

     {

         int to=edge[i].v;

         if(dad[x]!=to&&t!=to) DFS_(to);

     }

 }

 struct Tree

 {

     int l,r,flag,val,mid;

 }tree[M<<];

 void Tree_up(int now)

 {

     tree[now].val=tree[now<<].val+tree[now<<|].val;

 }

 void Tree_down(int now)

 {

     tree[now<<].flag+=tree[now].flag;

     tree[now<<].val=(tree[now<<].val+(tree[now].mid-tree[now].l+)*tree[now].flag)%mod;

     tree[now<<|].flag+=tree[now].flag;

     tree[now<<|].val=(tree[now<<|].val+(tree[now].r-tree[now].mid)*tree[now].flag)%mod;

     tree[now].flag=;

 }

 void Tree_build(int now,int l,int r)

 {

     tree[now].l=l,tree[now].r=r;

     if(l==r)

     {

         tree[now].val=val[dfn[l]];

         return ;

     }

     tree[now].mid=tree[now].l+tree[now].r>>;

     Tree_build(now<<,l,tree[now].mid);

     Tree_build(now<<|,tree[now].mid+,r);

     Tree_up(now);

 }

 void Tree_change(int now,int l,int r,int x)

 {

     if(tree[now].l==l&&tree[now].r==r)

     {

         tree[now].flag+=x;

         tree[now].val=(tree[now].val+(tree[now].r-tree[now].l+)*x)%mod;

         return ;

     }

     if(tree[now].flag)    Tree_down(now);

     if(tree[now].mid>=r)    Tree_change(now<<,l,r,x);

     else if(tree[now].mid<l)    Tree_change(now<<|,l,r,x);

     else

     {

         Tree_change(now<<,l,tree[now].mid,x);

         Tree_change(now<<|,tree[now].mid+,r,x);

     }

     Tree_up(now);

 }

 int Tree_query(int now,int l,int r)

 {

     if(tree[now].flag) Tree_down(now);

     if(tree[now].l==l&&tree[now].r==r)

         return tree[now].val%mod;

     if(tree[now].mid>=r) return Tree_query(now<<,l,r);

     else if(tree[now].mid<l) return Tree_query(now<<|,l,r);

     else return (Tree_query(now<<,l,tree[now].mid)+Tree_query(now<<|,tree[now].mid+,r))%mod;

 }

 void List_change(int x,int y,int z)

 {

     for(;top[x]!=top[y];x=dad[top[x]])

     {

         if(deep[top[x]]<deep[top[y]]) swap(x,y);

         Tree_change(,id[top[x]],id[x],z);

     }

     if(deep[x]<deep[y]) swap(x,y);

     Tree_change(,id[y],id[x],z);

 }

 int List_query(int x,int y)

 {

     int ret=;

     for(;top[x]!=top[y];x=dad[top[x]])

     {

         if(deep[top[x]]<deep[top[y]]) swap(x,y);

         ret=(ret+Tree_query(,id[top[x]],id[x]))%mod;

     }

     if(deep[x]<deep[y]) swap(x,y);

     ret=(ret+Tree_query(,id[y],id[x]))%mod;

     return ret;

 }

 int main()

 {

     scanf("%d%d%d%d",&n,&m,&rt,&mod);

     for(int i=;i<=n;i++) scanf("%d",val+i);

     for(int i=;i<n;i++)

         scanf("%d%d",&u,&v),ins(u,v),ins(v,u);

     DFS(rt); DFS_(rt);

 //    DFS(rt,0,1);DFS_(rt,rt);

     Tree_build(,,n);

     for(;m--;)

     {

         scanf("%d",&op);

         if(op==)

         {

             scanf("%d%d%d",&u,&v,&w);

             List_change(u,v,w);

         }

         else if(op==)

         {

             scanf("%d%d",&u,&v);

             printf("%d\n",List_query(u,v));

         }

         else if(op==)

         {

             scanf("%d%d",&u,&w);

             Tree_change(,id[u],id[u]+size[u]-,w);

         }

         else

         {

             scanf("%d",&u);

             printf("%d\n",Tree_query(,id[u],id[u]+size[u]-));

         }

     }

     return ;

 }