[机器学习]Generalized Linear Model

　　最近一直在回顾linear regression model和logistic regression model，但对其中的一些问题都很疑惑不解，知道我看到广义线性模型即Generalized Linear Model后才恍然大悟原来这些模型是这样推导的，在这里与诸位分享一下，具体更多细节可以参考Andrew Ng的课程。

　　一、指数分布

　　广义线性模型都是由指数分布出发来推导的，所以在介绍GLM之前先讲讲什么是指数分布。指数分布的形式如下：

　　　　　　　　　　　　　　　　　

　　η是参数，T(y)是y的充分统计量，即T(y)可以完全表达y，通常T(y)=y。当参数T，b，a都固定的时候，就定义了一个以η为参数的参数簇。实际上，很多的概率分布都是属于指数分布，比如：

　　（1）伯努利分布

　　（2）正态分布

　　（3）泊松分布

　　（4）伽马分布

　　等等等。。。。

　　或许从原本的形式上看不出来他们是指数分布，但是经过一系列的变换之后，就会发现他们都是指数分布。举两个例子，顺便我自己也推导一下。

　　伯努利分布：

　　

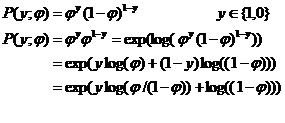
　　那么b(y)=1,T(y)=y,η=log(φ/(1-φ)),a(η)=log((1-φ))，则φ=1/(1+e^-y)，这个就是sigmoid函数的由来。

　　同样我们对正态分布做变换，不过在这里我们要假设方差为1，以为方差并不影响我们的回归。

　　

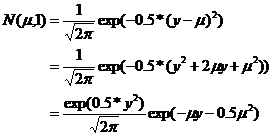
　　我们可以看到η=µ。

　　

　　二、广义线性模型

　　介绍完指数分布后我们可以来看看广义线性模型是怎样的。

　　首先广义线性模型有三个假设，这三个假设即是前提条件也是帮助我们构造模型的关键。

　　（1）P(y|x;θ)~ExpFamliy(η);

　　（2）对于一个给定x，我们的目标函数为h(x)=E[T(y)|x];

　　（3）η=Θ^Tx

　　根据以上三个假设我们就能推导出logistic model 和 最小二乘模型。Logistic model 推导如下：

　　　　　　h(x)=E[T(y)|x]=E[y|x]=φ=1/(1+e^-η)=1/(1+e^-ΘTx)

　　对于最小二乘模型推导如下：

　　　　　　h(x)=E[T(y)|x]=E[y|x]=η=µ=Θ^Tx

　　从中我们将把η和原模型参数联系起来的函数称之为正则响应函数。所以对于广义线性模型，我们需要y是怎样的分布，就能推导出相应的模型。有兴趣的可以从多项式分布试试推导出SoftMax回归。