洛谷 P3576 [POI2014]MRO-Ant colony

P3576 [POI2014]MRO-Ant colony

题目描述

The ants are scavenging an abandoned ant hill in search of food.

The ant hill has nn chambers and n-1n−1 corridors connecting them.

We know that each chamber can be reached via a unique path from every other chamber.

In other words, the chambers and the corridors form a tree.

There is an entrance to the ant hill in every chamber with only one corridor leading into (or out of) it.

At each entry, there are gg groups of m_1,m_2,\cdots,m_gm​1​​,m​2​​,⋯,m​g​​ ants respectively.

These groups will enter the ant hill one after another, each successive group entering once there are no ants inside.

Inside the hill, the ants explore it in the following way:

• Upon entering a chamber with dd outgoing corridors yet unexplored by the group,the group divides into dd groups of equal size. Each newly created group follows one of the d corridors.If d=0d=0, then the group exits the ant hill.

• If the ants cannot divide into equal groups, then the stronger ants eat the weaker until a perfect division is possible.Note that such a division is always possible since eventually the number of ants drops down to zero.Nothing can stop the ants from allowing divisibility - in particular, an ant can eat itself, and the last one remaining will do so if the group is smaller than dd.

The following figure depicts mm ants upon entering a chamber with three outgoing unexplored corridors, dividing themselves into three (equal) groups of \left \lfloor m/3 \right \rfloor⌊m/3⌋ ants each.

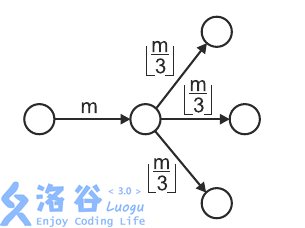
A hungry anteater dug into one of the corridors and can now eat all the ants passing through it.

However, just like the ants, the anteater is very picky when it comes to numbers.

It will devour a passing group if and only if it consists of exactly kk ants.

We want to know how many ants the anteater will eat.

给一棵树，对于每个叶子节点，都有g群蚂蚁要从外面进来，每群蚂蚁在行进过程中只要碰到岔路，就将平均地分成岔路口数-1那么多份，然后平均地走向剩下的那些岔路口，余下的蚂蚁自动消失，树上有一个关键边，假如有一群蚂蚁通过了这条边且数量恰好为k，这k只蚂蚁就被吃掉，问一共有多少只蚂蚁被吃掉

输入输出格式

输入格式：

The first line of the standard input contains three integers nn, gg, kk(2\le n,g\le 1\ 000\ 0002≤n,g≤1 000 000, 1\le k\le 10^91≤k≤10​9​​), separated by single spaces.

These specify the number of chambers, the number of ant groups and the number of ants the anteater devours at once. The chambers are numbered from 1 to nn.

The second line contains gg integers m_1,m_2,\cdots,m_gm​1​​,m​2​​,⋯,m​g​​ (1\le m_i\le 10^91≤m​i​​≤10​9​​), separated by single spaces, where m_im​i​​ gives the number of ants in the ii-th group at every entrance to the ant hill. The n-1n−1 lines that follow describe the corridors within the ant hill;the ii-th such line contains two integers a_ia​i​​,b_ib​i​​ (1\le a_i,b_i\le n1≤a​i​​,b​i​​≤n), separated by a single space, that indicate that the chambers no. a_ia​i​​ and b_ib​i​​ are linked by a corridor. The anteater has dug into the corridor that appears first on input.

输出格式：

Your program should print to the standard output a single line containing a single integer: the number of ants eaten by the anteater.

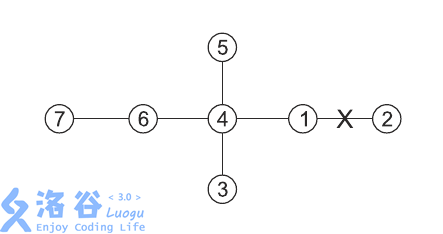
输入输出样例

输入样例#1：

7 5 3
3 4 1 9 11
1 2
1 4
4 3
4 5
4 6
6 7

输出样例#1：

21

说明

给一棵树，对于每个叶子节点，都有g群蚂蚁要从外面进来，每群蚂蚁在行进过程中只要碰到岔路，就将平均地分成岔路口数-1那么多份，然后平均地走向剩下的那些岔路口，余下的蚂蚁自动消失，树上有一个关键边，假如有一群蚂蚁通过了这条边且数量恰好为k，这k只蚂蚁就被吃掉，问一共有多少只蚂蚁被吃掉

题意：

题目描述：

给定一棵有n个节点的树。在每个叶子节点，有g群蚂蚁要从外面进来，其中第i群有m[i]只蚂蚁。这些蚂蚁会相继进入树中，而且要保证每一时刻每个节点最多只有一群蚂蚁。这些蚂蚁会按以下方式前进：

·在即将离开某个度数为d+1的点时，该群蚂蚁有d个方向还没有走过，这群蚂蚁就会分裂成d群，每群数量都相等。如果d=0，那么蚂蚁会离开这棵树。

·如果蚂蚁不能等分，那么蚂蚁之间会互相吞噬，直到可以等分为止，即一群蚂蚁有m只，要分成d组，每组将会有floor(m/d)只，如下图。

一只饥饿的食蚁兽埋伏在一条边上，如果有一群蚂蚁通过这条边，并且数量恰为k只，它就会吞掉这群蚂蚁。请计算一共有多少只蚂蚁会被吞掉。

输入描述：

第一行包含三个整数n,g,k,表示点数、蚂蚁群数以及k。

第二行包含g个整数m[1],m[2],...,m[g]，表示每群蚂蚁中蚂蚁的数量。

接下来n-1行每行两个整数，表示一条边，食蚁兽埋伏在输入的第一条边上。

思路：

这个题从叶子节点去算的话显然很困难，所以我们可以从食蚁兽所在的两个点开始倒着搞。

 minn和maxn记录每个节点最多和最少有多少个蚂蚁才能让食蚁兽恰好吃到k只。然后，分别以这两个点为根节点，dfs一下求出所有的minn和maxn。 

接着，二分答案，求一下对于每个节点,g群蚂蚁中符合条件的蚂蚁的群数。

最后，群数*k即为所求。

#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
#define MAXN 1000001
using namespace std;
int n,g,K;
int s,t,tot;
long long ans;
int outo[MAXN],dad[MAXN];
int to[MAXN],net[MAXN],head[MAXN];
long long m[MAXN],minn[MAXN],maxn[MAXN];
void add(int u,int v){
    to[++tot]=v;net[tot]=head[u];head[u]=tot;
    to[++tot]=u;net[tot]=head[v];head[v]=tot;
}
void dfs(int now){
    for(int i=head[now];i;i=net[i])
        if(dad[now]!=to[i]){
            dad[to[i]]=now;
            outo[now]++;
        }
    for(int i=head[now];i;i=net[i])
        if(dad[now]!=to[i]){
            minn[to[i]]=minn[now]*outo[now];
            maxn[to[i]]=(maxn[now]+)*outo[now]-;
            maxn[to[i]]=min(maxn[to[i]],m[g]);
            if(minn[to[i]]<=m[g])
                dfs(to[i]);
        }
}
long long cal(long long  x){
    int l=,r=g,bns=;
    while(l<=r){
        int mid=(l+r)/;
        if(m[mid]<x){
            bns=max(bns,mid);
            l=mid+;
        }
        else r=mid-;
    }
    return bns;
}
int main(){
    scanf("%d%d%d",&n,&g,&K);
    for(int i=;i<=g;i++)    scanf("%d",&m[i]);
    sort(m+,m++g);
    scanf("%d%d",&s,&t);
    for(int i=;i<n;i++){
        int x,y;
        scanf("%d%d",&x,&y);
        add(x,y);
    }
    minn[s]=maxn[s]=minn[t]=maxn[t]=K;
    dfs(s);
    dfs(t);
    for(int i=;i<=n;i++)
        if(!outo[i])
            ans+=cal(maxn[i]+)-cal(minn[i]);
    cout<<ans*K;
}