HDU - 2196（树形DP）

题目：

A school bought the first computer some time ago(so this computer's id is 1). During the recent years the school bought N-1 new computers. Each new computer was connected to one of settled earlier. Managers of school are anxious about slow functioning of the net and want to know the maximum distance Si for which i-th computer needs to send signal (i.e. length of cable to the most distant computer). You need to provide this information. 

Hint: the example input is corresponding to this graph. And from the graph, you can see that the computer 4 is farthest one from 1, so S1 = 3. Computer 4 and 5 are the farthest ones from 2, so S2 = 2. Computer 5 is the farthest one from 3, so S3 = 3. we also get S4 = 4, S5 = 4.

InputInput file contains multiple test cases.In each case there is natural number N (N<=10000) in the first line, followed by (N-1) lines with descriptions of computers. i-th line contains two natural numbers - number of computer, to which i-th computer is connected and length of cable used for connection. Total length of cable does not exceed 10^9. Numbers in lines of input are separated by a space.OutputFor each case output N lines. i-th line must contain number Si for i-th computer (1<=i<=N).Sample Input

5
1 1
2 1
3 1
1 1

Sample Output

2
3
4
4

题意：
　　不知道多少组测试样例，第一行一个n，代表有多少台电脑，接下来有n-1行，每行两个数a，b，第i行（2<=i<=n）表示编号为i的电脑连接编号为a的电脑，他们的距离是b（即电缆长度），问每台电脑到其最远点距离

思路：树形DP（感谢大佬的视频讲解 https://www.bilibili.com/video/av12194537?t=1863）
我们定义f【i】表示编号为i的节点第一步向儿子方向走的最远距离
　　　　g【i】表示编号为i的节点第一步向父亲方向走的最远距离
　　　　p【i】表示编号为i的节点的父亲节点编号
　　　　w（a，b）表示编号a节点到编号b节点的距离，a和b是一条边连接的，即边权
用2个dfs求出这三个数组
递推式：f【u】=max（f【v】，w（u，v））//v是u的孩子
　　　　g【u】=w(u，p【u】)+max(g【p【u】】,f【v】+w（p【u】，u）)//v是u的兄弟
两个递推式在下面讲解
对于第i个节点，答案就是max（f【i】，g【i】）
因为对一个节点来说，它的第一步只能是向孩子方向走（可能有多个孩子）或者向父亲方向走

第一遍dfs求出f和p数组，我们默认1节点是根节点，它的父亲节点是0（假想）
这个深搜很容易理解，直接上代码

long long int dfs1(int u,int fa)
{//u节点走孩子方向的最大距离
    for(int i=;i<E[u].size();++i){
        int v=E[u][i].first;
        int w=E[u][i].second;
        if(v!=fa)
        f[u]=max(f[u],dfs1(v,p[v]=u)+w);
/*要么是当前值（可能有多个孩子），要么是当前点到孩子点的距离加上f【v】*/
    }
    return f[u];
}

第二遍dfs求出g数组，看图（假设边权都为1）

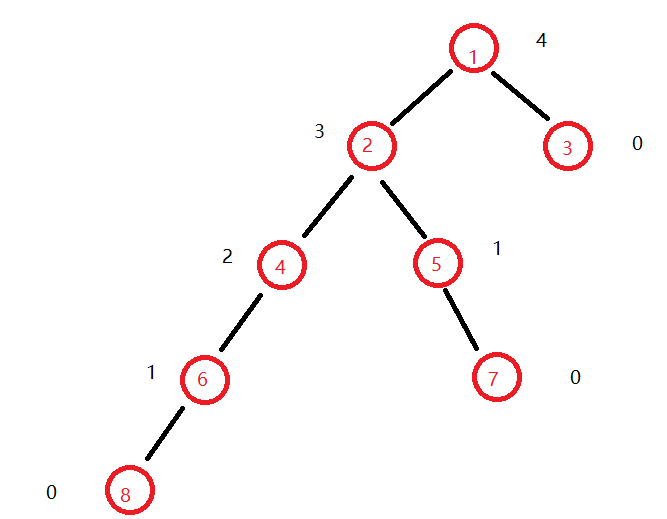
图中红色数字为节点编号，黑色数字表示f【u】的值(第一遍dfs求出)，即当前节点第一步向孩子方向走的最大距离

第一遍dfs，相当于从下往上进行动态规划，而第二遍dfs，则是从上往下进行动态规划

怎么用f和p数组算出g数组呢

假设我们要求节点u的g，令fa是u节点的父亲节点

首先，g【u】=g【fa】（假设第一步往上走且第二步也是往上走的距离最大）

然后遍历fa连接的所有节点

若找到fa的父亲节点，跳过，因为我们一开始就假设走这条路

若找到u节点，跳过，跑回来干嘛

若找到其他节点（必然为u节点的兄弟节点，我们设为v，v可能有多个，也可能没有）

则比较g【u】和w（fa，v）+f【v】的大小，即比较第二步往上走好一点还是往下走好一点

遍历完之后，g【u】加上w（fa，u），就成功把g【u】算出来了

我们看出，要想求g【u】，就要先知道g【fa】，即要先知道上面节点的g，才能求下面节点的g

所以，这是一个从上往下走的过程

对于根节点的计算，我们不存在w（0,1）所以还要注意一下边界问题

代码实现：

void dfs2(int u,int fa)
{
    int t=;
    g[u]=g[fa];
    for(int i=;i<E[fa].size();++i){
        int v=E[fa][i].first;
        int w=E[fa][i].second;
        if(v==p[fa]) continue;//fa的父亲节点，跳过
        if(v==u) t=w;//又跑回来了，跳过
        else g[u]=max(g[u],f[v]+w);//更新
    }
    g[u]+=t;
    for(int i=;i<E[u].size();++i){//dfs孩子节点，更新下面的g
        int v=E[u][i].first;
        int w=E[u][i].second;
        if(v!=fa) dfs2(v,u);
    }
}

我们模拟跑一下dfs2，从根节点开始

首先g【1】=g【0】=0；然后编号0节点是虚拟的，没有连接任何点，所以g【1】=0；

求节点2，g【2】=g【1】=0；然后遍历编号1节点连接的所有点

找到节点2，跳过，找到节点3，更新g【2】=max（g【2】，w（1,3）+f【3】）=max（0,1+0）=1；

遍历完后，我们加上w（1,2）=1，所以g【2】=1+1=2；

求节点4，g【4】=g【2】=2；然后遍历编号2节点连接的所有点

找到节点1,1是2的父亲节点，跳过

找到节点4，跳过

找到节点5，更新g【4】=max（g【4】，w（2,5）+f【5】）=max（2,1+1）=2；

遍历完后，我们加上w（2,4）=1，所以g【4】=2+1=3；

......

这样就更新好了g数组

然后答案就是max（f【i】，g【i】）啦，第一步要么向孩子方向走，要么向父亲方向走，找二者最大就行了

完整代码：

#include <bits/stdc++.h>
#define mp make_pair
using namespace std;
typedef long long int ll;
const int maxn=1e5+;
vector<pair<int,int> > E[maxn];
long long int f[maxn],g[maxn],p[maxn];
long long int dfs1(int u,int fa)
{//u节点走孩子方向的最大距离
    for(int i=;i<E[u].size();++i){
        int v=E[u][i].first;
        int w=E[u][i].second;
        if(v!=fa)
        f[u]=max(f[u],dfs1(v,p[v]=u)+w);
    }
    return f[u];
}
void dfs2(int u,int fa)
{
    int t=;
    g[u]=g[fa];
    for(int i=;i<E[fa].size();++i){
        int v=E[fa][i].first;
        int w=E[fa][i].second;
        if(v==p[fa]) continue;
        if(v==u) t=w;
        else g[u]=max(g[u],f[v]+w);
    }
    g[u]+=t;
    for(int i=;i<E[u].size();++i){
        int v=E[u][i].first;
        int w=E[u][i].second;
        if(v!=fa) dfs2(v,u);
    }
}

int main()
{
    int n;
    while(cin>>n)
    {
        for(int i=;i<=n;++i)
        E[i].clear();
        memset(f,,sizeof(f));
        memset(g,,sizeof(g));
        memset(p,,sizeof(p));
        for(int i=;i<=n;++i){
            int a,b;
            scanf("%d%d",&a,&b);
            E[a].push_back(mp(i,b));
            E[i].push_back(mp(a,b));
        }
        dfs1(,);
        dfs2(,);
        for(int i=;i<=n;++i){
            printf("%lld\n",max(f[i],g[i]));
        }
    }
    return ;
}