Noip2011 提高组 Day1 T1 铺地毯 + Day2 T1 计算系数

Day1 T1

题目描述

为了准备一个独特的颁奖典礼，组织者在会场的一片矩形区域（可看做是平面直角坐标系的第一象限）铺上一些矩形地毯。一共有 n 张地毯，编号从 1 到n 。现在将这些地毯按照编号从小到大的顺序平行于坐标轴先后铺设，后铺的地毯覆盖在前面已经铺好的地毯之上。

地毯铺设完成后，组织者想知道覆盖地面某个点的最上面的那张地毯的编号。注意：在矩形地毯边界和四个顶点上的点也算被地毯覆盖。

输入输出格式

输入格式：

输入文件名为carpet.in 。

输入共n+2 行。

第一行，一个整数n ，表示总共有 n 张地毯。

接下来的n 行中，第 i+1 行表示编号i 的地毯的信息，包含四个正整数 a ，b ，g ，k ，每两个整数之间用一个空格隔开，分别表示铺设地毯的左下角的坐标（a ，b ）以及地毯在x轴和y 轴方向的长度。

第n+2 行包含两个正整数 x 和y，表示所求的地面的点的坐标（x ，y）。

输出格式：

输出文件名为carpet.out 。

输出共1 行，一个整数，表示所求的地毯的编号；若此处没有被地毯覆盖则输出-1 。

输入输出样例

输入样例#1：

3
1 0 2 3
0 2 3 3
2 1 3 3
2 2

输出样例#1：

3

输入样例#2：

3
1 0 2 3
0 2 3 3
2 1 3 3
4 5

输出样例#2：

-1

说明

【样例解释1】

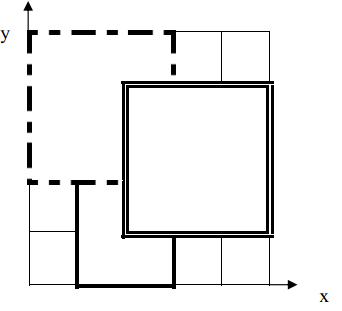
如下图，1 号地毯用实线表示，2 号地毯用虚线表示，3 号用双实线表示，覆盖点（2,2）的最上面一张地毯是 3 号地毯。

【数据范围】

对于30% 的数据，有 n ≤2 ；

对于50% 的数据，0 ≤a, b, g, k≤100；

对于100%的数据，有 0 ≤n ≤10,000 ，0≤a, b, g, k ≤100,000。

noip2011提高组day1第1题

思路:

　　输入数据直接进行模拟即可

坑点:

　　要搞清楚a,b,g,k具体代表着什么

上代码:

#include <iostream>
#include <cstdio>
using namespace std;

const int M = ;
int n,x0,y0,ans;
bool flag;
struct node {
    int x,y,r,c;
}e[M]; 

int main() {
    scanf("%d",&n);
    for(int i=; i<=n; i++) scanf("%d%d%d%d",&e[i].x,&e[i].y,&e[i].r,&e[i].c);
    scanf("%d%d",&x0,&y0);
    for(int i=n,xl,xr,yl,yr; i>; i--) {
        xl=e[i].x,xr=e[i].x+e[i].r,yl=e[i].y,yr=e[i].y+e[i].c;
        if(xl<=x0&&x0<=xr && yl<=y0&&y0<=yr) {
            ans=i;
            flag=true;
            break;
        }
    }
    if(flag) printf("%d",ans);
    else printf("-1");
    return ;
} 

---

Day2 T1

题目描述

给定一个多项式(by+ax)^k，请求出多项式展开后x^n*y^m 项的系数。

输入输出格式

输入格式：

输入文件名为factor.in。

共一行，包含5 个整数，分别为 a ，b ，k ，n ，m，每两个整数之间用一个空格隔开。

输出格式：

输出共1 行，包含一个整数，表示所求的系数，这个系数可能很大，输出对10007 取模后的结果。

输入输出样例

输入样例#1：

1 1 3 1 2

输出样例#1：

3

说明

【数据范围】

对于30% 的数据，有 0 ≤k ≤10 ；

对于50% 的数据，有 a = 1，b = 1；

对于100%的数据，有 0 ≤k ≤1,000，0≤n, m ≤k ，且n + m = k ，0 ≤a ，b ≤1,000,000。

noip2011提高组day2第1题

思路:

　　用二项式定理以及模拟来解决此题

坑点:

　　需要用到快速幂...被自己的快速幂蠢哭了qwq,愣是没看出来....下次再错就....下一顿饭不吃了!(超级狠

上代码:

#include <iostream>
#include <cstdio>
#define LL long long
using namespace std;

const int Mod = ;
int k,n,m,a,b;
int C[][];

LL ksm(LL q,LL p) {
    LL r=;
    for(; p; p>>=) {
        if(p&) r=r*q%Mod;
        q=q*q%Mod; //这里是q=q*q%Mod ,不是r=r*r%Mod....
    }
    return r;
}

int main() {
    scanf("%d%d%d%d%d",&a,&b,&k,&n,&m);
    C[][]=;
    for(int i=; i<=k; i++) C[i][]=C[i][i]=;
    for(int i=; i<=k; i++)
        for(int j=; j<i; j++)
            C[i][j]=(C[i-][j]+C[i-][j-])%Mod;
    cout<<C[k][m]*ksm(a,n)*ksm(b,m)%Mod;
    return ;
}