概率DP（放棋子）Domination

题意：https://zoj.pintia.cn/problem-sets/91827364500/problems/91827369874

给你n*m的棋盘，我们定义放满棋盘是：任意一行一列至少有一个棋子。

问你放满棋盘需要棋子的期望数。

思路：

我们先算出用x个棋子放满棋盘的概率，然后求Sigma就可以了

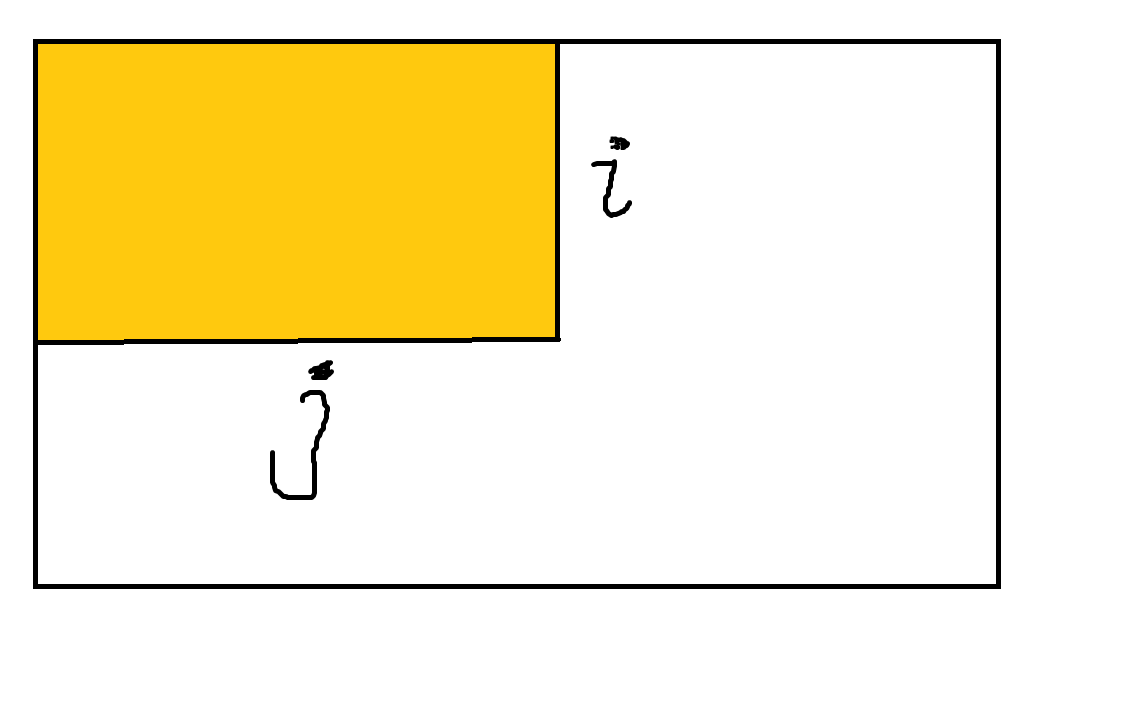
我们可以转换一下放棋子的方式，在任意一个地方放棋子，我们都可以把这个位置尽可能的移到左上角。

dp【k】【i】【j】是放了k个棋子，已经有 i 行 j 列满了的概率；

注意：放最后一个的时候不需要加放在 i，j区域里的概率（既然都放里面了，那就已经放满了）。

 #define IOS ios_base::sync_with_stdio(0); cin.tie(0);
 #include <cstdio>//sprintf islower isupper
 #include <cstdlib>//malloc  exit strcat itoa system("cls")
 #include <iostream>//pair
 #include <fstream>//freopen("C:\\Users\\13606\\Desktop\\草稿.txt","r",stdin);
 #include <bitset>
 //#include <map>
 //#include<unordered_map>
 #include <vector>
 #include <stack>
 #include <set>
 #include <string.h>//strstr substr
 #include <string>
 #include <time.h>//srand(((unsigned)time(NULL))); Seed n=rand()%10 - 0~9;
 #include <cmath>
 #include <deque>
 #include <queue>//priority_queue<int, vector<int>, greater<int> > q;//less
 #include <vector>//emplace_back
 //#include <math.h>
 //#include <windows.h>//reverse(a,a+len);// ~ ! ~ ! floor
 #include <algorithm>//sort + unique : sz=unique(b+1,b+n+1)-(b+1);+nth_element(first, nth, last, compare)
 using namespace std;//next_permutation(a+1,a+1+n);//prev_permutation
 #define fo(a,b,c) for(register int a=b;a<=c;++a)
 #define fr(a,b,c) for(register int a=b;a>=c;--a)
 #define mem(a,b) memset(a,b,sizeof(a))
 #define pr printf
 #define sc scanf
 #define ls rt<<1
 #define rs rt<<1|1
 typedef long long ll;
 void swapp(int &a,int &b);
 double fabss(double a);
 int maxx(int a,int b);
 int minn(int a,int b);
 int Del_bit_1(int n);
 int lowbit(int n);
 int abss(int a);
 //const long long INF=(1LL<<60);
 const double E=2.718281828;
 const double PI=acos(-1.0);
 const int inf=(<<);
 const double ESP=1e-;
 const int mod=(int)1e9+;
 const int N=(int)1e6+;
 
 double dp[][][];
 
 int main()
 {
 //    freopen("C:\\Users\\13606\\Desktop\\草稿.txt","r",stdin);
     int T;
     sc("%d",&T);
     while(T--)
     {
         int n,m;
         sc("%d%d",&n,&m);
         dp[][][]=1.0;
         for(int k=;k<=n*m;++k)
         {
             for(int i=;i<=n;++i)
             {
                 for(int j=;j<=m;++j)
                 {
                      dp[i][j][k]=dp[i-][j][k-]*(n+-i)*j/(n*m+-k)
                                 +dp[i][j-][k-]*(m+-j)*i/(n*m+-k)
                                  +dp[i-][j-][k-]*(n+-i)*(m+-j)/(n*m+-k);
                     if(i<n||j<m)
                         dp[i][j][k]+=dp[i][j][k-]*(i*j+-k)/(n*m+-k);
                 }
             }
         }
         double ans=;
         for(int i=;i<=n*m;++i)
             ans+=i*dp[n][m][i];
         pr("%.10lf\n",ans);
     }
     return ;
 }
 
 /**************************************************************************************/
 
 int maxx(int a,int b)
 {
     return a>b?a:b;
 }
 
 void swapp(int &a,int &b)
 {
     a^=b^=a^=b;
 }
 
 int lowbit(int n)
 {
     return n&(-n);
 }
 
 int Del_bit_1(int n)
 {
     return n&(n-);
 }
 
 int abss(int a)
 {
     return a>?a:-a;
 }
 
 double fabss(double a)
 {
     return a>?a:-a;
 }
 
 int minn(int a,int b)
 {
     return a<b?a:b;
 }