K：哈弗曼树

相关介绍:

 树形结构除了应用于查找和排序等操作时能调高效率，它在信息通讯领域也有着广泛的应用。哈弗曼(Huffman)树就是一种在编码技术方面得到广泛应用的二叉树，它同时也是一种最优二叉树。

哈弗曼树相关的的基本概念:

 为了给出哈弗曼树的定义，从以下几个基本概念出发并进行描述。

1. 节点间的路径和节点的路径长度：所谓节点间的路径是指一个节点到另一个节点所经历的节点和分支序列。节点的路径长度是指从根节点到该节点间的路径上的分支数目。

2. 节点的权和节点的带权路径：在实际应用中，人们往往会给树中的每一个节点赋予一个具有某种实际意义的数值，这个数值称为节点的权值。节点的带权路径长度就是该节点的路径长度与该节点的权值的乘积。

3. 树的带权路径长度：树的带权路径长度就是树中所有叶节点的带权路径长度之和，通常记为：\(WPL=\sum_{i=1}^{n}W_{i} \times L_{i}\)其中，n为叶节点的个数，\(W_{i}\)为第i个叶节点的权值，\(L_{i}\)为第i个叶节点的路径长度

4. 最优二叉树：给定n个权值并作为n个叶节点按一定规则构造一棵二叉树，使得其带权路径长度达到最小值，则这棵二叉树被称为最优二叉树。下图展示了具有不同带权路径长度的二叉树，其中，第二棵树为最优二叉树

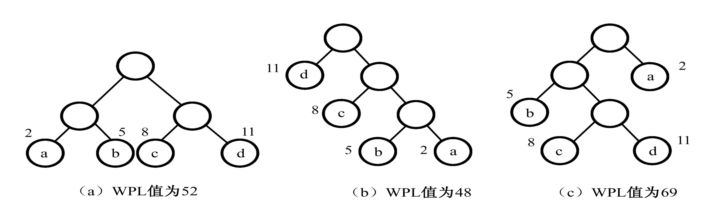
哈弗曼树和哈弗曼编码的构造方法

 哈弗曼树的构造步骤如下所示:

 假设n个叶节点的权值分别为{w1,w2,...,wn},则

1. 由已知给定的n个权值{w1,w2,w3,...,wn},构造一个由n棵二叉树所构成的森林F={T1，,T2,T3,...,Tn}，其中每一棵二叉树只有一个根节点，并且根节点的权值分别为w1，w2，....，wn

2. 在二叉树森林F中选取根节点的权值最小和次小的两棵二叉树，分别把它们作为左子树和右子树去构造一棵新二叉树，新二叉树的根节点权值为其左、右子树根节点的权值之和

3. 作为新二叉树的左右子树的两棵二叉树从森林F中删除。将新产生的二叉树加入到森林F中

4. 重复步骤2和步骤3，直到森林中只剩下一棵二叉树为止，则这棵二叉树就是所构成的哈弗曼树

下图展示了哈弗曼树的构造过程:

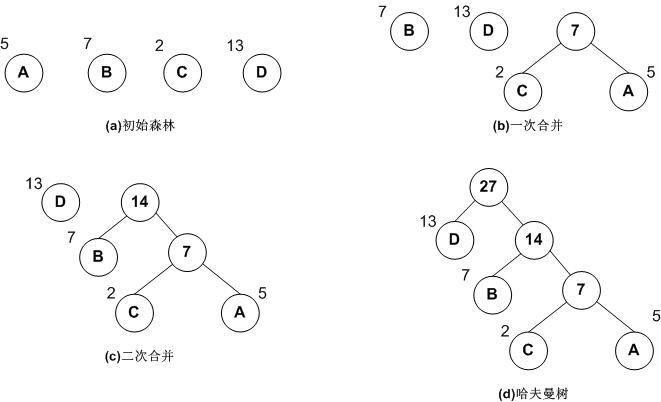
哈弗曼树构造过程的代码实现

 以下其代码演示了哈弗曼树的构造实现其中，测试代码所用的图如下所示:

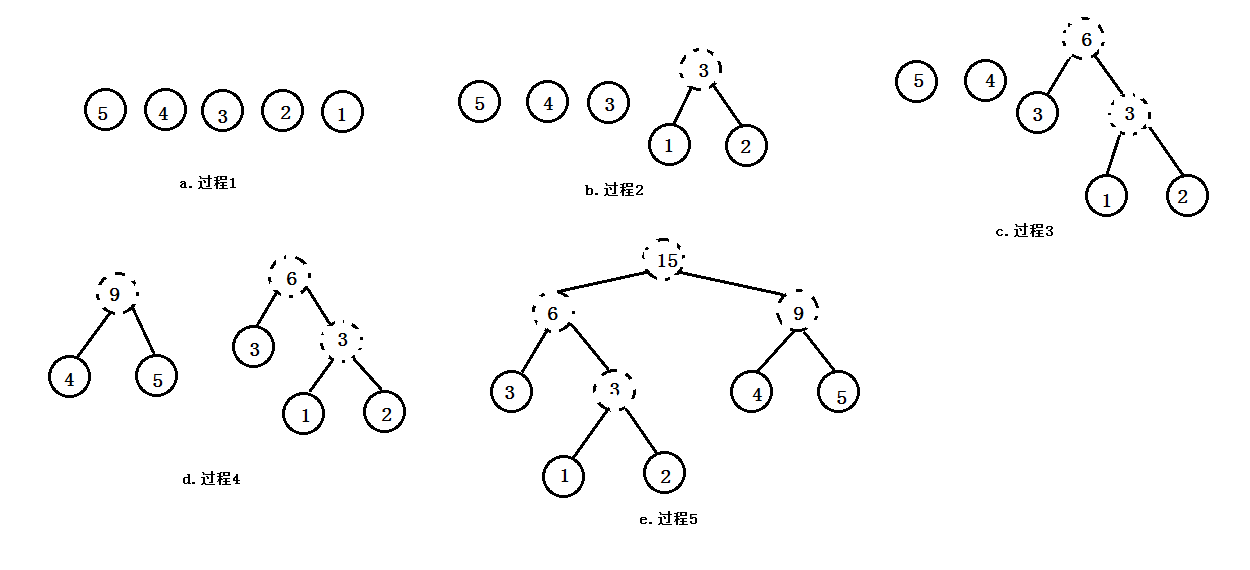
相关代码:

package all_in_tree;

import java.util.Comparator;
import java.util.LinkedList;
import java.util.PriorityQueue;
import java.util.Queue;

/**
 * 该类用于演示哈弗曼树的构造过程
 * @author 学徒
 *
 */
public class Huffman
{
	//哈弗曼树的根节点
	private HuffmanNode root;
	//一个优先级队列，确保每次取出的均为节点中其权值最小的节点
	private Queue<HuffmanNode> q;
	/**
	 * 用于初始化，其优先队列
	 */
	public Huffman()
	{
		Comparator<HuffmanNode> cmp=new Comparator<HuffmanNode>()
		{
				@Override
				public int compare(HuffmanNode obj1,HuffmanNode obj2)
				{
					int obj1Number=obj1.weight;
					int obj2Number=obj2.weight;
					if(obj1Number>obj2Number)
						return 1;
					else if(obj1Number<obj2Number)
						return -1;
					else
						return 0;
				}
		};
		q=new PriorityQueue<HuffmanNode>(11,cmp);
	}
	/**
	 * 用于添加节点到优先队列中，进行哈弗曼树的构造
	 * @param node
	 */
	public void addHuffmanNode(HuffmanNode node)
	{
		q.add(node);
	}
	/**
	 * 用于构造哈弗曼树
	 */
	public HuffmanNode createHuffmanTree()
	{
		while(!q.isEmpty()&&q.size()>=2)
		{
			HuffmanNode node1=q.poll();
			HuffmanNode node2=q.poll();
			HuffmanNode newNode=new HuffmanNode();
			newNode.weight=node1.weight+node2.weight;
			newNode.left=node1;
			newNode.right=node2;
			q.add(newNode);
		}
		if(!q.isEmpty())
			this.root=q.poll();
		return this.root;
	}
	/**
	 * 用于测试相关的代码
	 */
	public static void main(String[] args)
	{
		Huffman tree=new Huffman();
		for(int i=0;i<5;i++)
		{
			tree.addHuffmanNode(new HuffmanNode((char)('A'+i),i+1));
		}
		HuffmanNode root=tree.createHuffmanTree();
		System.out.println("其最高顶点的权值"+root.weight);
		//对该哈弗曼树进行层次遍历
		Queue<HuffmanNode> q=new LinkedList<HuffmanNode>();
		q.add(root);
		while(!q.isEmpty())
		{
			HuffmanNode node=q.poll();
			System.out.print(node.weight+"\t");
			if(node.left!=null)
				q.add(node.left);
			if(node.right!=null)
				q.add(node.right);
		}
	}
}
/**
 * 用于创建哈弗曼树的节点类的描述
 * @author 学徒
 *
 */
class HuffmanNode
{
	//用于存放相关的数据
	Object data;
	//用于记录该节点的权
	int weight;
	//该节点的左孩子
	HuffmanNode left;
	//该节点的右孩子
	HuffmanNode right;
	public HuffmanNode()
	{
	}
	public HuffmanNode(Object data,int weight)
	{
		this.data=data;
		this.weight=weight;
	}
}

运行结果:

其最高顶点的权值15
15	6	9	3	3	4	5	1	2

回到目录|·(工)·）