树和二叉树的存储结构的实现(C/C++实现)

存档：

 #include <iostream.h>
 #include <stdio.h>
 #include <stdlib.h>
 #define max 20
 typedef char elemtype;
 #include "tree.h"
 void main()
 {
     btree t,p;
     char x;
     int i=,num=;
     cout<<"(1)初始化二叉树initbt(t):"<<endl;
     initbt(t);
     cout<<"(2)输入先序遍历序列,创建二叉树(空树以#表示)createbt(t):"<<endl;
     createbt(t);
     cout<<"判断二叉树是否为空树emptybt(t):";
     i=emptybt(t);
     if(i==)
         cout<<"二叉树为空树!"<<endl;
     else
         cout<<"二叉树非空!"<<endl;
     cout<<"(4)输出二叉树的括号描述displaybt(t):";
     displaybt(t);
     cout<<endl;
     cout<<"(5)二叉树的深度depthbt(t)为:"<<depthbt(t)<<endl;
     cout<<"(6)二叉树的叶子结点的个数leafcount(t,num)为:";
     leafcount(t,num);
     cout<<num<<endl;
     cout<<"(7)二叉树的结点总个数nodecount(t)为:"<<nodecount(t)<<endl;
     cout<<"(8)先序遍历preorder(t)的结果为:";
     preorder(t);
     cout<<endl;
     cout<<"(9)中序遍历inorder(t)的结果为:";
     inorder(t);
     cout<<endl;
     cout<<"(10)后序遍历postorder(t)的结果为:";
     postorder(t);
     cout<<endl;
     cout<<"(11)层次遍历levelorder(t)的结果为:";
     levelorder(t);
     cout<<endl;
     fflush(stdin);//清空缓存
     cout<<"(12)输入一个字符,并在树中查找该字符是否存在findnode(t,x):";
     cin>>x;
     if(findnode(t,x))
         cout<<"字符存在!";
     else
         cout<<"字符不存在!";
     cout<<endl;
     cout<<"(13)字符"<<x<<"对应结点findnode1(t,x)的孩子为:"<<endl;
     p=findnode1(t,x);
     if(p!=NULL)
     {
         if(p->lchild!=NULL)
             cout<<x<<"左孩子为:"<<p->lchild->data<<" ";
         else
             cout<<x<<"无左孩子"<<" ";
         if(p->rchild!=NULL)
             cout<<x<<"右孩子为:"<<p->rchild->data<<endl;
         else
             cout<<x<<"无右孩子"<<endl;
     }
     else
         cout<<x<<"不存在"<<endl;
     cout<<"(14)清空clearbt(t)的结果为:";
     clearbt(t);
     if(emptybt(t))
         cout<<"二叉树为空树!"<<endl;
     else
         cout<<"二叉树非空!"<<endl;
     cout<<"(15)按照二叉树的括号描述createbt1(t,str)创建二叉树A(B(D,E),C(,F))";
     createbt1(t,"A(B(D,E),C(,F))");
     cout<<endl;
     cout<<"输出二叉树的括号描述displaybt(t):";
     displaybt(t);
     cout<<endl;
     cout<<"先序遍历preorder(t)的结果为:";
     preorder(t);
     cout<<endl;
     cout<<"中序遍历inorder(t)的结果为:";
     inorder(t);
     cout<<endl;
     clearbt(t);
     system("pause");
 }

 struct node
 {
     elemtype data;//数据元素
     struct node *lchild;//指向左孩子
     struct node *rchild;//指向右孩子
 };
 typedef struct node btnode;//定义结构体的别名btnode
 typedef struct node *btree;//定义结构体指针的别名btree
 void initbt(btree &t)//初始化函数,构造一棵空树
 {
     t=NULL;
 }
 void createbt(btree &t)//先序遍历序列创建二叉树
 {
     elemtype ch;
     cin>>ch;
     if(ch=='#')
         t=NULL;//#表示空树,递归终止
     else
     {
         t=new btnode;//创建新结点
         if(t==NULL)//如果创建结点失败,就退出
             exit(-);
         t->data=ch;//生成根结点
         createbt(t->lchild);//构造左子树
         createbt(t->rchild);//构造右子树
     }
 }
 int emptybt(btree t)//判断树是否为空树
 {
     if(t==NULL)
         return ;//空树返回1
     else
         return ;//非空树返回0
 }
 int depthbt(btree t)//求二叉树t的深度
 {
     if(t==NULL)
         return ;//空树深度为0
     else
     {
         int depthl=depthbt(t->lchild);//求左子树的高度为depthl
         int depthr=depthbt(t->rchild);//求右子树的高度为depthr
         return +(depthl>depthr?depthl:depthr);//子树深度最大的+1
     }
 }
 int findnode(btree t,elemtype x)//仿照先序遍历,查找data域为x的结点是否存在
 {
     int i;
     if(t==NULL)
         return ;//t为空树,无结点,不存在x,返回0
     else if(t->data==x)//t结点恰好是x对应结点,返回1
         return ;
     else
     {
         i=findnode(t->lchild,x);//在左子树中去查找x
         if(i!=)//如果找到了就返回
             return i;
         else
             return findnode(t->rchild,x);//没找到就去右子树中查找x
     }
 }
 btree findnode1(btree t,elemtype x)//仿照先序遍历,查找data域为x的结点,返回结点指针
 {
     btree p;
     if(t==NULL)
         return NULL;//t为空树,不存在x,返回NULL
     else if(t->data==x)//t结点恰好是x对应结点,返回t
         return t;
     else
     {
         p=findnode1(t->lchild,x);//在左子树中去查找x
         if(p!=NULL)//如果找到了就返回
             return p;
         else
             return findnode1(t->rchild,x);//没找到就去右子树中查找x
     }
 }
 void preorder(btree t)//先序遍历的递归算法
 {
     if(t!=NULL)
     {
         cout<<t->data<<' ';//访问根结点
         preorder(t->lchild);//递归访问左子树
         preorder(t->rchild);//递归访问右子树
     }
 }
 void inorder(btree t)//中序遍历的递归算法
 {
     if(t!=NULL)
     {
         inorder(t->lchild);//递归访问左子树
         cout<<t->data<<' ';//访问根结点
         inorder(t->rchild);//递归访问右子树
     }
 }
 void postorder(btree t)//后序遍历的递归算法
 {
     if(t!=NULL)
     {
         postorder(t->lchild);//递归访问左子树
         postorder(t->rchild);//递归访问右子树
         cout<<t->data<<' ';//访问根结点
     }
 }
 void clearbt(btree &t)//仿照后序遍历的递归算法
 {
     if(t!=NULL)
     {
         clearbt(t->lchild);//先清空左子树
         clearbt(t->rchild);//后清空右子树
         delete t;//删除根结点
         t=NULL;
     }
 }
 void levelorder(btree t)//借助循环队列的原理,实现层次遍历
 {
     btree queue[max];//定义循环队列
     int front,rear;//定义队首和队尾指针
     front=rear=;//置队列为空队列
     if(t!=NULL)
         cout<<t->data<<' ';//先访问再入队列
     queue[rear]=t;
     rear++;//结点指针入队列
     while(rear!=front)//队列不为空,继续循环
     {
         t=queue[front];//队头出队列
         front=(front+)%max;
         if(t->lchild!=NULL)//输出左孩子,并入队列
         {
             cout<<t->lchild->data<<' ';
             queue[rear]=t->lchild;
             rear=(rear+)%max;
         }
         if(t->rchild!=NULL)//输出右孩子,并入队列
         {
             cout<<t->rchild->data<<' ';
             queue[rear]=t->rchild;
             rear=(rear+)%max;
         }
     }
 }
 int nodecount(btree t)//求二叉树t的结点个数
 {
     int num1,num2;
     if(t==NULL)
         return ;//空树结点个数为0
     else
     {
         num1=nodecount(t->lchild);//左子树结点个数
         num2=nodecount(t->rchild);//右子树结点个数
         return (num1+num2+);//左子树+右子树+1
     }
 }
 void leafcount(btree t,int &count)//求二叉树t的叶子结点的个数
 {
     if(t!=NULL)
     {
         if(t->lchild==NULL&&t->rchild==NULL)
             count++;//叶子结点计算
         leafcount(t->lchild,count);//左子树叶子个数
         leafcount(t->rchild,count);//右子树叶子个数
     }
 }
 void displaybt(btree t)//以广义表法输出二叉树
 {
     if(t!=NULL)
     {
         cout<<t->data;
         if(t->lchild!=NULL||t->rchild!=NULL)
         {
             cout<<'(';
             displaybt(t->lchild);
             if(t->rchild!=NULL)
                 cout<<',';
             displaybt(t->rchild);
             cout<<')';
         }
     }
 }
 void createbt1(btree &t,char *str)//由广义表str串创建二叉链
 {
     btnode *st[max];
     btnode *p=NULL;
     int top=-,k,j=;
     char ch;
     t=NULL;//建立的二叉树初始化为空
     ch=str[j];
     while(ch!='\0')//str未扫描完时循环
     {
         switch(ch)
         {
             case '(':top++;st[top]=p;k=;break;//为左结点
             case ')':top--;break;
             case ',':k=;break;//为右结点
             default:p=new btnode;
             p->data=ch;
             p->lchild=p->rchild=NULL;
             if(t==NULL)//p指向二叉树的根结点
                 t=p;
             else//已建立二叉树根结点
             {
                 switch(k)
                 {
                     case :st[top]->lchild=p;break;
                     case :st[top]->rchild=p;break;
                 }
             }
         }
         j++;
         ch=str[j];
     }
 }

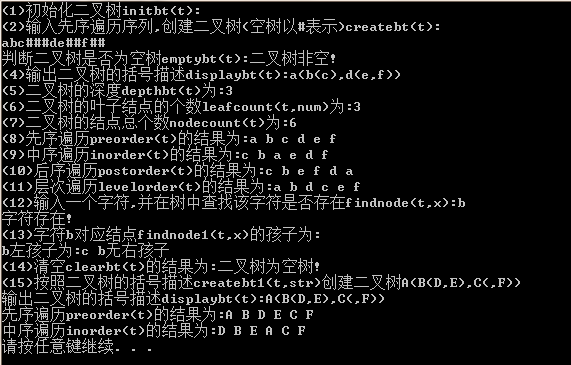
运行结果如下：