Gym 100952J&&2015 HIAST Collegiate Programming Contest J. Polygons Intersection【计算几何求解两个凸多边形的相交面积板子题】

J. Polygons Intersection

time limit per test：2 seconds

memory limit per test：64 megabytes

input：standard input

output：standard output

We will not waste your time, it is a straightforward problem. Given multiple polygons, calculate the area of their intersection. For simplicity, there will be exactly 2 polygons both of them are convex, given in the counterclockwise order and have non-zero areas. Furthermore, in one polygon a vertex won't be on the sides of the other one. The figure below demonstrates the first test case.

Input

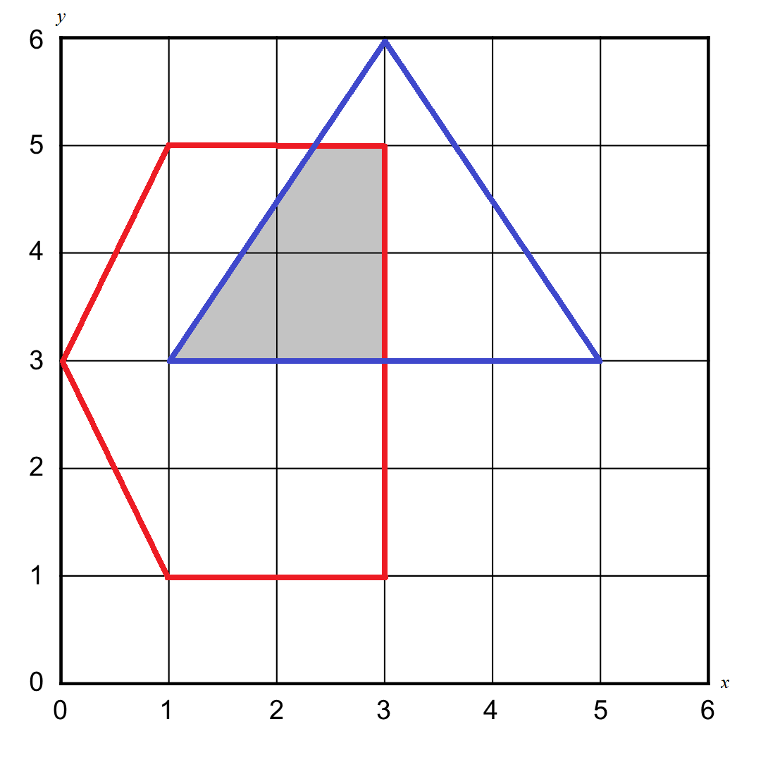
The first line of the input will be a single integer T, the number of test cases (1  ≤  T  ≤  20). each test case contains two integers (3  ≤  N, M  ≤  40) Then a line contains N pairs of integers x_i, y_i (-1000  ≤  x_i, y_i  ≤  1000) coordinates of the ith vertex of polygon A, followed by a line contains M pairs of integers x_j, y_j (-1000  ≤  x_j, y_j  ≤  1000) coordinates of the jth vertex of polygon B. The coordinates are separated by a single space.

Output

For each test case, print on a single line, a single number representing the area of intersection, rounded to four decimal places.

Examples

Input

2
5 3
0 3 1 1 3 1 3 5 1 5
1 3 5 3 3 6
3 3
-1 -1 -2 -1 -1 -2
1 1 2 1 1 2

Output

2.6667
0.0000

题目链接：http://codeforces.com/gym/100952/problem/J

题意：给2个凸多边形，求相交面积

思路：板子题，学习一下！

下面给出AC代码：

 #include "iostream"
 #include "string.h"
 #include "stack"
 #include "queue"
 #include "string"
 #include "vector"
 #include "set"
 #include "map"
 #include "algorithm"
 #include "stdio.h"
 #include "math.h"
 #define ll long long
 #define bug(x) cout<<x<<" "<<"UUUUU"<<endl;
 #define mem(a) memset(a,0,sizeof(a))
 #define mp(x,y) make_pair(x,y)
 using namespace std;
 const long long INF = 1e18+1LL;
 const int inf = 1e9+1e8;
 const int N=1e5+;
 #define maxn 510
 const double eps=1E-;
 int sig(double d){
     return(d>eps)-(d<-eps);
 }
 struct Point{
     double x,y; Point(){}
     Point(double x,double y):x(x),y(y){}
     bool operator==(const Point&p)const{
         return sig(x-p.x)==&&sig(y-p.y)==;
     }
 };
 double cross(Point o,Point a,Point b){
     return(a.x-o.x)*(b.y-o.y)-(b.x-o.x)*(a.y-o.y);
 }
 double area(Point* ps,int n){
     ps[n]=ps[];
     double res=;
     for(int i=;i<n;i++){
         res+=ps[i].x*ps[i+].y-ps[i].y*ps[i+].x;
     }
     return res/2.0;
 }
 int lineCross(Point a,Point b,Point c,Point d,Point&p){
     double s1,s2;
     s1=cross(a,b,c);
     s2=cross(a,b,d);
     if(sig(s1)==&&sig(s2)==) return ;
     if(sig(s2-s1)==) return ;
     p.x=(c.x*s2-d.x*s1)/(s2-s1);
     p.y=(c.y*s2-d.y*s1)/(s2-s1);
     return ;
 }
 //多边形切割
 //用直线ab切割多边形p，切割后的在向量(a,b)的左侧，并原地保存切割结果
 //如果退化为一个点，也会返回去,此时n为1
 void polygon_cut(Point*p,int&n,Point a,Point b){
     static Point pp[maxn];
     int m=;p[n]=p[];
     for(int i=;i<n;i++){
         if(sig(cross(a,b,p[i]))>) pp[m++]=p[i];
         if(sig(cross(a,b,p[i]))!=sig(cross(a,b,p[i+])))
             lineCross(a,b,p[i],p[i+],pp[m++]);
     }
     n=;
     for(int i=;i<m;i++)
         if(!i||!(pp[i]==pp[i-]))
             p[n++]=pp[i];
     while(n>&&p[n-]==p[])n--;
 }
 //---------------华丽的分隔线-----------------//
 //返回三角形oab和三角形ocd的有向交面积,o是原点//
 double intersectArea(Point a,Point b,Point c,Point d){
     Point o(,);
     int s1=sig(cross(o,a,b));
     int s2=sig(cross(o,c,d));
     if(s1==||s2==)return 0.0;//退化，面积为0
     if(s1==-) swap(a,b);
     if(s2==-) swap(c,d);
     Point p[]={o,a,b};
     int n=;
     polygon_cut(p,n,o,c);
     polygon_cut(p,n,c,d);
     polygon_cut(p,n,d,o);
     double res=fabs(area(p,n));
     if(s1*s2==-) res=-res;return res;
 }
 //求两多边形的交面积
 double intersectArea(Point*ps1,int n1,Point*ps2,int n2){
     if(area(ps1,n1)<) reverse(ps1,ps1+n1);
     if(area(ps2,n2)<) reverse(ps2,ps2+n2);
     ps1[n1]=ps1[];
     ps2[n2]=ps2[];
     double res=;
     for(int i=;i<n1;i++){
         for(int j=;j<n2;j++){
             res+=intersectArea(ps1[i],ps1[i+],ps2[j],ps2[j+]);
         }
     }
     return res;//assumeresispositive!
 }
 //hdu-3060求两个任意简单多边形的并面积
 Point ps1[maxn],ps2[maxn];
 int n1,n2;
 int main(){
     int t;
     cin>>t;
     while(t--){
         scanf("%d%d",&n1,&n2);
         for(int i=;i<n1;i++)
             scanf("%lf%lf",&ps1[i].x,&ps1[i].y);
         for(int i=;i<n2;i++)
             scanf("%lf%lf",&ps2[i].x,&ps2[i].y);
         double ans=intersectArea(ps1,n1,ps2,n2);
         //ans=fabs(area(ps1,n1))+fabs(area(ps2,n2))-ans;//容斥
         printf("%.4f\n",ans);
     }
     return ;
 }