BinarySearchTree-二叉搜索树
一、二叉搜索树的定义及性质
二叉查找树（Binary Search Tree），也称有序二叉树（ordered binary tree）,排序二叉树（sorted binary tree），是指一棵空树或者具有下列性质的二叉树：
1. 每个节点都有一个作为搜索依据的关键码（ key） ， 所有节点的关键码互不相同。
2. 左子树上所有节点的关键码（ key） 都小于根节点的关键码（ key） 。
3. 右子树上所有节点的关键码（ key） 都大于根节点的关键码（ key） 。
4. 左右子树都是二叉搜索树。
在实现中，由它的性质可以初步简单的定义出节点信息，我们需要定义一个内部类BinarySearchTreeNode，它包含两个分别指向左右节点的Node->_left和Node->_right，一个保存键值信息的Key。
template <class K>
struct BinarySearchTreeNode
{
BinarySearchTreeNode<K>* _left; //指向左子树
BinarySearchTreeNode<K>* _right; //指向右子树
K _key; //关键码
BinarySearchTreeNode(const K& key)
:_left(NULL)
,_right(NULL)
,_key(key)
{}
};
如下图，这个是普通的二叉树，它具有普通二叉树的所有性质。
在此基础上，加上上面所述节点之间的大小关系，就是二叉查找树：
下面这个是二叉搜索树，可以很清晰的看出节点之间的大小关系：
而二叉搜索树里面真正有意义的是对其节点的增、删、查找等操作，下面我分别来介绍这几种算法原理。
二、算法操作
由内部节点构建二叉搜索树如下：
template<class K>
class BinarySearchTree
{
typedef BinarySearchTreeNode<K> Node;
public:
BinarySearchTree()
:_root(NULL)
{}
~BinarySearchTree()
{
_Delete(_root);
}
//非递归
bool Insert(const K& key) //插入
{
return _Insert(_root, key);
}
bool Remove(const K& key) //删除
{
return _Remove(_root, key);
}
const Node* Find(const K& key) //查找
{
return _Find(_root, key);
}
//递归
bool InsertR(const K& key)
{
return _InsertR(_root, key);
}
bool RemoveR(const K& key)
{
return _RemoveR(_root, key);
}
const Node* FindR(const K& key)
{
return _FindR(_root, key);
}
void Inorder() //遍历打印
{
_Inorder(_root);
cout << endl;
}
private:
void _Delete(Node*& root);
bool _Insert(Node* root, const K& key);
bool _Remove(Node* root, const K& key);
Node* _Find(Node* root, const K& key);
bool _InsertR(Node*& root, const K& key);
bool _RemoveR(Node* & root, const K& key);
const Node*_FindR(Node* root, const K& key);
void _Inorder(Node* root);
private:
Node* _root;
};
1.查找
查找操作和二分查找类似，从根节点开始，将root->_key和要找的节点的key比较，如果root->_key小于要找的节点的key，那么就在左子树 _root->_left节点中查找,如果root->_key大于要找的节点的key，则在右子树_root->_right节点中查找，如果_root->_key和要找的节点的key相等，直接返回此节点。
查找操作图示如下：
该方法实现有递归和非递归两种。
非递归算法程序如下：
const Node* Find(const K& key)
{
return _Find(_root, key);
}
Node* _Find(Node* root, const K& key)
{
while (root) {
if (root->_key > key) //向左查找
root = root->_left;
if (root->_key < key) //向右查找
root = root->_right;
else
return root; //找到节点
}
return NULL;
}
递归算法：
const Node* FindR(const K& key)
{
return _FindR(_root, key);
}
const Node*_FindR(Node* root, const K& key)
{
if (root == NULL)
return NULL;
if (root->_key > key)
return _FindR(root->_left, key); //向左递归查找
if (root->_key < key)
return _FindR(root->_right, key); //向右递归查找
else
return root; //找到该节点
}
2.插入
插入一个节点第一步与与查找类似，首先要找到应该插入节点的位置，因为插入节点后不能破坏二叉搜索树的性质。首先判断如果树为空，则直接动态开辟节点并初始化为key插入即可，插入的节点即为根节点。然后再向下查找应该插入节点的位置，查找方法与上一个查找算法类似，不同的是在查找的过程中要将应该插入的位置的父节点记录下来。找到该位置后，将parent->_key与插入的key进行比较，判断应该插入到父节点的左子树还是右子树。如果parent->_key小于要插入节点的key，那么就插入为父节点的右子树parent->_right = new Node(key); //插入右子树；如果parent->_key大于要插入节点的key，那么就插入为父节点的左子树parent->_left = new Node(key); //插入左子树。
插入操作图示如下：
同样，插入操作的实现也有递归和非递归两种方法。
非递归法实现如下：
bool Insert(const K& key)
{
return _Insert(_root, key);
}
bool Insert(Node*& root， const K& key) {
if (root == NULL){ //当树为空时，直接插入
root = new Node(key);
return true;
}
Node* cur = root;
Node* parent = cur;
while (cur) { //找到要插入的位置
if (cur->_key > key) {
parent = cur;
cur = cur->_left;
}
else if (cur->_key < key) {
parent = cur;
cur = cur->_right;
}
else
return false;
}
if (parent->_key < key) //找到插入位置的父节点，判断应该是父节点的左子树还是右子树右
parent->_right = new Node(key); //插入右子树
else
parent->_left = new Node(key); //插入左子树
return true;
}
递归法实现如下：
bool InsertR(const K& key)
{
return _InsertR(_root, key);
}
bool _InsertR(Node*& root, const K& key) //注意：这里参数传递方法是传引用
{
if (root == NULL){
root = new Node(key);
return true;
}
if (root->_key > key)
return _InsertR(root->_left, key);
if (root->_key < key)
return _InsertR(root->_right, key);
else
return false;
}
3.删除
删除元素操作在二叉树的操作中应该是比较复杂的。但是只要一步一步分析的话其实也是比较容易实现的。首先判断该树是否为空，为空的话直接返回删除失败；该是不为空时，第一步是找到需要删除的节点，方法与前面的查找算法类似，不同的是也需要将删除的节点的父节点记录下来，以判断该节点删除以后需要调整父节点的哪一个子树。找到该节点后，复杂的地方才刚开始。
（1）当要删除的节点的左子树为空时，判断是否为该节点是否为根节点，若是，则直接删除，其右子树的根节点成为新的根节点；若不是则再次判断该节点在其父节点的哪个子树上。若该节点在其父节点的左子树上，则将该节点的右子树连到该节点的父节点的左子树上，然后将该节点删除；若该节点在其父节点的右子树上，则将该节点的右子树连到该节点的父节点的右子树上，然后将该节点删除。
（2）当要删除的节点的右子树为空时，判断是否为该节点是否为根节点，若是，则直接删除，其左子树的根节点成为新的根节点；若不是则再次判断该节点在其父节点的哪个子树上。若该节点在其父节点的左子树上，则将该节点的左子树连到该节点的父节点的左子树上，然后将该节点删除；若该节点在其父节点的右子树上，则将该节点的左子树连到该节点的父节点的右子树上，然后将该节点删除。（类似于（1））。
（3）当要删除的节点的左右子树都不为为空时，首先查找该节点的右子树的最小节点，即找该节点的右子树的最左节点，让这个最小节点代替该节点的位置，然后将此最小节点删除，这样调整之后才能使此树依然为搜索二叉树，另外在查找最左节点时应将它的父节点记录下来（原理同（1）和（2））。找到该节点的右子树的最左节点后，将最左节点的值赋给要删除的节点，作为新的该节点，其原值被覆盖，后面再删除的就是找到的最左节点。删除之前判断若此最左节点在其父节点的左子树上，则将该节点的右子树连到该节点的父节点的左子树上，然后将该节点删除；若该节点在其父节点的右子树上（即右子树最左节点为右子树的根节点），则将该节点的右子树连到该节点的父节点的右子树上，然后将该节点删除。（还有另一种方法，就是找到该节点的右子树的最大节点，即最右节点，与该节点替换后再删除，原理相同，此处不在赘述）。
此原理叙述起来较复杂，下面请看图示情况分类：
当删除的节点只有1个子节点时，在左边和在右边原理类似：
当删除的节点有2个子节点时：
用具体的二叉查找树举例如下：
非递归法代码如下：
bool Remove(const K& key) {
if (_root == NULL)
return false;
Node* del = _root;
Node* parent = del;
while (del) {
if (del->_key < key) { //向右搜索
parent = del;
del = del->_right;
}
if (del->_key > key) { //向左搜索
parent = del;
del = del->_left;
}
if (del->_key == key) { //要删除的节点找到
Node* cur = del;
if (cur->_left == NULL) { //当此节点左子树为空
if (_root->_key == key) //删除根节点
_root = _root->_right;
else{
if(parent->_left == cur)
parent->_left = cur->_right; //当找到的节点在其父节点的左子树上
else
parent->_right = cur->_right; //当找到的节点在其父节点的右子树上
}
}
else if (cur->_right == NULL) { //当此节点右子树为空
if (_root->_key == key)
_root = _root->_left;
else {
if (parent->_left == cur)
parent->_left = cur->_left;
else
parent->_right = cur->_left;
}
}
else{ //左右子树都不为空
cur = cur->_right;
while (cur->_left) { //找右子树的最左节点
parent = cur;
cur = cur->_left;
}
del->_key = cur->_key; //将最左节点的值给要删除的节点，作为新的该节点，其原值被覆盖
del = cur; //后面删除的就是找到的最左节点
if (parent->_left == cur) //此时的cur是最左节点
parent->_left = cur->_right;
else
parent->_right = cur->_right; //右子树最左节点为右子树的根节点
}
delete del;
del = NULL;
return true;
}
}
return false;
}
递归法删除节点代码如下：
bool RemoveR(const K& key)
{
return _RemoveR(_root, key);
}
bool _RemoveR(Node* & root, const K& key) //注意此处传引用
{
if (root == NULL)
return false;
if (root->_key > key)
return _RemoveR(root->_left, key); //向左递归搜索
if (root->_key < key)
return _RemoveR(root->_right, key); //向右递归搜索
else{ //要删除的节点找到
Node* del = root;
if (root->_left == NULL)
root = root->_right;
if (root->_right == NULL)
root = root->_left;
else{
Node* cur = root;
Node* parent = cur;
cur = cur->_right;
while (cur->_left) {
parent = cur;
cur = cur->_left;
}
del->_key = cur->_key;
del = cur;
if (parent->_left = cur)
parent->_left = cur->_right;
else
parent->_right = cur->_right;
}
delete del;
del = NULL;
return true;
}
}
三、算法分析与总结
二叉查找树的运行时间和树的形状有关，树的形状又和插入元素的顺序有关。在最好的情况下，节点完全平衡，从根节点到最底层叶子节点只有lgN个节点。在最差的情况下，根节点到最底层叶子节点会有N各节点。在一般情况下，树的形状和最好的情况接近。
在分析二叉查找树的时候，我们通常会假设插入的元素顺序是随机的。对于N个不同元素，随机插入的二叉查找树来说，其平均查找/插入的时间复杂度大约为2lnN。
前面有对二分查找时间复杂度的分析，对二叉查找树的理解可以类比于此。它和二分查找一样，插入和查找的时间复杂度均为lgN，但是在最坏的情况下仍然会有N的时间复杂度。原因在于插入和删除元素的时候，树没有保持平衡。我们追求的是在最坏的情况下仍然有较好的时间复杂度，这就是后面要讲的平衡查找树的内容了。
下面是二叉查找树的时间复杂度：
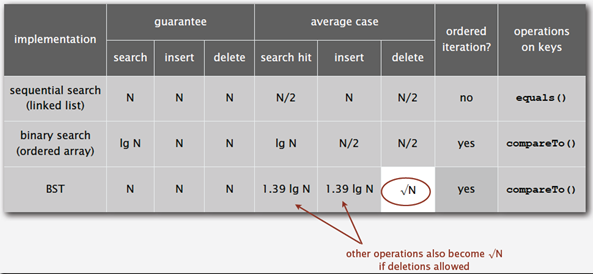
四、完整的二叉搜索树代码
#include<iostream>
using namespace std; template <class K>
struct BinarySearchTreeNode
{
BinarySearchTreeNode<K>* _left;
BinarySearchTreeNode<K>* _right;
K _key;
BinarySearchTreeNode(const K& key)
:_left(NULL)
,_right(NULL)
,_key(key)
{}
}; template<class K>
class BinarySearchTree
{
typedef BinarySearchTreeNode<K> Node;
public:
BinarySearchTree()
:_root(NULL)
{}
~BinarySearchTree()
{
_Delete(_root);
}
//非递归
bool Insert(const K& key)
{
return _Insert(_root, key);
}
bool Remove(const K& key)
{
return _Remove(_root, key);
}
const Node* Find(const K& key)
{
return _Find(_root, key);
}
//递归
bool InsertR(const K& key)
{
return _InsertR(_root, key);
}
bool RemoveR(const K& key)
{
return _RemoveR(_root, key);
}
const Node* FindR(const K& key)
{
return _FindR(_root, key);
}
void Inorder()
{
_Inorder(_root);
cout << endl;
}
private:
void _Delete(Node*& root)
{
if (root)
{
_Delete(root->_left);
_Delete(root->_right);
delete root;
root = NULL;
}
return;
}
bool Insert(const K& key) {
if (_root == NULL){ //当树为空时，直接插入
_root = new Node(key);
return true;
}
Node* cur = _root;
Node* parent = cur;
while (cur) { //找到要插入的位置
if (cur->_key > key) {
parent = cur;
cur = cur->_left;
}
else if (cur->_key < key) {
parent = cur;
cur = cur->_right;
}
else
return false;
}
if (parent->_key < key) //找到插入位置的父节点，判断应该是父节点的左子树还是右子树右
parent->_right = new Node(key); //插入右子树
else
parent->_left = new Node(key); //插入左子树
return true;
} bool Remove(const K& key) {
if (_root == NULL)
return false;
Node* del = _root;
Node* parent = del;
while (del) {
if (del->_key < key) { //向右搜索
parent = del;
del = del->_right;
}
if (del->_key > key) { //向左搜索
parent = del;
del = del->_left;
}
if (del->_key == key) { //要删除的节点找到
Node* cur = del;
if (cur->_left == NULL) { //当此节点左子树为空
if (_root->_key == key) //删除根节点
_root = _root->_right;
else{
if(parent->_left == cur)
parent->_left = cur->_right; //当找到的节点在其父节点的左子树上
else
parent->_right = cur->_right; //当找到的节点在其父节点的右子树上
}
}
else if (cur->_right == NULL) { //当此节点右子树为空
if (_root->_key == key)
_root = _root->_left;
else {
if (parent->_left == cur)
parent->_left = cur->_left;
else
parent->_right = cur->_left;
}
}
else{ //左右子树都不为空
cur = cur->_right;
while (cur->_left) { //找右子树的最左节点
parent = cur;
cur = cur->_left;
}
del->_key = cur->_key; //将最左节点的值给要删除的节点，作为新的该节点，其原值被覆盖
del = cur; //后面删除的就是找到的最左节点
if (parent->_left == cur) //此时的cur是最左节点
parent->_left = cur->_right;
else
parent->_right = cur->_right; //右子树最左节点为右子树的根节点
}
delete del;
del = NULL;
return true;
}
}
return false;
}
Node* _Find(Node* root, const K& key)
{
while (root) {
if (root->_key > key) //向左查找
root = root->_left;
if (root->_key < key) //向右查找
root = root->_right;
else
return root; //找到节点
}
return NULL;
} bool _InsertR(Node*& root, const K& key)
{
if (root == NULL){
root = new Node(key);
return true;
}
if (root->_key > key)
return _InsertR(root->_left, key);
if (root->_key < key)
return _InsertR(root->_right, key);
else
return false;
}
bool _RemoveR(Node* & root, const K& key)
{
if (root == NULL)
return false;
if (root->_key > key)
return _RemoveR(root->_left, key); //向左递归搜索
if (root->_key < key)
return _RemoveR(root->_right, key); //向右递归搜索
else{ //要删除的节点找到
Node* del = root;
if (root->_left == NULL)
root = root->_right;
if (root->_right == NULL)
root = root->_left;
else{
Node* cur = root;
Node* parent = cur;
cur = cur->_right;
while (cur->_left) {
parent = cur;
cur = cur->_left;
}
del->_key = cur->_key;
del = cur;
if (parent->_left = cur)
parent->_left = cur->_right;
else
parent->_right = cur->_right;
}
delete del;
del = NULL;
return true;
} }
const Node*_FindR(Node* root, const K& key)
{
if (root == NULL)
return NULL;
if (root->_key > key)
return _FindR(root->_left, key);
if (root->_key < key)
return _FindR(root->_right, key);
else
return root;
}
void _Inorder(Node* root)
{
if (root)
{
_Inorder(root->_left);
cout << root->_key << " ";
_Inorder(root->_right);
}
}
private:
Node* _root;
};
//测试代码：
#include"SearchTree.h" void Test()
{
BinarySearchTree<int> tree;
tree.InsertR();
tree.InsertR();
tree.Insert();
tree.InsertR();
tree.Insert();
tree.InsertR();
tree.Insert();
tree.InsertR();
tree.Insert(); cout << tree.FindR() << endl;
cout << tree.FindR() << endl;
cout << tree.FindR() << endl;
cout << tree.FindR() << endl;
cout << tree.Find() << endl;
cout << tree.Find() << endl;
cout << tree.Find() << endl;
cout << tree.Find() << endl; tree.Inorder(); tree.RemoveR();
tree.RemoveR();
tree.RemoveR();
tree.Remove();
tree.Remove();
tree.Remove();
tree.Remove();
tree.Remove();
tree.Remove(); tree.~BinarySearchTree(); }
int main()
{
Test();
getchar();
return ;
}
部分测试代码的输出结果：
本文部分图示来自于：http://www.cnblogs.com/yangecnu/p/Introduce-Binary-Search-Tree.htm
BinarySearchTree-二叉搜索树的更多相关文章
- BinarySearchTree二叉搜索树的实现
/* 二叉搜索树(Binary Search Tree),(又:二叉查找树,二叉排序树)它或者是一棵空树,或者是具有下列性质的二叉树: 若它的左子树不空,则左子树上所有结点的值均小于它的根结点的值; ...
- 二叉搜索树详解（Java实现）
1.二叉搜索树定义 二叉搜索树,是指一棵空树或者具有下列性质的二叉树: 若任意节点的左子树不空,则左子树上所有节点的值均小于它的根节点的值: 若任意节点的右子树不空,则右子树上所有节点的值均大于它的根 ...
- BinarySearchTree（二叉搜索树）原理及C++代码实现
BST是一类用途极广的数据结构.它有如下性质:设x是二叉搜索树内的一个结点.如果y是x左子树中的一个结点,那么y.key<=x.key.如果y是x右子树中的一个结点,那么y.key>=x. ...
- javascript数据结构——写一个二叉搜索树
二叉搜索树就是左侧子节点值比根节点值小,右侧子节点值比根节点值大的二叉树. 照着书敲了一遍. function BinarySearchTree(){ var Node = function(key) ...
- Java二叉搜索树实现
树集合了数组(查找速度快)和链表(插入.删除速度快)的优点 二叉树是一种特殊的树,即:树中的每个节点最多只能有两个子节点 二叉搜索树是一种特殊的二叉树,即:节点的左子节点的值都小于这个节点的值,节点的 ...
- 数据结构-二叉树（应用篇）-之二叉搜索树 C和C++的实现
一.概念 二叉搜索树(Binary Sort Tree/Binary Search Tree...),是二叉树的一种特殊扩展.也是一种动态查找表. 在二叉搜索树中,左子树上所有节点的均小于根节点,右子 ...
- Java与算法之(13) - 二叉搜索树
查找是指在一批记录中找出满足指定条件的某一记录的过程,例如在数组{ 8, 4, 12, 2, 6, 10, 14, 1, 3, 5, 7, 9, 11, 13, 15 }中查找数字15,实现代码很简单 ...
- 二叉搜索树(Java实现)
二叉搜索树基本操作 求树中的结点个数 判断节点是否为空 向树中插入新结点key-value 树中是否存在key 返回树中key对应的value值 先序遍历 中序遍历 后续遍历 层序遍历 求树中key最 ...
- [数据结构]P2.1 二叉搜索树
二叉树就是每个节点最多有两个分叉的树.这里我们写一写一个典型的例子二叉搜索树,它存在的实际意义是什么呢? 在P1.1链表中,我们清楚了链表的优势是善于删除添加节点,但是其取值很慢:数组的优势是善于取值 ...
- 【IT笔试面试题整理】二叉搜索树转换为双向链表
[试题描述] 将二叉搜索树转换为双向链表 对于二叉搜索树,可以将其转换为双向链表,其中,节点的左子树指针在链表中指向前一个节点,右子树指针在链表中指向后一个节点. 思路一: 采用递归思想,对于二叉搜索 ...
随机推荐
- 使用AF_INET实现点对点的通信示例
作者:Younger Liu,本作品采用知识共享署名-非商业性使用-相同方式共享 3.0 未本地化版本许可协议进行许可. 1. 客户端(发送方) 操作流如下: (1) 使用AF_INET协议簇, ...
- 分针网—IT教育：作为PHP开发人员容易忽视的几个重点
无论是学习什么样的一个开发.ASP开发.java开发.当学习还不是很久的时候,一般都是不知道它们的精华是在哪里,而现在很多的php程序员也是不知道PHP的精华所在,为什么perl在当年在商界如此的出名 ...
- IOS(一) 基础控件的介绍以及使用
IOS的界面的制作,相对于Android来说 简洁了很多,虽然创建布局的方式都是两种(代码创建.布局文件) 但是Android中的xml布局文件在某些方面也属于代码创建,因为自己使用到得每一个属性 都 ...
- 记事本app TOP5（个人观点）
1.为知笔记 为知笔记定位于高效率工作笔记,主打工作笔记的移动应用,是目前国内唯一一款"工作笔记"的云笔记类产品.除了常用的笔记功能保存的网页.灵感笔记.重要文档.照片.便签等,为 ...
- Java学习笔记——设计模式之一.简单工厂
蜀道之难.难于上青天,侧身西望长咨嗟 --蜀道难 设计模式第一篇,简单工厂. 定义Operation类 package cn.no1.simplefactory; public abstract cl ...
- 【JAVAWEB学习笔记】16_session&cookie
会话技术Cookie&Session 学习目标 案例一.记录用户的上次访问时间---cookie 案例二.实现验证码的校验----session 一.会话技术简介 1．存储客户端的状态 由一个 ...
- 开涛spring3(3.3) - DI 之 3.3 更多DI的知识
3.3.1 延迟初始化Bean 延迟初始化也叫做惰性初始化,指不提前初始化Bean,而是只有在真正使用时才创建及初始化Bean. 配置方式很简单只需在<bean>标签上指定 “lazy- ...
- Python爬虫01——第一个小爬虫
Python小爬虫——贴吧图片的爬取 在对Python有了一定的基础学习后,进行贴吧图片抓取小程序的编写. 目标: 首先肯定要实现图片抓取这个基本功能 然后实现对用户所给的链接进行抓取 最后要有一定的 ...
- Tomcat 安装与配置
1. 将压缩文件“apache-tomcat-7.0.62.zip ”上传到linux系统目录:/home/下 2. 进入目录 cd /home/ 解压文件,执行如下命令:unzip apache-t ...
- 360你吃屎啊你，hao123,12345等等
请看到这个文章的小伙伴将文章看完,看看我的感受是有多深,谢谢了 现在浏览器已经是人们经常用的东西,相信都有时不时就差度娘的习惯吧 也就是说每个人都有自己喜欢的主页 可电脑有时候就是遭不住,360什么的 ...