BM算法详解

http://www-igm.univ-mlv.fr/~lecroq/string/node14.html

http://www.cs.utexas.edu/users/moore/publications/fstrpos.pdf

BM算法

　　后缀匹配，是指模式串的比较从右到左，模式串的移动也是从左到右的匹配过程，经典的BM算法其实是对后缀蛮力匹配算法的改进。为了实现更快移动模式串，BM算法定义了两个规则，好后缀规则和坏字符规则，如下图可以清晰的看出他们的含义。利用好后缀和坏字符可以大大加快模式串的移动距离，不是简单的++j，而是j+=max (shift(好后缀), shift(坏字符))

　　先来看如何根据坏字符来移动模式串，shift(坏字符)分为两种情况：

• 坏字符没出现在模式串中，这时可以把模式串移动到坏字符的下一个字符，继续比较，如下图：

• 坏字符出现在模式串中，这时可以把模式串第一个出现的坏字符和母串的坏字符对齐，当然，这样可能造成模式串倒退移动，如下图：

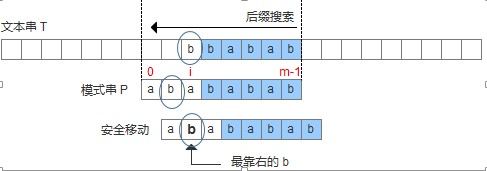
　　此处配的图是不准确的，因为显然加粗的那个b并不是”最 靠右的”b。而且也与下面给出的代码冲突！我看了论文，论文的意思是最右边的。当然了，尽管一时大意图配错了，论述还是没有问题的，我们可以把图改正一 下，把圈圈中的b改为字母f就好了。接下来的图就不再更改了，大家心里有数就好。
　　为了用代码来描述上述的两种情况，设计一个数组bmBc['k']，表示坏字符‘k’在模式串中出现的位置距离模式串末尾的最大长度，那么当遇到坏字符的时候，模式串可以移动距离为： shift(坏字符) = bmBc[T[i]]-（m-1-i)。如下图：

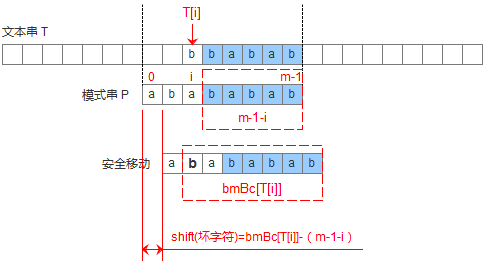
　　数组bmBc的创建非常简单，直接贴出代码如下：

 1 void preBmBc(char *x, int m, int bmBc[]) {
 2
 3    int i;
 4
 5    for (i = 0; i < ASIZE; ++i)
 6
 7       bmBc[i] = m;
 8
 9    for (i = 0; i <= m - 1; ++i)
10
11       bmBc[x[i]] = m - i - 1;
12
13 }

　　代码分析：

• ASIZE是指字符种类个数，为了方便起见，就直接把ASCII表中的256个字符全表示了，哈哈，这样就不会漏掉哪个字符了。
• 第一个for循环处理上述的第一种情况，这种情况比较容易理解就不多提了。第二个for循环，bmBc[x[i]]中x[i]表示模式串中的第i个字符。bmBc[x[i]] = m - i - 1;也就是计算x[i]这个字符到串尾部的距离。
• 为什么第二个for循环中，i从小到大的顺序计算呢？哈哈，技巧就在这儿了，原因在于就可以在同一字符多次出现的时候以最靠右的那个字符到尾部距离为最终的距离。当然了，如果没在模式串中出现的字符，其距离就是m了。

　　再来看如何根据好后缀规则移动模式串，shift（好后缀）分为三种情况：

• 模式串中有子串匹配上好后缀，此时移动模式串，让该子串和好后缀对齐即可，如果超过一个子串匹配上好后缀，则选择最靠左边的子串对齐。

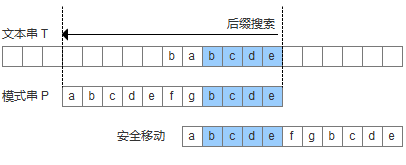
• 模式串中没有子串匹配上后后缀，此时需要寻找模式串的一个最长前缀，并让该前缀等于好后缀的后缀，寻找到该前缀后，让该前缀和好后缀对齐即可。

• 模式串中没有子串匹配上后后缀，并且在模式串中找不到最长前缀，让该前缀等于好后缀的后缀。此时，直接移动模式到好后缀的下一个字符。

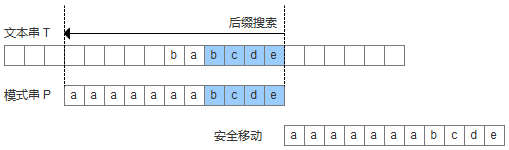
　　为了实现好后缀规则，需要定义一个数组suffix[]，其中suffix[i] = s 表示以i为边界，与模式串后缀匹配的最大长度，如下图所示，用公式可以描述：满足P[i-s, i] == P[m-s, m]的最大长度s。

　　构建suffix数组的代码如下：

 1 void suffixes(char *x, int m, int *suff)
 2  {
 3 　　suff[m-1]=m;
 4 　　for (i=m-2；i>=0；--i){
 5     q=i;
 6     while(q>=0&&x[q]==x[m-1-i+q])
 7         --q;
 8     suff[i]=i-q;
 9 }
10 }

　　·注解：这一部分代码乏善可陈，都是常规代码，这里就不多说了。

　　有了suffix数组，就可以定义bmGs[]数组，bmGs[i] 表示遇到好后缀时，模式串应该移动的距离，其中i表示好后缀前面一个字符的位置（也就是坏字符的位置），构建bmGs数组分为三种情况，分别对应上述的移动模式串的三种情况

• 模式串中有子串匹配上好后缀

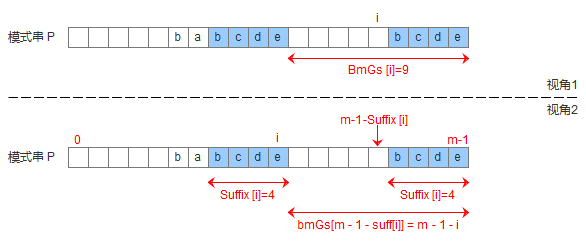
• 模式串中没有子串匹配上好后缀，但找到一个最大前缀

• 模式串中没有子串匹配上好后缀，但找不到一个最大前缀

　　构建bmGs数组的代码如下：

 1 void preBmGs(char *x, int m, int bmGs[]) {
 2    int i, j, suff[XSIZE];
 3    suffixes(x, m, suff);
 4    for (i = 0; i < m; ++i)
 5       bmGs[i] = m;
 6    j = 0;
 7    for (i = m - 1; i >= 0; --i)
 8       if (suff[i] == i + 1)
 9          for (; j < m - 1 - i; ++j)
10             if (bmGs[j] == m)
11                bmGs[j] = m - 1 - i;
12    for (i = 0; i <= m - 2; ++i)
13       bmGs[m - 1 - suff[i]] = m - 1 - i;
14 }

　　注解：这一部分代码挺有讲究，写的很巧妙，这里谈谈我的理解。讲解代码时候是分为三种情况来说明的，其实第二种和第三种可以合并，因为第三种情况相当于与好后缀匹配的最长前缀长度为0。由于我们的目的是获得精确的bmGs[i]，故而若一个 字符同时符合上述三种情况中的几种，那么我们选取最小的bmGs[i]。比如当模式传中既有子串可以匹配上好后串，又有前缀可以匹配好后串的后串，那么此 时我们应该按照前者来移动模式串，也就是bmGs[i]较小的那种情况。故而每次修改bmGs[i]都应该使其变小，记住这一点，很重要！而在这三种情况中第三种情况获得的bmGs[i]值大于第二种大于第一种。故而写代码的时候我们先计算第三种情况，再计算第二种情况，再计算第一种情况。为什么呢，因为对于同一个位置的多次修改只会使得bmGs[i]越来越小。

• 代码4-5行对应了第三种情况，7-11行对于第二种情况，12-13对应第三种情况。
• 第三种情况比较简单直接赋值m，这里就不多提了。
• 第二种情况有点意思，咱们细细的来品味一下。

　　　1. 为什么从后往前，也就是i从大到小？原因在于如果i,j(i>j)位置同时满足第二种情况，那么m-1-i<m-1-j，而第十行代码保证了每个位置最多只能被修改一次，故而应该赋值为m-1-i，这也说明了为什么要从后往前计算。

　　 ２. 第8行代码的意思是找到了合适的位置，为什么这么说呢？因为根据suff的定义，我们知道x[i+1-suff[i]…i]＝＝x[m-1-siff[i]…m-1],而suff[i]==i+1，我们知道x[i+1-suff[i]…i]=x[0,i],也就是前缀，满足第二种情况。

3. 第9-11行就是在对满足第二种情况下的赋值了。第十行确保了每个位置最多只能被修改一次。

• 第12-13行就是处理第一种情况了。为什么顺序从前到后呢，也就是i从小到大？原因在于如果suff[i]==suff[j]，i<j，那么m-1-i>m-1-j,我们应该取后者作为bmGs[m - 1 - suff[i]]的值。

　　再来重写一遍BM算法：

 1 void BM(char *x, int m, char *y, int n) {
 2    int i, j, bmGs[XSIZE], bmBc[ASIZE];
 3
 4    /* Preprocessing */
 5    preBmGs(x, m, bmGs);
 6    preBmBc(x, m, bmBc);
 7
 8    /* Searching */
 9    j = 0;
10    while (j <= n - m) {
11       for (i = m - 1; i >= 0 && x[i] == y[i + j]; --i);
12       if (i < 0) {
13          OUTPUT(j);
14          j += bmGs[0];
15       }
16       else
17          j += MAX(bmGs[i], bmBc[y[i + j]] - m + 1 + i);
18    }
19 }