聚类算法总结以及python代码实现

一、聚类（无监督）的目标

使同一类对象的相似度尽可能地大；不同类对象之间的相似度尽可能地小。

二、层次聚类

层次聚类算法实际上分为两类：自上而下或自下而上。自下而上的算法在一开始就将每个数据点视为一个单一的聚类，然后依次合并（或聚集）类，直到所有类合并成一个包含所有数据点的单一聚类。因此，自下而上的层次聚类称为合成聚类或HAC。聚类的层次结构用一棵树（或树状图）表示。树的根是收集所有样本的唯一聚类，而叶子是只有一个样本的聚类。在继续学习算法步骤之前，先查看下面的图表

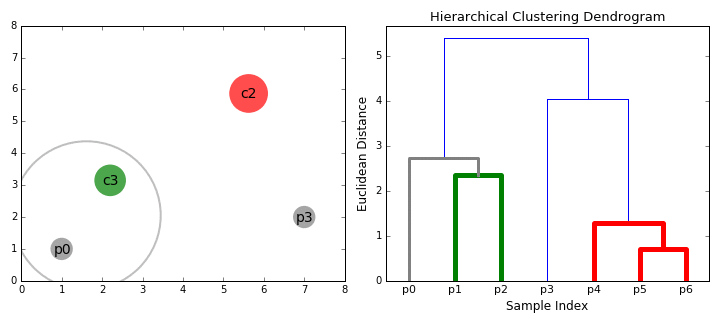
1.我们首先将每个数据点作为一个单独的聚类进行处理。如果我们的数据集有X个数据点，那么我们就有了X个聚类。然后我们选择一个度量两个聚类之间距离的距离度量。作为一个示例，我们将使用平均连接（average linkage）聚类，它定义了两个聚类之间的距离，即第一个聚类中的数据点和第二个聚类中的数据点之间的平均距离。

2.在每次迭代中，我们将两个聚类合并为一个。将两个聚类合并为具有最小平均连接的组。比如说根据我们选择的距离度量，这两个聚类之间的距离最小，因此是最相似的，应该组合在一起。

3.重复步骤2直到我们到达树的根。我们只有一个包含所有数据点的聚类。通过这种方式，我们可以选择最终需要多少个聚类，只需选择何时停止合并聚类，也就是我们停止建造这棵树的时候！

层次聚类算法不要求我们指定聚类的数量，我们甚至可以选择哪个聚类看起来最好。此外，该算法对距离度量的选择不敏感;它们的工作方式都很好，而对于其他聚类算法，距离度量的选择是至关重要的。层次聚类方法的一个特别好的用例是，当底层数据具有层次结构时，你可以恢复层次结构;而其他的聚类算法无法做到这一点。层次聚类的优点是以低效率为代价的，因为它具有O(n³)的时间复杂度，与K-Means和高斯混合模型的线性复杂度不同。

层次聚类方法对给定的数据集进行层次的分解，直到某种条件满足或者达到最大迭代次数。具体又可分为：

凝聚的层次聚类（AGNES算法）：一种自底向上的策略，首先将每个对象作为一个簇，然后合并这些原子簇为越来越大的簇（一般是计算所有簇的中心之间的距离，选取距离最小的两个簇合并），直到某个终结条件被满足或者达到最大迭代次数。
分裂的层次聚类（DIANA算法）：采用自顶向下的策略，它首先将所有对象置于一个簇中，然后逐渐细分为越来越小的簇（一般是每次迭代分裂一个簇为两个），直到达到了某个终结条件或者达到最大迭代次数。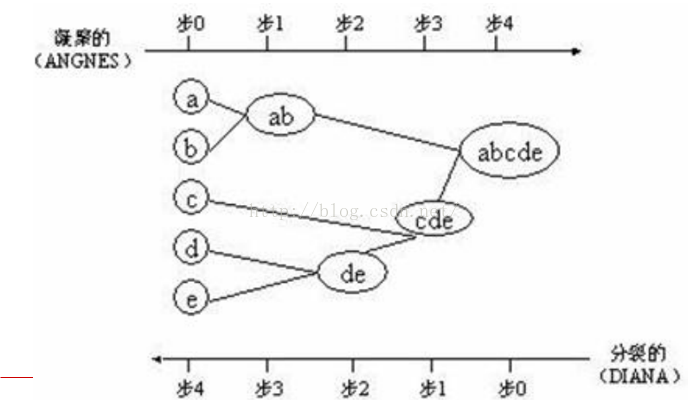

import sys,os
import numpy as np

class Hierarchical:
    def __init__(self,center,left=None,right=None,flag=None,distance=0.0):
        self.center = center
        self.left = left
        self.right = right
        self.flag = flag
        self.distance = distance

def traverse(node):
        if node.left==None and node.right==None:
            return [node.center]
        else:
            return traverse(node.left)+traverse(node.right)

def distance(v1,v2):
    if len(v1)!=len(v2):
        print("出现错误了")
    distance = 0
    for i in range(len(v1)):
        distance+=(v1[i]-v2[i])**2
    distance = np.sqrt(distance)
    return distance

def hcluster(data,n):
    if len(data)<=0:
        print('invalid data')
    clusters = [Hierarchical(data[i],flag=i) for i in range(len(data))]
    #print(clusters)
    distances = {}
    min_id1 = None
    min_id2 = None
    currentCluster = -1

    while len(clusters)>n:
        minDist = 100000000000000

        for i in range(len(clusters)-1):
            for j in range(i+1,len(clusters)):
                #print(distances.get((clusters[i], clusters[j])))
                if distances.get((clusters[i],clusters[j]))==None:

                    distances[(clusters[i].flag,clusters[j].flag)]=distance(clusters[i].center,clusters[j].center)

                if distances[(clusters[i].flag,clusters[j].flag)]<= minDist:
                    min_id1 = i
                    min_id2 = j
                    minDist = distances[(clusters[i].flag,clusters[j].flag)]

        if min_id1!=None and min_id2!=None and minDist!=1000000000:
            newCenter = [(clusters[min_id1].center[i]+clusters[min_id2].center[i])/2 for i in range(len(clusters[min_id2].center))]
            newFlag = currentCluster
            currentCluster -= 1
            newCluster = Hierarchical(newCenter,clusters[min_id1],clusters[min_id2],newFlag,minDist)
            del clusters[min_id2]
            del clusters[min_id1]
            clusters.append(newCluster)
        finalCluster = [traverse(clusters[i]) for i in range(len(clusters))]
        return finalCluster

if __name__ == '__main__':
    data = [[123,321,434,4325,345345],[23124,141241,434234,9837489,34743],\
            [128937,127,12381,424,8945],[322,4348,5040,8189,2348],\
            [51249,42190,2713,2319,4328],[13957,1871829,8712847,34589,30945],
            [1234,45094,23409,13495,348052],[49853,3847,4728,4059,5389]]
    #print(len(data))
    finalCluster = hcluster(data,3)
    print(finalCluster)
    #print(len(finalCluster[0]))

在聚类过程中，基于相关系数的距离是区分价格指数序列的主要指标，而 Ｍａｎｈａｔｔａｎ距离则用于处理相关系数无法区分的部分。分裂的层次聚类方法优于凝聚的层次聚类方法，因为凝聚的方法无法判断使用何种距离度量，而分裂的方法则依次使用基于相关系数的距离和 Ｍａｎｈａｔｔａｎ距离

【褚洪洋,柴跃廷,刘义.基于层次分裂算法的价格指数序列聚类[J].清华大学学报(自然科学版),2015,55(11):1178-1183.】大家可以参考这个文献对比层次聚类中的这两算法。论文的主要内容。

（该文提出一种基于层次分裂算法的价格指数序列聚类方法，选择基于相关系数的距离和 Ｍａｎｈａｔｔａｎ距 离 作 为 距 离 度 量，分 两 步 对 价格指数序列进行聚类。算法通过设置不同的终止条件停止分裂，不需要事先设置簇数。

本文提出一种价格指数序列的层次分裂算法，使用基于相关系数的距 离和 Ｍａｎｈａｔｔａｎ 距离作为距离度量，分两步对价格指数序列进行聚类。在编制网购价格指数时，

算法能够有效划分价格指数序列，找到同类商品的基本价格指数，为分类价格指数的编制提供依据。与其他时序数据的聚类算法相比，本算法有如下特点：

                          １）不直接采用相关系数作为距离度量，而是采用剔除整体趋势后的相关系数，能够更准确地反映价格指数序列间的关系；

                       ２）结合价格指数序列的实际情况，分别采用两种不同的距离度量对价格指 数序列进行分裂聚类，有效地对价格指数序列进行划分；

                       ３）不需要事先设置簇数，通过分裂终止条件控制簇分裂的停止，算法根据价格指数序列数据和终止条件参数自动获取簇数。）

三、基于密度的聚类方法
基于密度的聚类算法从样本密度的角度考察样本之间的可连接性，并基于可连接样本不断扩展聚类簇得到最终结果。
DBSCAN：具有噪声的基于聚类方法，能够处理非球状结构数据

 

大致思想如下：

初始化核心对象集合T为空，遍历一遍样本集D中所有的样本，计算每个样本点的ε-邻域中包含样本的个数，如果个数大于等于MinPts，则将该样本点加入到核心对象集合中。初始化聚类簇数k = 0， 初始化未访问样本集和为P = D。
当T集合中存在样本时执行如下步骤：
2.1记录当前未访问集合P_old = P
2.2从T中随机选一个核心对象o,初始化一个队列Q = [o]
2.3P = P-o(从T中删除o)
2.4当Q中存在样本时执行：
2.4.1取出队列中的首个样本q
2.4.2计算q的ε-邻域中包含样本的个数，如果大于等于MinPts，则令S为q的ε-邻域与P的交集，
Q = Q+S, P = P-S
2.5 k = k + 1,生成聚类簇为Ck = P_old - P
2.6 T = T - Ck
划分为C= {C1, C2, ……, Ck}

import numpy as np
import pylab as pl

data = '''
1,0.697,0.46,2,0.774,0.376,3,0.634,0.264,4,0.608,0.318,5,0.556,0.215,
6,0.403,0.237,7,0.481,0.149,8,0.437,0.211,9,0.666,0.091,10,0.243,0.267,
11,0.245,0.057,12,0.343,0.099,13,0.639,0.161,14,0.657,0.198,15,0.36,0.37,
16,0.593,0.042,17,0.719,0.103,18,0.359,0.188,19,0.339,0.241,20,0.282,0.257,
21,0.748,0.232,22,0.714,0.346,23,0.483,0.312,24,0.478,0.437,25,0.525,0.369,
26,0.751,0.489,27,0.532,0.472,28,0.473,0.376,29,0.725,0.445,30,0.446,0.459'''

a = data.split(',')
dataset = [(float(a[i]),float(a[i+1])) for i in range(1,len(a)-1,3)]

#计算欧几里得距离,a,b分别为两个元组
def dist(a,b):
    return np.sqrt(pow((a[0]-b[0]),2))+np.sqrt(pow((a[1]-b[1]),2))

def DBSCAN(D,e,Minpts):# 初始化核心对象集合T,聚类个数k,聚类集合C, 未访问集合P
    T =set();k=0;C = [];P = set(D)
    for d in D:
        if len([i for i in D if dist(d,i)<=e])>= Minpts:
            T.add(d)
    #开始聚类
    while len(T):
        P_old = P
        o = list(T)[np.random.randint(0,len(T))]
        P = P - set(o)
        Q = [];Q.append(o)
        while len(Q):
            q = Q[0]
            Nq = [i for i in D if dist(q,i)<=e]
            if len(Nq)>=Minpts:
                S = P&set(Nq)
                Q += (list(S))
                P = P - S
            Q.remove(q)
        k += 1
        Ck = list(P_old-P)
        T = T - set(Ck)
        C.append(Ck)
    return C

#画图
def draw(C):
    colValue = ['r', 'y', 'g', 'b', 'c', 'k', 'm']
    for i in range(len(C)):
        coo_X = []    #x坐标列表
        coo_Y = []    #y坐标列表
        for j in range(len(C[i])):
            coo_X.append(C[i][j][0])
            coo_Y.append(C[i][j][1])
        pl.scatter(coo_X, coo_Y, marker='x', color=colValue[i%len(colValue)], label=i)

    pl.legend(loc='upper right')
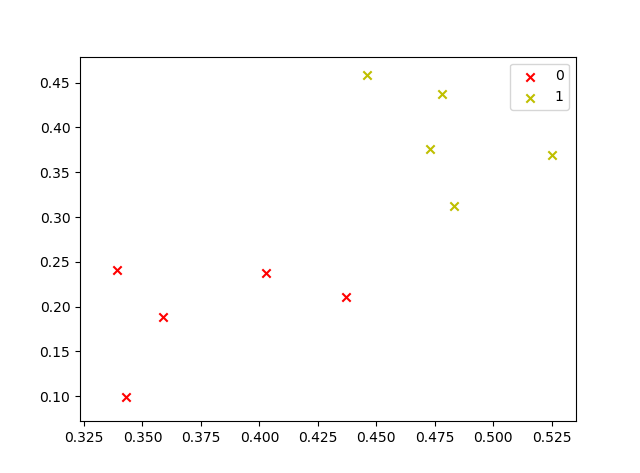
    pl.show()

C = DBSCAN(dataset, 0.11, 5)
draw(C)
运行结果如下：