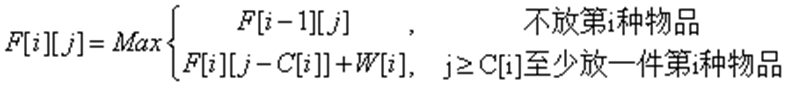包子凑数(dp 0-1、完全背包)【背包问题】
包子凑数(蓝桥杯)
题目描述
小明几乎每天早晨都会在一家包子铺吃早餐。他发现这家包子铺有N种蒸笼,其中第i种蒸笼恰好能放Ai个包子。每种蒸笼都有非常多笼,可以认为是无限笼。
每当有顾客想买X个包子,卖包子的大叔就会迅速选出若干笼包子来,使得这若干笼中恰好一共有X个包子。比如一共有3种蒸笼,分别能放3、4和5个包子。当顾客想买11个包子时,大叔就会选2笼3个的再加1笼5个的(也可能选出1笼3个的再加2笼4个的)。
当然有时包子大叔无论如何也凑不出顾客想买的数量。比如一共有3种蒸笼,分别能放4、5和6个包子。而顾客想买7个包子时,大叔就凑不出来了。
小明想知道一共有多少种数目是包子大叔凑不出来的。第一个例子:
2
4
5输出:
6
输入
第一行包含一个整数N。(1 <= N <= 100)
以下N行每行包含一个整数Ai。(1 <= Ai <= 100)输出
一个整数代表答案。如果凑不出的数目有无限多个,输出INF。
样例输入
2
4
6
样例输出INF
提示对于样例1,凑不出的数目包括:1, 2, 3, 6, 7, 11。
对于样例2,所有奇数都凑不出来,所以有无限多个。
思路:
题目说明了包子笼数假设有无限个 想到是完全背包(所有物品种类数假设有无限个)
补充:
1、0-1背包dp: (每种物品只有1个)
例题:
有重量分别为16 15 15 的三个物品 其价值分别为 30 25 25 要将他们装进承载重量最大为30的包中 计算最大价值是多少?(用dp解决这个问题)
s[i][j] 表示 遍历第i个物品 剩余背包容量为 j
代码如下:
#include<bits/stdc++.h>using namespace std;int w[5]={16,15,15},v[5]={30,25,25},dp[55][55];int main(){int n=3,m=30,maxx=-100;for(int i=0;i<n;i++){for(int j=0;j<=m;j++){if(j>=w[i]){dp[i][j]=max(dp[i-1][j],dp[i-1][j-w[i]]+v[i]);}else{dp[i][j]=dp[i-1][j];}if(dp[i][j]>maxx){ //或者是将判断删去 改为直接最后输出dp[n-1][m];maxx=dp[i][j];}}}printf("%d\n",maxx);return 0;}
2、完全背包dp:
例题 :
重量分别为2 4 8 3价值分别为5 9 18 9 的四件物品 每种物品数量有无限个 背包容量为10 计算最大价值:
· 注意和0-1 背包的区别:
例如:有重量为2的物品, dp[i][2]的时候放了一件了,当dp[i][4]的时候,dp[i][4]=max(dp[i-1][4],dp[i][4-2]+w[i]) 最多放一件
代码如下:
#include<bits/stdc++.h>using namespace std;const int maxn=105;int dp[maxn][55];int w[maxn+5],v[maxn+5];int n,m;int main(){int i,j,k;while(~scanf("%d %d",&n,&m)){memset(dp,0,sizeof(dp));for(i=1;i<=n;i++){scanf("%d %d",&w[i],&v[i]);}for(i=1;i<=n;i++){for(j=0;j<=m;j++){if(j>=w[i]){dp[i][j]=max(dp[i-1][j],dp[i][j-w[i]]+v[i]);//注意和01背包的区别,这里是dp[i][j-need[i]]+value[i]}else{dp[i][j]=dp[i-1][j];}}}printf("%d\n",dp[n-1][m]);}return 0;}
这个题和上面有点差别 没有价格的区别所以我开始就把物品重量当成价值 最后判断背包是否被填满 但是数目大了就会错误 不得不放弃 看了@ Statusrank的讲解才明白我想复杂了 链接(点击)
先遍历每个a[i] 然后将对应的dp值改变
往后再遍历的时候 直接dp[j]=dp[ j-a[i] ]
例如 :
a1=4,a2=5:前提 令dp[0]=1(下面解释为甚麽)
先遍历4 将 4和其倍数的值变为1 因为dp[j]=dp[ j-a[i] ]
当j=4时 dp[4]=dp[4-a[1]]=dp[0]=1;
再遍历5的时候会将5 的倍数变为1(同理)
同时 当j=9时: dp[9]=dp[9-a[2]]=dp[4]=1; 也会将其他5 和4组成的数的dp赋值为1
AC代码:
#include<bits/stdc++.h>using namespace std;const int MAX=1e5;int dp[MAX+5],a[105];int main(){int n,count=0;scanf("%d",&n);for(int i=0;i<n;i++){scanf("%d",&a[i]);if(a[i]%2==0){count++;}}if(count==n){printf("INF\n");}else{count=0;dp[0]=1;for(int i=0;i<n;i++){for(int j=a[i];j<=MAX+5;j++){dp[j]=max(dp[j],dp[j-a[i]]);}}for(int i=1;i<MAX+5;i++){if(dp[i]==0){count++;}}printf("%d\n",count);}return 0;}
包子凑数(dp 0-1、完全背包)【背包问题】的更多相关文章
- 包子凑数(dp思想)
问题描述: 小明几乎每天早晨都会在一家包子铺吃早餐.他发现这家包子铺有N种蒸笼,其中第i种蒸笼恰好能放Ai个包子.每种蒸笼都有非常多笼,可以认为是无限笼.每当有顾客想买X个包子,卖包子的大叔就会迅速选 ...
- DP大作战——多重背包
题目描述 在之前的上机中,零崎已经出过了01背包和完全背包,也介绍了使用-1初始化容量限定背包必须装满这种小技巧,接下来的背包问题相对有些难度,可以说是01背包和完全背包的进阶问题. 多重背包:物品可 ...
- 水dp第二天(背包有关)
水dp第二天(背包有关) 标签: dp poj_3624 题意:裸的01背包 注意:这种题要注意两个问题,一个是要看清楚数组要开的范围大小,然后考虑需要空间优化吗,还有事用int还是long long ...
- dp之多维背包hdu2159
二维背包问题,我是觉得这个题目数据比较水,虽然它最后说了怪可以无限个,但是它却只能最多杀s个,也就是所有品种的怪最多为s个,那么就是二维完全背包的问题了.......同时,它没有说一定要杀s只怪,所以 ...
- c++_包子凑数
标题:包子凑数 小明几乎每天早晨都会在一家包子铺吃早餐.他发现这家包子铺有N种蒸笼,其中第i种蒸笼恰好能放Ai个包子.每种蒸笼都有非常多笼,可以认为是无限笼. 每当有顾客想买X个包子,卖包子的大叔就会 ...
- Java实现第八届蓝桥杯包子凑数
包子凑数 题目描述 小明几乎每天早晨都会在一家包子铺吃早餐.他发现这家包子铺有N种蒸笼,其中第i种蒸笼恰好能放Ai个包子.每种蒸笼都有非常多笼,可以认为是无限笼. 每当有顾客想买X个包子,卖包子的大叔 ...
- DP大作战—组合背包
题目描述 组合背包:有的物品只可以取一次(01背包),有的物品可以取无限次(完全背包),有的物品可以取的次数有一个上限(多重背包). DD大牛的伪代码 for i = 1 to N if 第i件物品属 ...
- 树形DP(01组合背包The Ghost Blows Light HDU4276)
题意:有n个房间,之间用n-1条道路连接,每个房间都有一个定时炸弹,在T时间后会一起爆炸,第i个房间有pi价值的珠宝,经过每条道路都需要花费一定的时间,一个人从1房间开始 ,从n房间出去,保证再不炸死 ...
- dp之二维背包poj1837(天平问题 推荐)
题意:给你c(2<=c<=20)个挂钩,g(2<=g<=20)个砝码,求在将所有砝码(砝码重1~~25)挂到天平(天平长 -15~~15)上,并使得天平平衡的方法数..... ...
随机推荐
- Java Number & Math类
java Number类 Java的内置数据类型有byte.int.long.double等. Java 语言为每一个内置数据类型提供了对应的包装类. int对应的包装类为Integer long对应 ...
- 【Redis】String应用场景
单值缓存 SET key value GET key 对象缓存 SET user: value(json格式数据) MSET user::name value1 user::balance value ...
- PHP的图像函数
imagecreate() 和 imagecreatetruecolor() 函数用于创建一幅空白图像. imagedestroy() 函数用于销毁图像资源. imagecreate() 如果我们要对 ...
- Kivy主窗体大小的控制
1. 引入依赖模块 主窗体大小的控制,需要使用到kivy.core.window中的Window模块 from kivy.app import App from kivy.core.window im ...
- Android系统签名简介
apk的签名,简单说开发者可以通过签名 对应用进行标识和更新.包名在一个设备上是唯一的,这样可以避免被相同包名应用随意覆盖安装.这是一个非常重要的安全功能.系统中的签名文件,也是对系统中应用进行签名, ...
- sql注入讲解
1.输入1' 发现数据库报错,原因是我们的输入直接被代入到数据库查询语句里面. 2.有没有办法可以不让他报错呢?可以尝试一下构造正确的数据库语法,使之不报错.比如输入 1 and 1=1 试试 sel ...
- [PHP学习教程 - 网络]002.$_SERVER["SCRIPT_NAME"]、$_SERVER["PHP_SELF"]、$_SERVER["QUERY_STRING"]、$_SERVER["REQUEST_URI"]介绍($_SERVER URL Infomation)
引言:在使用原生PHP的时候,对于URL路径的切割,如:域名,查询参数等等的提取,通常绝大多数兄弟会忽略$_SERVER中定义的内置常量的关系,这里为大家讲解一下. 常用的URL请求路径$_SERVE ...
- [Objective-C] 006_Protocol(协议)
学过java的同学都知道Interface(接口),那么在Objective-C中有没有接口呢?其实 Objective-C中用Protocol(协议)来实现的,在Objective-C具体怎么用,我 ...
- Java中的集合(十一) 实现Map接口的TreeMap
Java中的集合(十一) 实现Map接口的TreeMap 一.TreeMap简介(基于JDK1.8) TreeMap是基于红黑树数据结构,是一个key-value的有序集合,该映射根据其键的自然顺序进 ...
- Weblogic 漏洞利用总结
整理的一些利用方式,后续会更新到15年至今的洞 后台爆破拿shell 后台爆破: 部署-安装-上载文件 制作war包,一直下一步,最好保存 jar -cvf shell.war ./shll/* 上传 ...