c#,pagerank算法实现一

PageRank让链接来"投票"

一个页面的“得票数”由所有链向它的页面的重要性来决定，到一个页面的超链接相当于对该页投一票。一个页面的PageRank是由所有链向它的页面（“链入页面”）的重要性经过递归算法得到的。一个有较多链入的页面会有较高的等级，相反如果一个页面没有任何链入页面，那么它没有等级。
　　2005年初，Google为网页链接推出一项新属性nofollow，使得网站管理员和网站作者可以做出一些Google不计票的链接，也就是说这些链接不算作"投票"。nofollow的设置可以抵制评论垃圾。

假设一个由4个页面组成的小团体：A，B，C和D。如果所有页面都链向A，那么A的PR（PageRank）值将是B，C及D的Pagerank总和。

继续假设B也有链接到C，并且D也有链接到包括A的3个页面。一个页面不能投票2次。所以B给每个页面半票。以同样的逻辑，D投出的票只有三分之一算到了A的PageRank上。

换句话说，根据链出总数平分一个页面的PR值。

最后，所有这些被换算为一个百分比再乘上一个系数。由于“没有向外链接的页面”传递出去的PageRank会是0，所以，Google通过数学系统给了每个页面一个最小值：

说明：在Sergey Brin和Lawrence Page的1998年原文中给每一个页面设定的最小值是1-d，而不是这里的

(1-d)/N。 所以一个页面的PageRank是由其他页面的PageRank计算得到。Google不断的重复计算每个页面的PageRank。如果给每个页面一个随机PageRank值（非0），那么经过不断的重复计算，这些页面的PR值会趋向于稳定，也就是收敛的状态。这就是搜索引擎使用它的原因。

实验数据a.txt是小的随机生成的图(图中没有终止点)。节点个数n=1000,边数m=8192

该图有一个1000条边构成的有向环(遍历了所有的节点)，这确保了该图是连通的。显然，这样的一个有向环确保了该图中没有终止点（即任何一个点都有出边）。如果存在一对节点之间有多条相同的有向边，你的算法应该把它们当做是同一条边。a.txt的每一行表示一条有向边，第一列表示边的源结点，第二列表示边的目的节点。

l 实现过程：

设有向图 G=(V,E)有n个节点(编号为1,2,...N)和M条边，所有的节点都有至少一个出边，且M=[Mji](n*n)是一个m*n的随机邻接矩阵，定义如下：对任意i,j€[1,n]

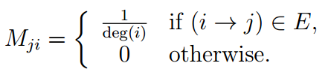
里，deg(i)是图G中节点i的出边个数。基于PageRank的定义，设1-Β为随机跳转概率，我们将PageRank向量记为r，有如下等式

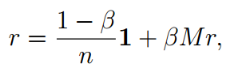
基于上面的公式，计算PageRank向量的迭代过程如下：

矩阵运算调用了 MathNet.Numerics

  public static double[,] Get()
         {
             double[,] m = new double[, ];
             for (int i = ; i < ; i++)
             {
                 for (int j = ; j < ; j++)
                 {
                     m[i, j] = ;
                 }
             }
             double[] s = new double[];
             double[,] M = new double[, ];
             for (int i = ; i < ; i++)
             {
                 for (int j = ; j < ; j++)
                 {
                     M[i, j] = ;
                 }

             }
             StreamReader sr = File.OpenText(@"E:\a.txt");
             string nextLine;
             while ((nextLine = sr.ReadLine()) != null)
             {
                 char[] charTemp = { '\t' };
                 string[] arr = nextLine.Split(charTemp);
                 int[] d = Array.ConvertAll(arr, int.Parse);
                 int a1 = d[] - ;
                 int a2 = d[] - ;
                 m[a1, a2] = ;
             }
             sr.Close();
             for (int i = ; i < ; i++)
             {
                 for (int j = ; j < ; j++)
                 {
                     s[i] += m[i, j];
                 }
             }
             for (int i = ; i < ; i++)
             {
                 for (int j = ; j < ; j++)
                 {
                     if (m[i, j] == )
                         M[j, i] = 1.0 / s[i];
                 }
             }
             return M;
         }
         public static double [] Getmtrix(double[,] M)
         {

             double num = 0.8;
             double[,] result = Get();
             var mb = Matrix<double>.Build;
             var A= mb.DenseOfArray(result);
             var matrixR = mb.Dense(, , 0.001);
             var matrixL = mb.Dense(, , 0.0002);
             for (int p = ; p < ; p++)
             {
                 matrixR = matrixL + (A * matrixR) * num;
             }
            double[,]b= matrixR.ToArray();
             double[] d = new double[b.Length];
             for (int i = ; i < b.Length; i++)
             {
                 for (int j = ; j < ; j++)
                 {
                     d[i] = b[i, j];
                 }
             }
             return d;
         }
         public static void show(double[] a)
         {
             double[] a1 = Getmtrix(Get());
             double max = ;
             int maxindex = -;
             for (int j = ; j < ; j++)
             {
                 max = a1.Max();
                 maxindex = Array.IndexOf(a1, max);
                 a1[maxindex] = ;
                 Console.WriteLine("最大:{0}" + "节点:{1}", j+, maxindex+);

             }

         }
         public static void show2(double[] a)
         {
             double[] a1 = Getmtrix(Get());
             for (int j = ; j < ; j++)
             {
                 double min = 1.0;
                 int minindex = -;
                 min = a1.Min();
                minindex = Array.IndexOf(a1, min);
                a1[minindex] = ;
                 Console.WriteLine("最小:{0}" + "节点:{1}", j + , minindex + );
             }
             Console.ReadKey();
         }
         static void Main(string[] args)
         {
             show(Getmtrix(Get()));
             show2(Getmtrix(Get()));

         }

pagerank算法

l 输出

ü PageRank分值最高的5个节点的id

ü PageRank分值最低的5个节点的id

l graph-full.txt