Java8大排序算法

一.冒泡排序

　 基本思想:通过对待排序序列此前向后,依次比较相邻元素的值,若发现逆序则进行交换,使得较大的值从前面移动到后面,

　　　　      类似于水下的气泡一样(是所有排序算法中效率最低的)

public static void BobbleSort(int[] arr){
        /*冒泡排序,时间复杂度为O(n^2)*/
        if (arr == null || arr.length == 0){
            return;
        }
        int temp = 0; // 临时变量,用于存放大的数
        boolean flag = false; // 是否进行过交换,默认为false
        for (int i = 0; i < arr.length-1;i++){ //需要遍历的次数
            for (int j = 0; j < arr.length-1-i;j++){ //遍历数组中的值,来比较
                if (arr[j] > arr[j+1]){ // 如果后面的数比前面的数要大,则进行交换
                    flag = true;//
                    temp = arr[j];
                    arr[j] = arr[j+1];
                    arr[j+1] = temp;
                }
            }
            if (!flag){ // 如果flag==false,表示没有进行过交换,直接退出即可
                break;
            }else{
                flag = false; // 要将flag重置,进行下一次的判断
            }

        }
    }
}

测试,使用80000个随机数来进行测试

public static void main(String[] args) {
        int[] array = createRandomArr(80000);
        showTime("排序开始时间");

        BobbleSort(array);
        showTime("排序结束时间");
    }

    public static void showTime(String str){
        Date d = new Date();
        SimpleDateFormat sdf = new SimpleDateFormat("yyyy-MM-dd HH:mm:ss");
        String dStr = sdf.format(d);
        System.out.println(str+": "+dStr);
    }

    public static int[] createRandomArr(int n){
        int[] arr = new int[n];
        for (int i = 0; i < n; i++) {
            arr[i] = (int)(Math.random() * 800000);
        }
        return arr;
    }

执行结果: 排序耗时9秒

二.选择排序

　 基本思想:第一次从arr[0]~arr[n-1]中选出最小值和arr[0]进行交换,第二次从a[1]~a[n-1]选出最小值和a[1]进行交换,第三次从a[2]~a[n-1]选出

　　　　　  最小值和a[2]进行交换,直到执行n-1次,得到一个排序码从小到大的有序序列

　　

public static void selectSort(int[] arr){
        /*选择排序*/
        if (arr.length == 0 || arr == null){return;}
        int minIndex = 0;
        int minValue = 0;
        for (int i = 0; i < arr.length-1; i++) {
            minIndex = i;   // 记录最小值的下标,从0开始
            minValue = arr[i]; // 记录最小值,假设是a[0]开始
            for (int j = i+1; j < arr.length;j++){ // 从i后开始循环
                if (minValue > arr[j]){ // 如果最小的值,并不是a[i],重置minIndex和minValue
                    minValue = arr[j]; // 获取最小值,和最小值的下标
                    minIndex = j;
                }
            }
            // 将最小的值放在a[i],比较并进行交换
            if (minIndex != i){
                arr[minIndex] = arr[i]; // 把a[0]第一个值先放在a[minIndex]处
                arr[i] = minValue; // 把保存下来的最小值回填到a[0],即找到了全局的最小值
            }
        }

    }

测试,使用80000个随机数来进行测试

执行结果: 排序耗时2秒

三.插入排序

　  基本思想:把n个待排列的元素看成一个有序表和一个无序表,开始时有序表中只包含一个元素,无序表中包含n-1个元素,排序过程中每次从无序表中抽取

　　　　　　第一个元素,将它的排序码依次与有序表元素的排序码进行比较,将其插入到有序表中的适当的位置,成为新的有序表

public static void insertSort(int[] array){
        /*插入排序*/
        if (array.length == 0 || array == null){return;}
        int insertVal = 0;
        int insertIdx = 0;

        for (int i = 1; i < array.length; i++) {
            // 定义待插入的数
            insertVal = array[i];// 从第二个数开始和第一个数进行比较
            insertIdx = i -1;     // 第一个数的下标
            // 给insertVal找到合适的位置
            // 1.insertIdx >=0保证给insertVal插入的位置不越界
            // 2.insertVal < array[insertIdx] 找到了待插入的数
            // 3.需要将arr[insertIdx]后移
            while (insertIdx >=0 && insertVal < array[insertIdx]){
                array[insertIdx+1] = array[insertIdx];
                insertIdx--;
            }
            // 退出while循环时候说明数已经找到,只要把保留下来的数放到前面即可
            if (insertIdx+1 != i){
                array[insertIdx+1] = insertVal;
            }

        }
    }

测试,使用80000个随机数来进行测试

执行结果: 排序耗时不到1秒

四.希尔排序

　  基本思想:当插入排序插入的数较小时,会导致频繁移动数组导致执行效率低下,希尔排序是一种优化的插入排序.它将数据按下标的一定增量分组

　　　　　　对每组直接进行简单插入排序,随着增量逐渐减少,每组包含的关键词就越多,当增量减少到1时,所有的数据都已排序完毕

public static void shellSort2(int[] arr){
        /*使用移位法进行希尔排序*/
        if (arr.length == 0 || arr == null){
            return;
        }
        int minVal = 0;  // 记录最小值
        int minIdx = 0;  // 记录最小值的下标
        for (int gap = arr.length/2; gap >0 ; gap/=2) { // 每次缩小遍历次数增量 每次折半,缩小增量
            for (int i = gap; i < arr.length; i++) { // 从gap个位置,逐步对其所在的元素进行插入排序
                minVal = arr[i]; // 假定最小值是arr[i]
                minIdx = i;   // 记录i
                //1.minIdx-gap >=0 确保插入的位置不会越界
                //2.minVal < arr[minIdx-gap] 找到了待插入的数
                while (minIdx-gap >=0 && minVal < arr[minIdx-gap]){
                    // 同插入排序
                    arr[minIdx] = arr[minIdx-gap];
                    minIdx-=gap;
                }
                arr[minIdx] = minVal;
            }
        }

    }

测试,使用80000个随机数来进行测试

执行结果: 排序耗时不到1秒

五.快速排序

　   基本思想:通过一趟排序将要排序的数据分割成独立的两个部分,其中一部分的数据比另一部分的数据都要小,然后在按照此方法对这两部分数据

　　　　　　 进行快速排序,整个排序通过递归实现,以此达到整个数据排列有序

/**
     * 快速排序
     * @param arr 需要排序的数组
     * @param left   左索引
     * @param right  右索引
     */
    public static void quickSort(int[] arr,int left,int right){
        if (arr.length == 0 || arr == null){return;}

        int l = left;
        int r = right;
        int temp = 0;  // 作为交换的临时变量
        int pivot = arr[(left+right)/2];   // 找到数组中间的值
        //while循环让比pivot值小的放在左边,比pivot值大的放在右边
        while (l<r){
            //在pivot的左边一直找,直到找到比pivot大的值就退出
            while (arr[l] < pivot){
                l+=1;
            }
            //在pivot的右边一直找,直到找到比pivot小的值就退出
            while (arr[r] > pivot){
                r-=1;
            }
            // 如果l>=r说明左右两边的值已经按照左边全是小于pivot,右边都是大于pivot的值来存放
            if (l >= r){
                break;
            }
            //交换
            temp = arr[l];
            arr[l] = arr[r];
            arr[r] = temp;

            // 如果交换完成后,发现pivot == arr[l],需要将r--,前移
            if (arr[l] == pivot){
                r-=1;
            }
            // 如果交换完成后,发现pivot == arr[r],需要将l++,后移
            if (arr[r] == pivot){
                l+=1;
            }
        }
        // 如果出现 l==r,必须要把l++,r--,否则会出现栈溢出
        if (l == r){
            l+=1;
            r-=1;
        }
        // 向左递归
        if (left < r){
            quickSort(arr,left,r);
        }
        // 向右递归
        if (right > l){
            quickSort(arr,l,right);
        }
    }

测试,使用80000个随机数来进行测试

执行结果: 排序耗时不到1秒

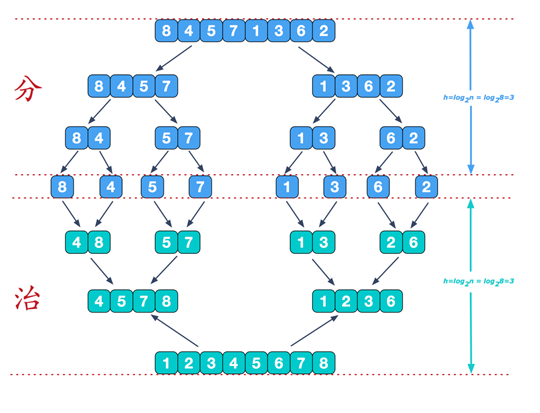
六.归并排序

　  基本思想:是利用归并的思想实现的排序的算法,该算法采用经典的分治策略.

　          　

    /**
     * 分割
     * @param arr  原数组
     * @param left  左下标
     * @param right 右下标
     * @param temp 临时数组
     */
    public static void mergeSort(int[] arr,int left,int right,int[] temp){
        if (left < right){
            int mid =( left+right )/2;
            // 向左递归
            mergeSort(arr,left,mid,temp);
            // 向右递归
            mergeSort(arr,mid+1,right,temp);
            // 合并
            merge(arr,left,mid,right,temp);
        }

    }

/**
     * 合并
     * @param arr 需要排序的原始数组
     * @param left 左边有序序列的初始索引
     * @param mid  中间索引
     * @param right 右边有序序列的初始索引
     * @param temp 临时数组
     */
    public static void merge(int[] arr,int left,int mid,int right,int[] temp){
        int i = left; // 初始化i,左边有序序列的初始索引
        int j = mid + 1; // 初始化j,右边有序序列的初始索引
        int t = 0; // 临时数组的索引

        /*1.将左右两边的有序数据按照规则填充到temp中,直到左右两边的有序序列有一边处理完为止*/
        while (i <= mid && j <= right){ // 继续
            if (arr[i] <= arr[j]){ //如果左边的有序序列当前的元素小于右边有序序列当前的元素
                temp[t] = arr[i]; // 将左边有序序列的元素填充到temp中
                t+=1;
                i+=1;
            }else{  //如果右边的有序序列当前的元素小于左边有序序列当前的元素
                temp[t] = arr[j];// 将右边有序序列的元素填充到temp中
                t+=1;
                j+=1;
            }
        }

        /*2.把剩余的数据的一边依次全部填充到temp中*/

        while (i<=mid){ // 左边的有效数据还有剩余就全部填充到temp中
            temp[t] = arr[i];
            t+=1;
            i+=1;
        }
        while (j <= right){ // 右边的有效数据还有剩余就全部填充到temp中
            temp[t] = arr[j];
            t+=1;
            j+=1;
        }

        /*3.将temp数组的元素拷贝到arr中,每次都要拷贝*/
        t = 0; // t要清空
        int tempLeft = left;
        while (tempLeft <= right){
            arr[tempLeft] = temp[t];
            t+=1;
            tempLeft+=1;
        }

    }

测试,使用80000个随机数来进行测试

执行结果: 排序耗时不到1秒

七.基数排序

　  基本思想:将所有待比较的数统一为同样的数位长度,数位较短的数前补零.然后从最低位开始,依次进行一次排序.这样从最低位排序一直到最高位排序完成后

　　　　　　数列就成了有序序列了.

public static void radixSort(int arr[]){
        /*基数排序算法*/
        if (arr.length == 0 || arr == null ){
            return;
        }
        /*1.找出数组中的最大的数*/
        int max = arr[0];
        for (int ele : arr) {
            if(ele > max){
                max = ele;
            }
        }

        /*2.确定最大数的长度,确定桶排序的循环次数*/
        int maxLength = (max+"").length();

        /*定义一个二维数组表示10个桶,每个桶就是一个一维数组
        * 1.二维数组中包含10个一维数组
        * 2.为了防止放数据导致数据溢出,则每一个一维桶的长度是arr.length
        * */
        int[][] bucket = new int[10][arr.length];

        /*记录每个桶中存放的有效数据的个数
        * 比如:bucketElementCount[0],记录的就是bucket[0]中元素的个数
        * */
        int[] bucketElementCount = new int[10];

        // n表示对数据的位数进行处理,第一次个位,第二次十位,第三次百位,以此类推
        for (int i = 0,n=1; i < maxLength; i++,n*=10) {
            for (int j = 0; j < arr.length; j++) {
                // 取出每个数对应的位数
                int digitOfElement = arr[j] / n % 10;
                // 放入到对应的桶中
                bucket[digitOfElement][bucketElementCount[digitOfElement]] = arr[j];
                bucketElementCount[digitOfElement]++;  // 每一个桶的记录数递增
            }

            /* 按照桶的顺序,放回到原来的数组*/
            int index = 0;
            //遍历每一个桶,并将桶的数据放回到原数组
            for (int k = 0; k < bucketElementCount.length; k++) {
                // 如果桶中有数据,才放入
                if (bucketElementCount[k] != 0){
                    // 循环第k个桶,放入
                    for (int l = 0; l < bucketElementCount[k]; l++) {
                        // 取出元素放入到原数组中
                        arr[index++] = bucket[k][l];
                    }
                }
                // 每次处理完成后,一定要记得将bucketElementCount[k]清空
                bucketElementCount[k] = 0;

            }

        }

    }

测试,使用80000个随机数来进行测试

执行结果: 排序耗时不到1秒

八.堆排序

　  基本思想:将待排序的序列构造成一个大顶堆.此时整个序列的最大值就是堆顶的根节点,把它和末尾的元素进行交换.此时末尾的元素就成了最大值.然后将剩余n-1个元素重新构造成一个

　　　　　　堆.如此反复执行就能到一个有序的序列

/**
     * 把一个二叉树,调整为大顶堆
     * @param array  待调整的数组
     * @param i      表示非叶子节点在数组中的索引
     * @param length 表示有多少个元素要调整,length逐渐在减少
     */
    public static void adjustHeap(int[] array,int i,int length){
        /*取出当前元素的值,保存在临时变量中*/
        int temp = array[i];
        /*开始进行调整*/
        /* k=2*i+1,k是i的左子节点*/
        for (int k = 2*i+1;k < length; k = k*2+1){
            /*如果左子节点的值小于右子节点的值*/
            if (k+1 < length && array[k] < array[k+1]){
                k++; // k指向右子节点
            }
            /*如果子节点大于父节点*/
            if (temp < array[k]){
                /*把较大的值赋给当前节点*/
                array[i] = array[k];
                /*i指向k,继续循环比较*/
                i = k;
            }else {
                break;
            }
        }
        /*当循环结束后,已经把i为父节点的数的最大值放在了顶部,所以此时把temp的值放在调整后的位置*/
        array[i] = temp;
    }

public static void heapSort(int[] array){
        if (array.length == 0 || array == null){
            System.out.println("数组为空,不能排序");
            return;
        }
        int temp = 0;
        /*把一个无序的序列构建成一个堆,根据升序和降序选择大顶堆还是小顶堆*/
        for (int i = array.length/2-1; i >= 0; i--) {
            adjustHeap(array,i,array.length);
        }

        /**
         * 1.将堆顶的元素和堆底的元素进行交换,把最大的元素放在数组的尾部
         * 2.重新调整结构,然后继续交换堆顶元素和当前末尾元素,反复执行,使得数组有序
         */
        for (int j = array.length-1; j > 0; j--) {
            /*交换*/
            temp = array[j];
            array[j] = array[0];
            array[0] = temp;
            adjustHeap(array,0,j);
        }

    }

测试,使用80000个随机数来进行测试

执行结果: 排序耗时不到1秒

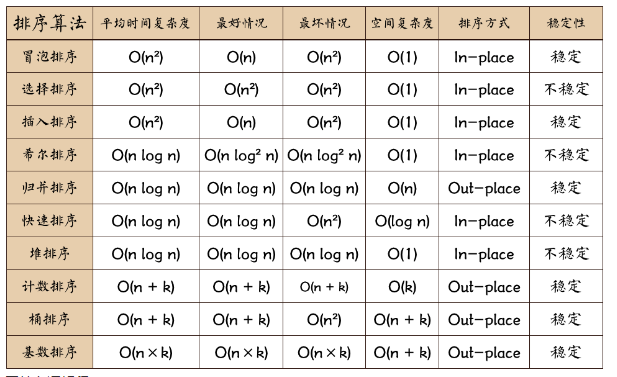
八大排序算法的时间复杂度,空间复杂的比较