Tips for traing DNN

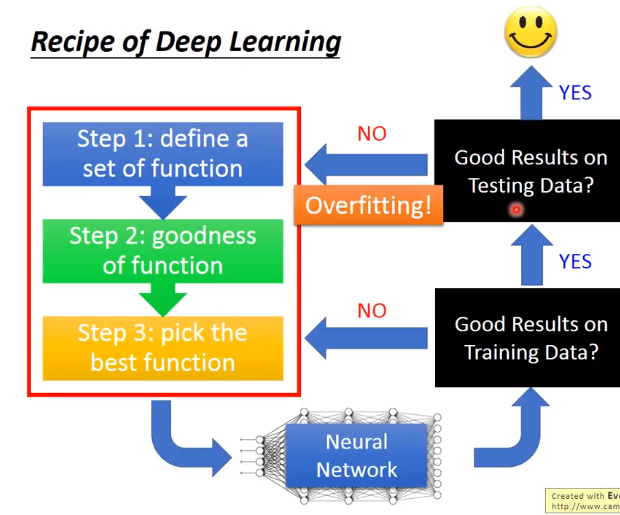
1。   一般的机器学习方法不会在train好的模型上检查training data的结果，因为DNN在training data上都没有办法获得很好的正确率，

所以要先回头看一下要对模型做什么修改，才能使得在training set上取得比较好的正确率。

2。  在training set获得好的结果，但在testing set上获得不好的结果，这个才是overfitting，并不是说在training set获得好的结果就是overfitting。

      这个时候要回去做一些工作解决overfitting这个问题。解决overfitting的同时会使得结果在training set上的结果性能变差，这个时候要回到注意1上。

上图中，56层的模型对比20层的模型，无论是在training set还是testing set上表现都要差，这个事情并不是Overfitting的原因，而是没有训练好（没训练好的原因：局部最小值，鞍点，平原）。
   但也不是 underfitting，模型的参数不够多，没有能力解决某一个问题。
  有意思的观点：56层的模型肯定要比20层的好，原因很简单，如果我56层前面20层和下面的20层一样，后面36层啥事也不做，至少来说他的性能要和下面的一样，因此结论就是56层的模型是没有训练好　　

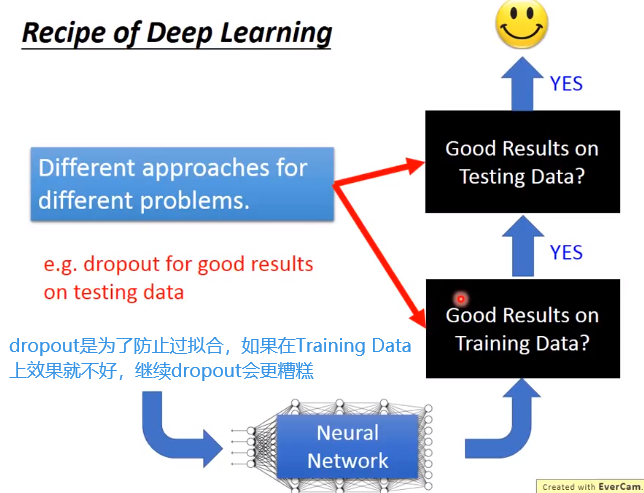
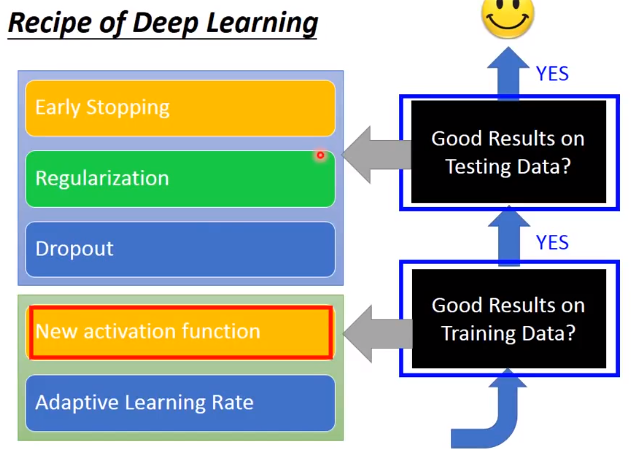
不同问题需要对应的方法来解决

Training data性能差

激活函数改进

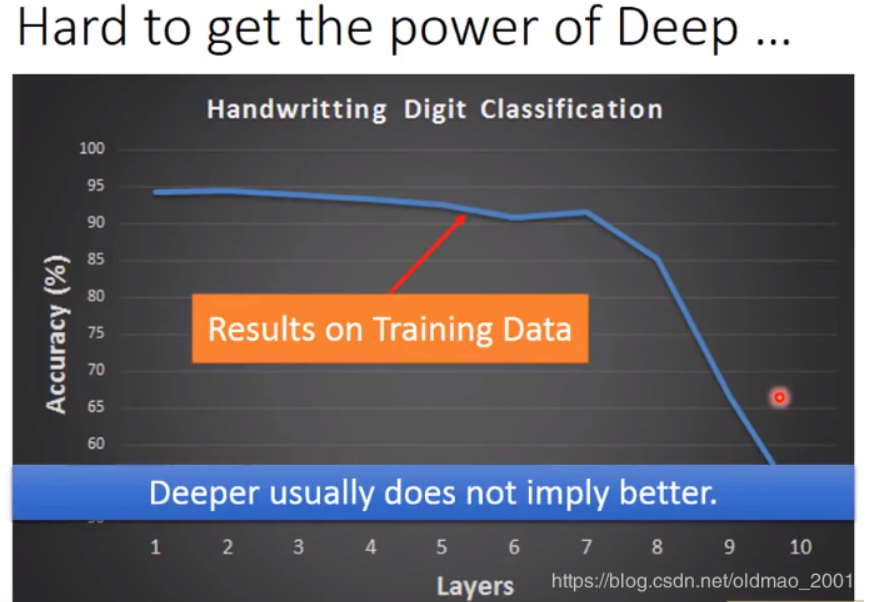
上面这个例子不是overfitting，如果是overfitting那么在training set获得好的结果，但在testing set上获得不好的结果。上面的曲线是training data的，在第七层的时候准确率就坏掉

那么为什么会这样呢？

首先用w变化对C的变化来表示derivatives

每通过一次sigmoid，output的变化都在衰减
因此，对input改变，其实对output（C）的影响很小

梯度消失：在输入层附近梯度小，在输出层梯度大，当参数还没有更新多少时，在输出层已经收敛了，这是激活函数sigmoidsigmoid对值压缩的问题。
也就是一个比较大的input进去，出来的output比较小，所以最后对total loss的影响比较小，趋于收敛。

Relu

z代表input
3.等同于无穷多的sigmoid(bias 不同)叠加的结果

那么如何vanish(消除) gradient problem

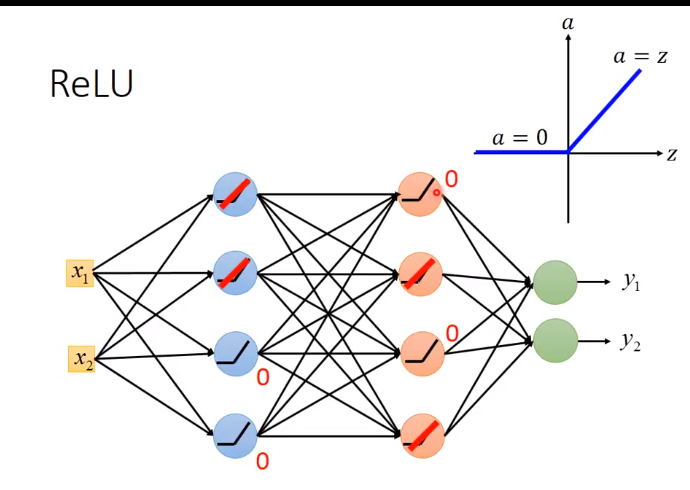
0可以从network 拿掉

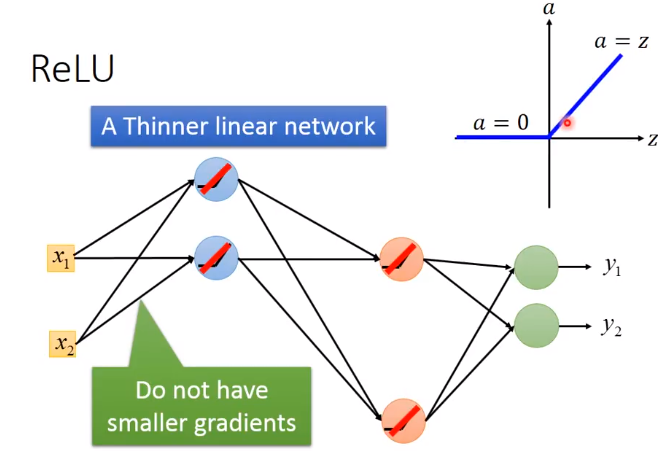
而之前说梯度递减也是因为sigmoid的衰减效果，而我们现在用ReLU它本身不会对增量进行递减，因为现在凡是在网络中work的神经元，其输出都等于其输入，相当于线性函数y=x。

问题：如果网络都用ReLU了，网络变成了线性的了？那NN的效果不会变得很差吗？这与我们使用深层网络的初衷不是违背了吗？

答：其实使用ReLU的NN整体还是非线性的。当每个神经元的操作域（operation region）是想相同的时，它是线性的。即当你对input只做小小的改变，不改变神经元的操作域，那NN就是线性的；

但如果对input做比较大的改变，改变了神经元的操作域，网络的架构也会变化，这样NN就是非线性的了。

另外一个问题：ReLU不能微分呀？怎么做梯度下降呀？

答：当x>0时，ReLU微分就是1，当x<0时，ReLU微分就是0。而x的值一般不太可能恰好是0，所以不在x=0时的微分值也没问题。

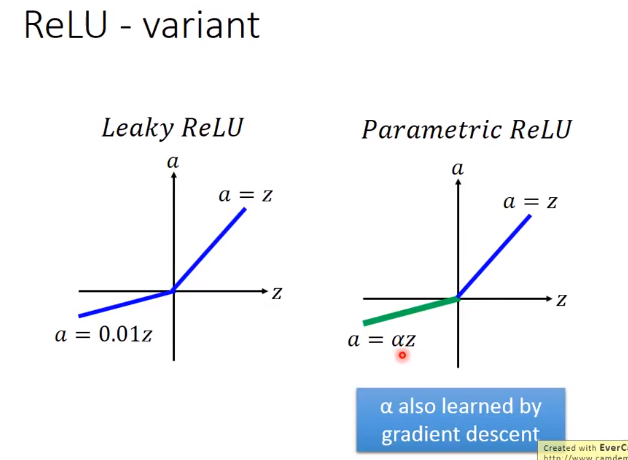
很简单，防止小于零的输入求导后为0。右边的进一步把0.01参数变成一个超参数。

Maxout

解释Relu 是Maxout的一个特例

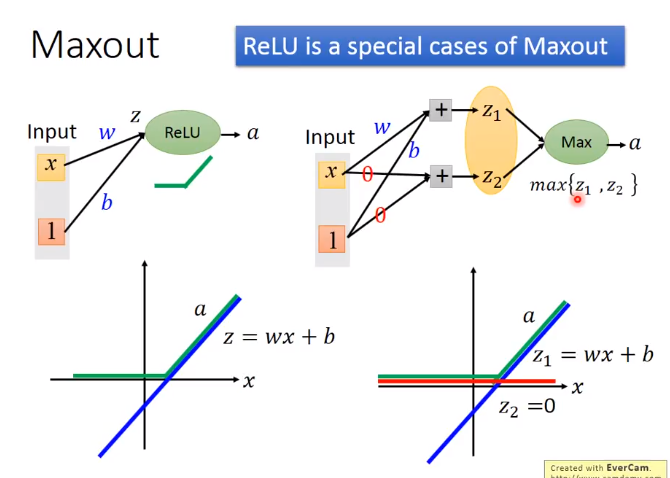
Maxout还有其他功能

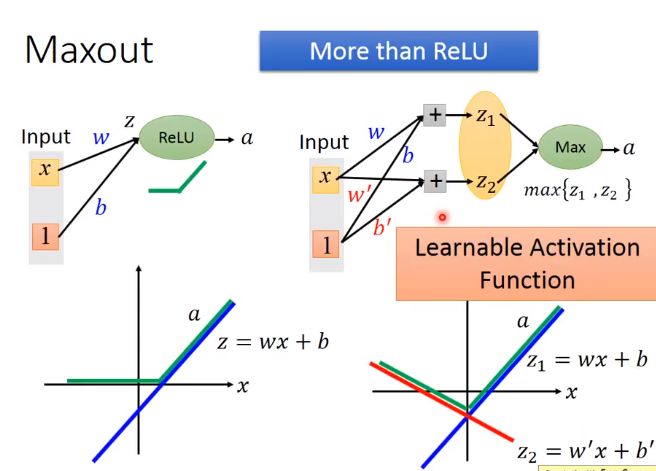
piecewise linear convex function：分段线性凸函数

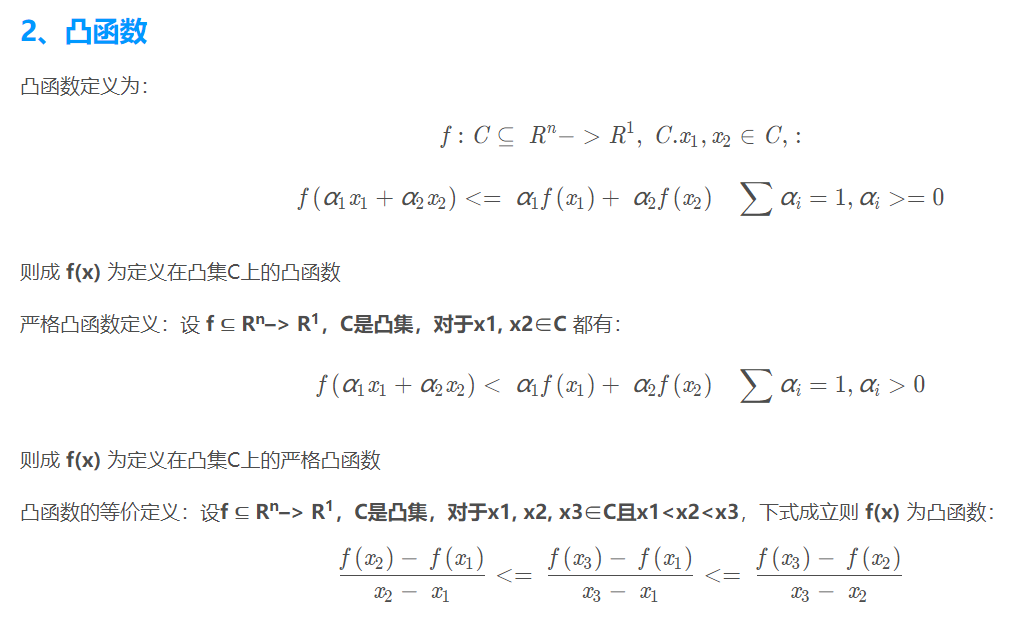
Training Maxout

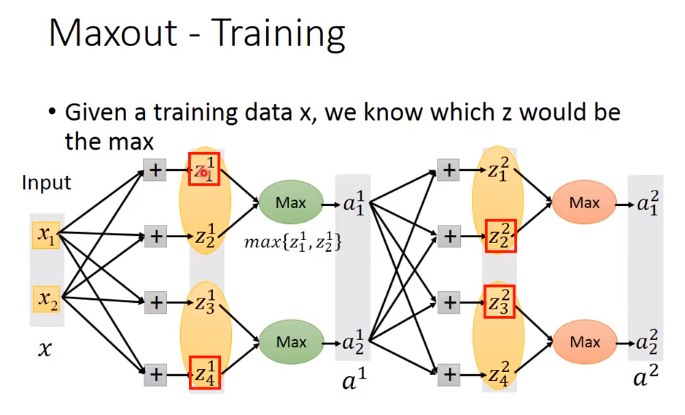
红色框中是group中大的那个，那么这个网络可以变成：

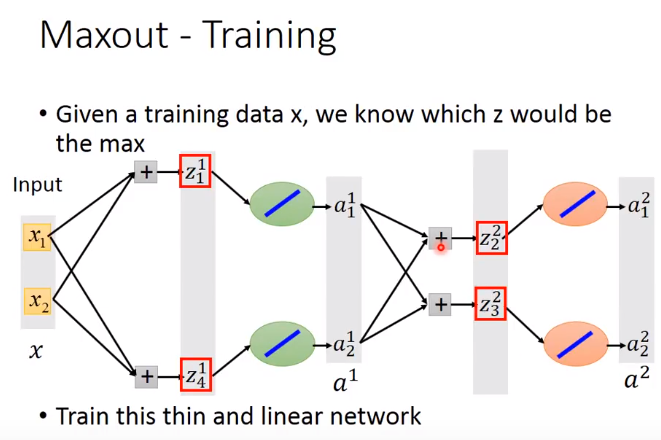
因为小的element是变为0，对网络无影响，可以去掉。这里也是一个thin and linear network。
那些没有被框起来的element是不是就没有办法被吹到？
不会，不同的输入的时候，group中的最大值是不一样的，我们的train set有很多笔data，每次不同的data输入，网络的结构都不一样，每个element都会被train到

Adagrad的优化RMSProp

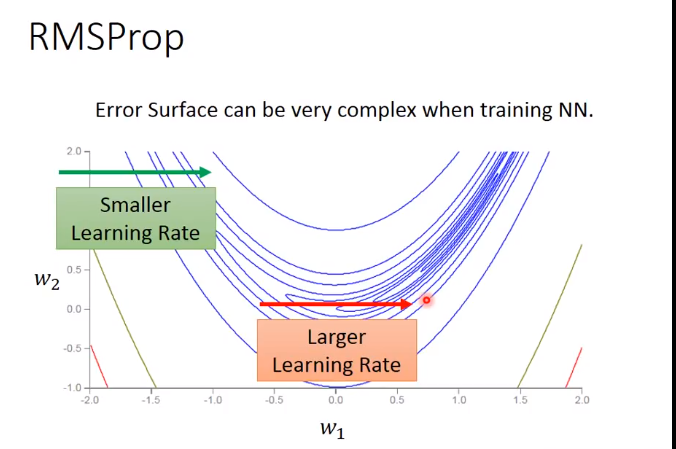
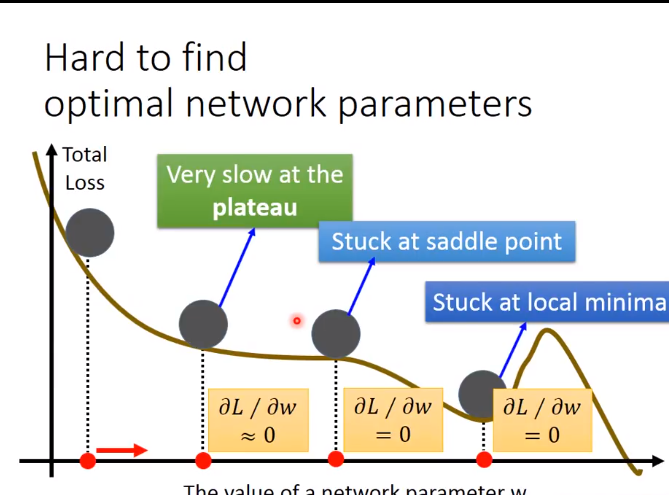
在复杂网络里面出现局部minima的几率很低，因为无论是局部还是全局的minima，在这个点上的各个dimension的偏导都为0，复杂网络中的dimension这么多，

所以同时出现这个情况的几率比中六合彩还低，所以一旦出现，就是全局minima

Momentum 推进力

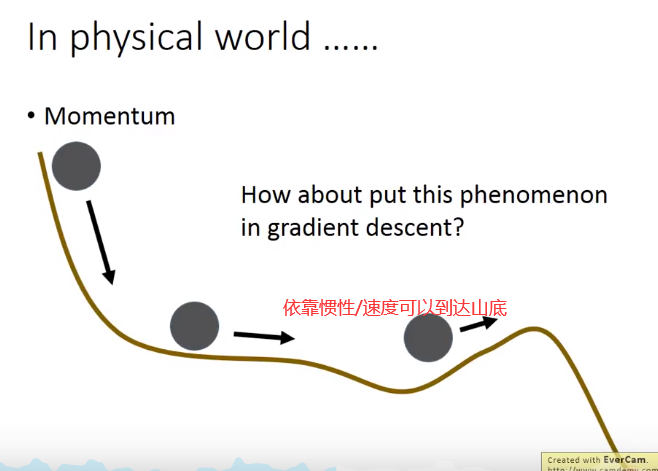
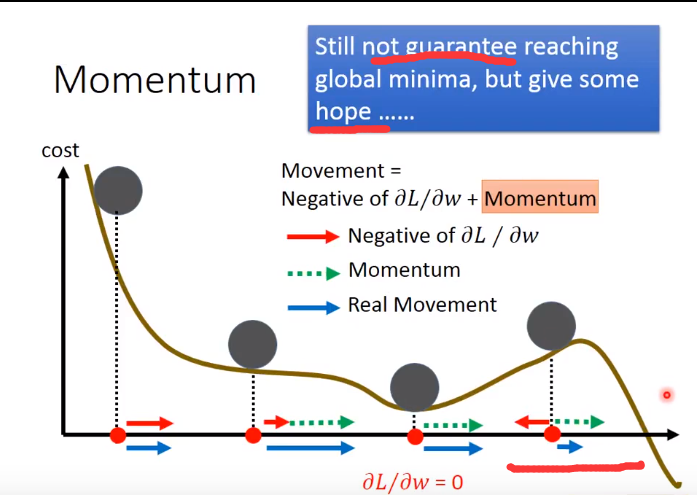
Momentum相当于利用指数加权平均给Loss function加入了一个惯性，RMSprop给△梯度加了摩擦力。

Adam

实际上是RMSProp + Momentum，

前面是train data 效果不好的方法，下面开始讲test data 出现问题时的方法

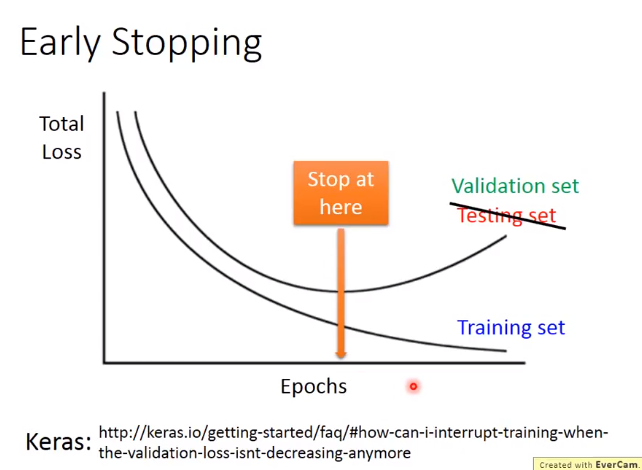
Early Stop

Regulation

每次都会让wt小些
1-lam*theta <1 (1-lam*theta)wt离0会越来越近

Regularization虽然在传统机器学习中有不错的表现，但在DNN中效果不怎么样，因为在DNN中初始化参数的时候参数会比较小（接近0），然后随着训练后慢慢变化（离0越来越远），

而Regularization如上图所示，它算法思想是希望参数不要离0太远，这个效果在DNN中等同于减少参数更新次数一样样。所以在SVM中是把Regularization显式写到算法中的，因为SVM可能是一次（没有迭代）就解出结果。

意思就是说DNN天生可以迭代，如果希望参数离0近一点，可以用减少更新次数来达到同样效果。

正则化：减弱权重差异，来削弱某些突出特征的显著程度，进而减少模型复杂性
L1:wt>0,就会减去lam*theta.wt<0,就会加上lam*theta。加减的是常量，
那么最后保留的有很多接近0的值，也会有很多大的值，分布离谱。L1可以产生稀疏模型（有些稀疏等于0）
L2:wt较大时，wt下降的也会快些。（（1-lam*theta）*wt大些）削弱特征特别强的权重以减少过拟合
相反wt很小时，下降的会很慢。（（1-lam*theta）*wt小些）因此最后会保留大都是很小的值

Dropout

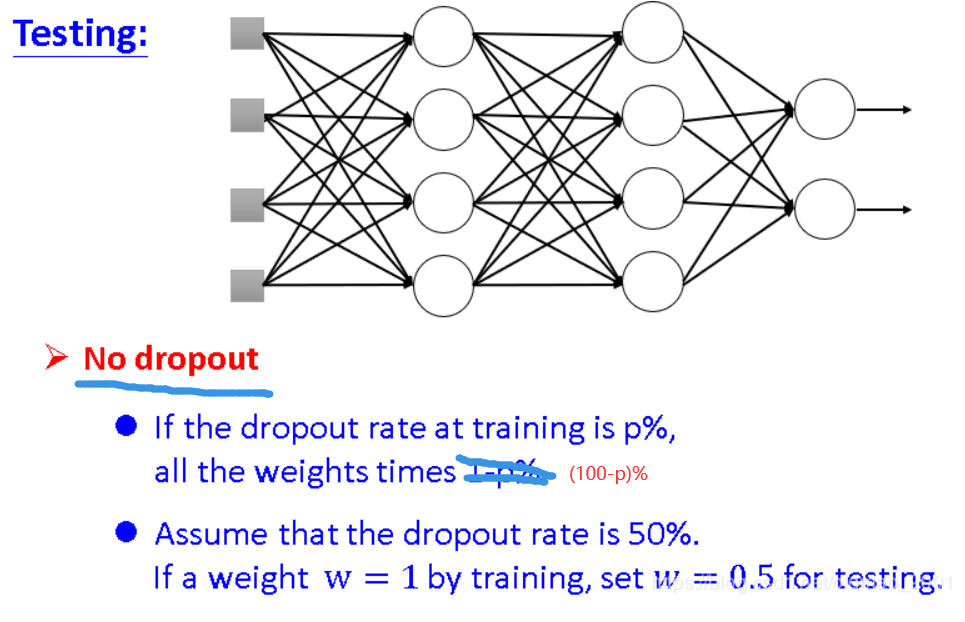
解释Dropout

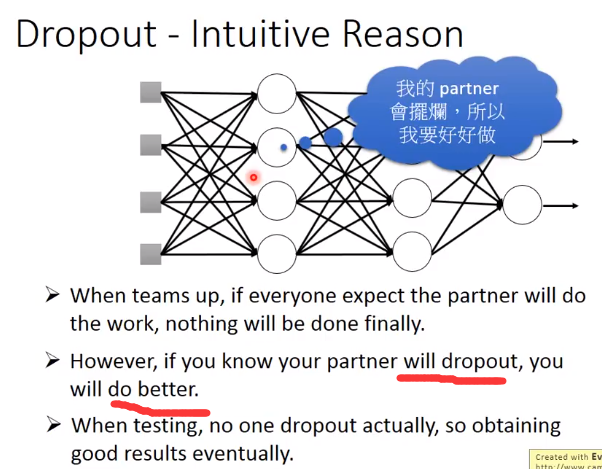
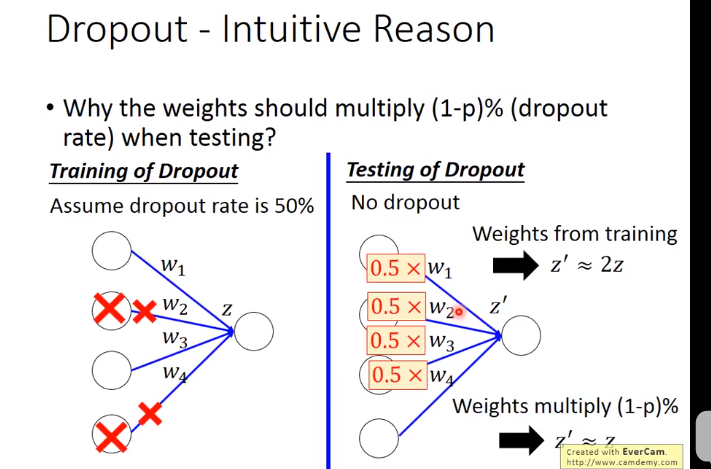
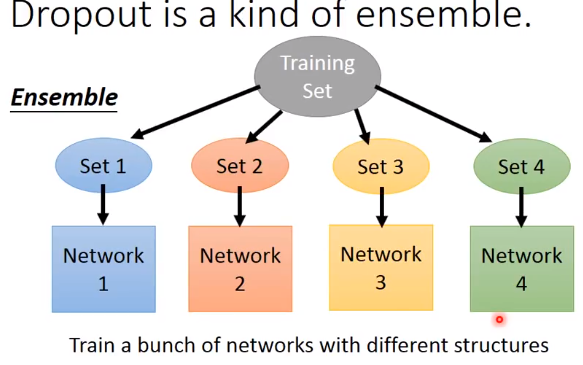
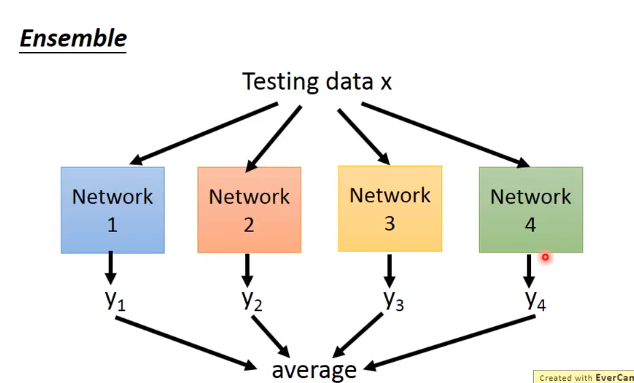
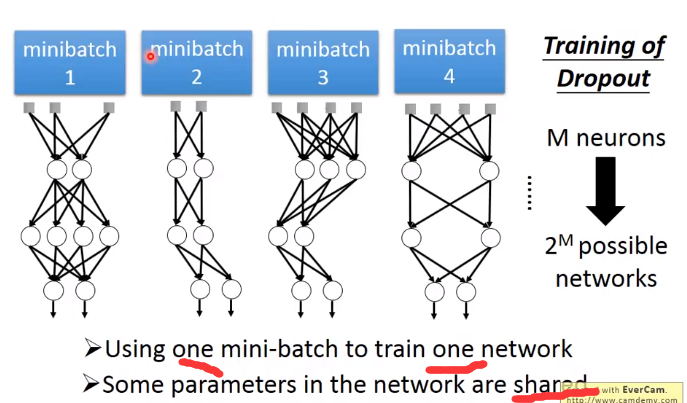
下面举个例子来解释dropout

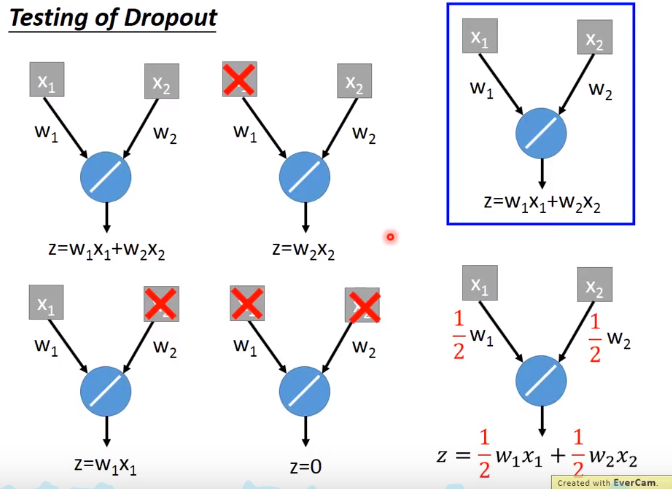
左边=(w1x1+w2x2+w2x2+w1x2+0)/4=(w1x1+w2x2)/2=右边
这里等于关系是因为激活函数是线性函数（ReLU，Maxout的时候dropout比较好用），如果是sigmoid函数就变成约等于