Codeforces Add on a Tree
1 second
256 megabytes
standard input
standard output
Note that this is the first problem of the two similar problems. You can hack this problem only if you solve both problems.
You are given a tree with nn nodes. In the beginning, 00 is written on all edges. In one operation, you can choose any 22 distinct leaves uu, vvand any real number xx and add xx to values written on all edges on the simple path between uu and vv.
For example, on the picture below you can see the result of applying two operations to the graph: adding 22 on the path from 77 to 66, and then adding −0.5−0.5 on the path from 44 to 55.
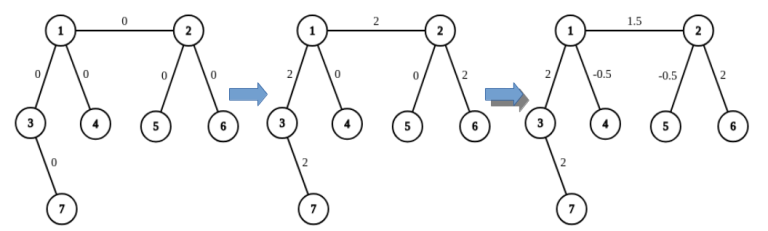
Is it true that for any configuration of real numbers written on edges, we can achieve it with a finite number of operations?
Leaf is a node of a tree of degree 11. Simple path is a path that doesn't contain any node twice.
The first line contains a single integer nn (2≤n≤1052≤n≤105) — the number of nodes.
Each of the next n−1n−1 lines contains two integers uu and vv (1≤u,v≤n1≤u,v≤n, u≠vu≠v), meaning that there is an edge between nodes uu and vv. It is guaranteed that these edges form a tree.
If there is a configuration of real numbers written on edges of the tree that we can't achieve by performing the operations, output "NO".
Otherwise, output "YES".
You can print each letter in any case (upper or lower).
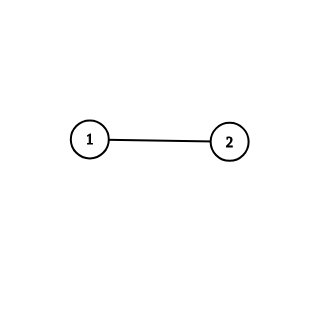
2
1 2
YES
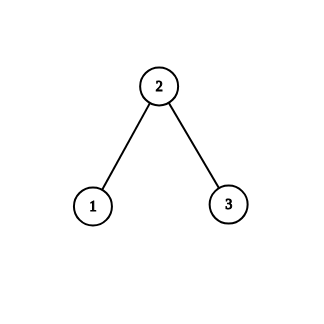
3
1 2
2 3
NO
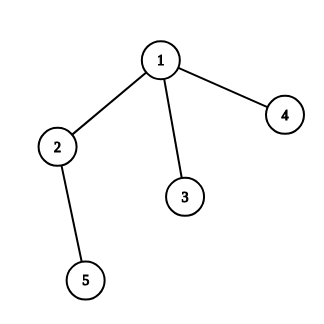
5
1 2
1 3
1 4
2 5
NO
6
1 2
1 3
1 4
2 5
2 6
YES
In the first example, we can add any real xx to the value written on the only edge (1,2)(1,2).
In the second example, one of configurations that we can't reach is 00 written on (1,2)(1,2) and 11 written on (2,3)(2,3).
Below you can see graphs from examples 33, 44:
题意:给一颗n个节点边权都为0的树,现在有一种操作可以任意选择这颗树上的两个叶子节点(度数为1的节点)使得这两个节点简单路径(没有重复节点的路径)上的边权加上一个任意实数,
问给定节点的连接关系形成一颗树,能否有限次使用上述操作使得树上的边权可以为任意实数(可能每一条边都不一样)
思路:样例2表明,如果存在一个节点恰好只连接了两个节点,则其只连了两条边,形成一条链,则条链必定会在两个根节点的简单路径上,而简单路径上的边权是同时加一个实数的,所以这个节点的两条边必定同时加一个实数且两条边的值必定相同
故这两条边无法在有限次操作内到达权值不同的情况,应输出NO,其他情况都可以通过某些边加上一些值,某些边减去一些值得到,输出YES
#include<bits/stdc++.h>
using namespace std;
const int amn=1e5+;
vector<int> a[amn];
int main(){
int n,f=,u,v;
cin>>n;
for(int i=;i<n;i++){
cin>>u>>v;
a[u].push_back(v);
a[v].push_back(u);
}
for(int i=;i<=n;i++){
if(a[i].size()==){ ///若存在一个点度数为2,则输出NO
f=;
break;
}
}
if(f)printf("YES\n"); ///否则输出YES
else printf("NO\n");
}
/***
给一颗n个节点边权都为0的树,现在有一种操作可以任意选择这颗树上的两个叶子节点(度数为1的节点)使得这两个节点简单路径(没有重复节点的路径)上的边权加上一个任意实数,
问给定节点的连接关系形成一颗树,能否有限次使用上述操作使得树上的边权可以为任意实数(可能每一条边都不一样)
样例2表明,如果存在一个节点恰好只连接了两个节点,则其只连了两条边,形成一条链,则条链必定会在两个根节点的简单路径上,而简单路径上的边权是同时加一个实数的,所以这个节点的两条边必定同时加一个实数且两条边的值必定相同
故这两条边无法在有限次操作内到达权值不同的情况,应输出NO,其他情况都可以通过某些边加上一些值,某些边减去一些值得到,输出YES
***/
Codeforces Add on a Tree的更多相关文章
- Codeforces 280C Game on tree【概率DP】
Codeforces 280C Game on tree LINK 题目大意:给你一棵树,1号节点是根,每次等概率选择没有被染黑的一个节点染黑其所有子树中的节点,问染黑所有节点的期望次数 #inclu ...
- Codeforces A. Game on Tree(期望dfs)
题目描述: Game on Tree time limit per test 1 second memory limit per test 256 megabytes input standard i ...
- Codeforces 461B Appleman and Tree(木dp)
题目链接:Codeforces 461B Appleman and Tree 题目大意:一棵树,以0节点为根节点,给定每一个节点的父亲节点,以及每一个点的颜色(0表示白色,1表示黑色),切断这棵树的k ...
- Codeforces 1129 E.Legendary Tree
Codeforces 1129 E.Legendary Tree 解题思路: 这题好厉害,我来复读一下官方题解,顺便补充几句. 首先,可以通过询问 \(n-1\) 次 \((S=\{1\},T=\{ ...
- Codeforces Round #781(C. Tree Infection)
Codeforces Round #781 C. Tree Infection time limit per test 1 second memory limit per test 256 megab ...
- Codeforces 1189D2. Add on a Tree: Revolution
传送门 首先可以证明一颗树合法的充分必要条件是不存在某个节点的度数为 $2$ 首先它是必要的,考虑任意一条边连接的两点如果存在某一点 $x$ 度数为 $2$ ,那么说明 $x$ 还有连一条边出去,那么 ...
- CodeForces 396C On Changing Tree
On Changing Tree Time Limit: 2000ms Memory Limit: 262144KB This problem will be judged on CodeForces ...
- Codeforces 734E. Anton and Tree 搜索
E. Anton and Tree time limit per test: 3 seconds memory limit per test :256 megabytes input:standard ...
- codeforces 161D Distance in Tree 树形dp
题目链接: http://codeforces.com/contest/161/problem/D D. Distance in Tree time limit per test 3 secondsm ...
随机推荐
- Linux IO多路复用
监听文件描述符的状态来进行相应的读写操作,3个函数: 123 selectpollepoll 123456789 int (int nfds, fd_set *readfds, fd_set *wri ...
- 会编程的 AI + 会修 Bug 的 AI,等于什么 ?
2017-02-25 Python开发者 (点击上方公众号,可快速关注) 关于人工智能未来的畅想,除了家庭服务机器人,快递无人机,医用机器人等等,Lucas Carlson 认为人工智能在另外一个领域 ...
- golang xml解析
第二章里还提到了xml的解析部分.之前有想整理下encoding包下常用的几个文件格式的处理.这次刚好整理下xml的部分.先上例子 1 2 3 4 5 6 7 8 9 10 11 12 13 14 1 ...
- 蚂蚁金服招聘-无线测试开发(20k-36k/月)
蚂蚁金服-支付宝国际事业部-高级测试开发工程师/测试专家 工作年限:三年以上学历要求:本科期望层级:P6/P7工作地点:上海,杭州,深圳等为什么选择加入我们? 我们的岗位有何不同?1.国际化远景:随着 ...
- mongodb 修改oplogSize
oplog是local库下的一个固定集合,Secondary就是通过查看Primary的oplog这个集合来进行复制的.每个节点都有oplog,记录从主节点复制过来的信息,这样每个成员都可以作为同步源 ...
- springboot配置文件读取pom文件信息
解决的问题 springboot(当然别的也可以)多环境切换需要该配置文件,打包时不够方便. 解决: 配置文件能读取pom文件中的配置,根据命令选择不同配置注入springboot的配置文件中 pom ...
- fsLayuiPlugin多数据表格使用
fsLayuiPlugin 是一个基于layui的快速开发插件,支持数据表格增删改查操作,提供通用的组件,通过配置html实现数据请求,减少前端js重复开发的工作. GitHub下载 码云下载 测试环 ...
- 使用MySQL练习增删改查时因为版本问题出现连接错误
使用MySQL练习增删改查时出现连接错误,错误提示如下: 2020-02-19 19:53:51.088 ERROR 16328 --- [reate-249798694] com.alibaba.d ...
- ubuntu16.04卸载docker
1.sudo apt-get remove docker-ce 2.apt-get remove -y docker-* rm -rf /var/lib/docker
- angular的开始历程
开始写angular了,抑制不住的开心,比react差点开心,vue开始太虐 喜欢一个人要不要表个白?其实也没啥资格喜欢~!!考虑一段时间吧 9.29表白了,嗯,被拒绝的干脆利落 为他写了一首小诗歌, ...
