易知大学任务（2）成绩表雷达分析图

　　　　　　（4）自定义手绘风

概述

Numpy  最基本的库，是用于处理含有同种元素的多维数组运算的第三方库

—科学计算包，python数据分析及科学计算的基础库，几乎支撑所有其他库

—支持N维数组运算、处理大型矩阵、成熟的广播函数库、矢量运算、线性代数、傅里叶变换、随机数生成等功能

—可与C++/Fortran语言无缝结合。树莓派Python v3默认安装已经包含了numpy。

本笔记包含以下内容

一、导入模块                            二、生成数组                                 三、运算函数                              四、数组与数值的运算

五、数组与数组的运算              六、转置                                        七、点积/内积                             八、数组元素访问

九、数组支持函数运算            十、改变数组大小                          十一、切片操作                          十二、布尔运算

十三、取整运算                       十四、广播                                     十五、分段函数                          十六、计算唯一值以及出现次数

十七、矩阵运算                        十八、矩阵不同维度上的计算

一、导入模块

>>> import numpy as np

二、生成数组

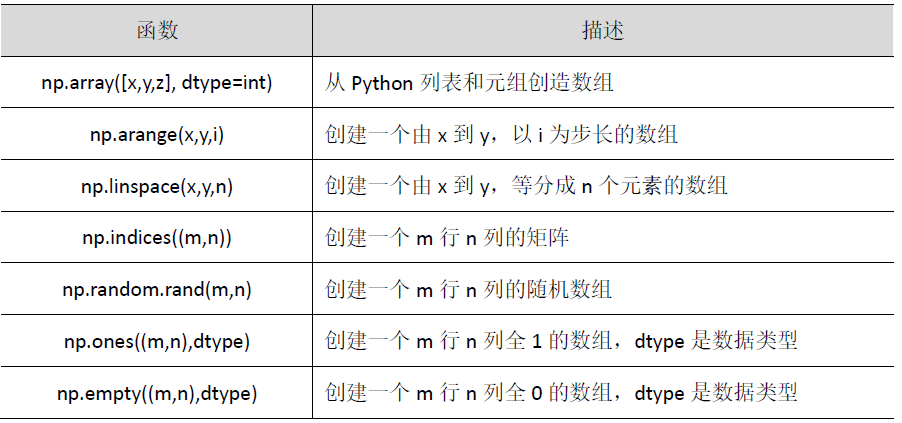
  1. >>> np.array([1, 2, 3, 4, 5])        # 把列表转换为数组
  2. array([1, 2, 3, 4, 5])
  3. >>> np.array((1, 2, 3, 4, 5))        # 把元组转换成数组
  4. array([1, 2, 3, 4, 5])
  5. >>> np.array(range(5))               # 把range对象转换成数组
  6. array([0, 1, 2, 3, 4])
  7. >>> np.array([[1, 2, 3], [4, 5, 6]]) # 二维数组
  8. array([[1, 2, 3],
  9.        [4, 5, 6]])
  10. >>> np.arange(8)                     # 类似于内置函数range()
  11. array([0, 1, 2, 3, 4, 5, 6, 7])
  12. >>> np.arange(1, 10, 2)
  13. array([1, 3, 5, 7, 9])
  14. >>> np.linspace(0, 10, 11)         # 等差数组，包含11个数
  15. array([  0.,   1.,   2.,   3.,   4.,   5.,   6.,   7.,   8.,   9.,  10.])
  16. >>> np.linspace(0, 10, 11, endpoint=False) # 不包含终点
  17. array([ 0.        ,  0.90909091,  1.81818182,  2.72727273,  3.63636364,
  18.         4.54545455,  5.45454545,  6.36363636,  7.27272727,  8.18181818,
  19.         9.09090909])
  20. >>> np.logspace(0, 100, 10)        # 对数数组
  21. array([ 1.00000000e+000,   1.29154967e+011,   1.66810054e+022,
  22.         2.15443469e+033,   2.78255940e+044,   3.59381366e+055,
  23.         4.64158883e+066,   5.99484250e+077,   7.74263683e+088,
  24.         1.00000000e+100])
  25. >>> np.logspace(1,6,5, base=2)     # 对数数组，相当于2 ** np.linspace(1,6,5)
  26. array([  2.        ,   4.75682846,  11.3137085 ,  26.90868529,  64.        ])
  27. >>> np.zeros(3)                    # 全0一维数组
  28. array([ 0.,  0.,  0.])
  29. >>> np.ones(3)                     # 全1一维数组
  30. array([ 1.,  1.,  1.])
  31. >>> np.zeros((3,3))              # 全0二维数组，3行3列
  32. [[ 0.  0.  0.]
  33.  [ 0.  0.  0.]
  34.  [ 0.  0.  0.]]
  35. >>> np.zeros((3,1))              # 全0二维数组，3行1列
  36. array([[ 0.],
  37.        [ 0.],
  38.        [ 0.]])
  39. >>> np.zeros((1,3))              # 全0二维数组，1行3列
  40. array([[ 0.,  0.,  0.]])
  41. >>> np.ones((1,3))               # 全1二维数组
  42. array([[ 1.,  1.,  1.]])
  43. >>> np.ones((3,3))               # 全1二维数组
  44. array([[ 1.,  1.,  1.],
  45.        [ 1.,  1.,  1.],
  46.        [ 1.,  1.,  1.]])
  47. >>> np.identity(3)      # 单位矩阵
  48. array([[ 1.,  0.,  0.],
  49.        [ 0.,  1.,  0.],
  50.        [ 0.,  0.,  1.]])
  51. >>> np.identity(2)
  52. array([[ 1.,  0.],
  53.        [ 0.,  1.]])
  54. >>> np.empty((3,3))     # 空数组，只申请空间而不初始化，元素值是不确定的
  55. array([[ 0.,  0.,  0.],
  56.        [ 0.,  0.,  0.],
  57.        [ 0.,  0.,  0.]])　　

三、运算函数

（1）算术运算函数

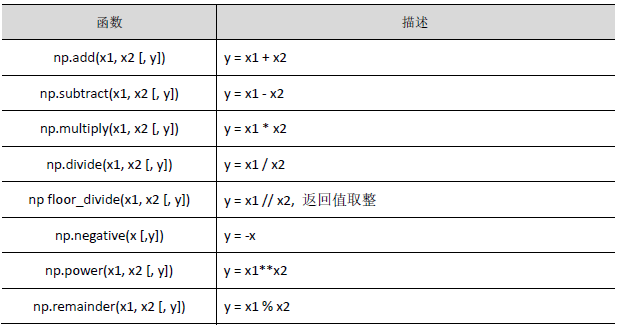
（2）比较运算函数

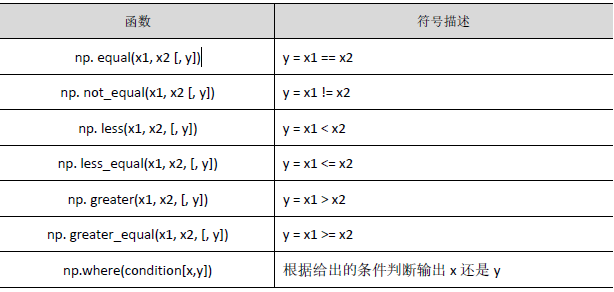
（3）其他运算函数

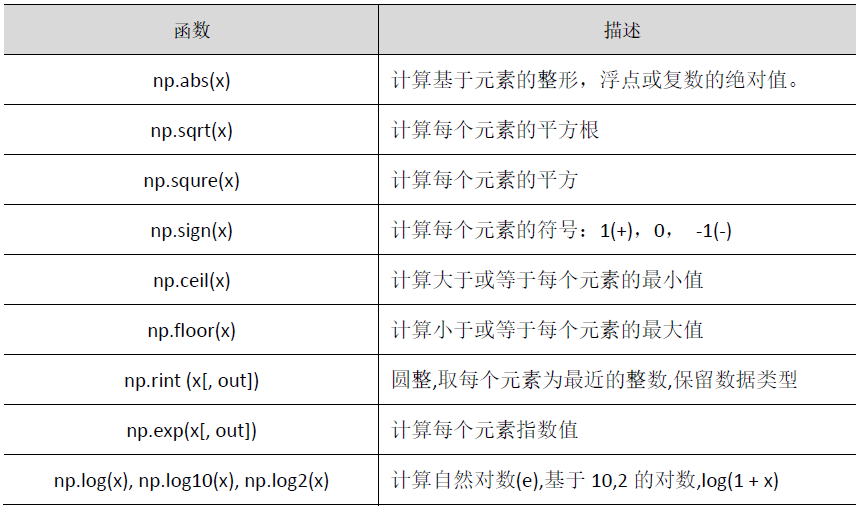
四、数组与数值的运算

  1. >>> x = np.array((1, 2, 3, 4, 5))    # 创建数组对象
  2. >>> x
  3. array([1, 2, 3, 4, 5])
  4. >>> x * 2                            # 数组与数值相乘，返回新数组
  5. array([ 2, 4, 6, 8, 10])
  6. >>> x / 2                            # 数组与数值相除
  7. array([ 0.5, 1. , 1.5, 2. , 2.5])
  8. >>> x // 2                           # 数组与数值整除
  9. array([0, 1, 1, 2, 2], dtype=int32)
  10. >>> x ** 3                           # 幂运算
  11. array([1, 8, 27, 64, 125], dtype=int32)
  12. >>> x + 2                            # 数组与数值相加
  13. array([3, 4, 5, 6, 7])
  14. >>> x % 3                            # 余数
  15. array([1, 2, 0, 1, 2], dtype=int32)
  16. >>> 2 ** x
  17. array([2, 4, 8, 16, 32], dtype=int32)
  18. >>> 2 / x
  19. array([2. ,1. ,0.66666667, 0.5, 0.4])
  20. >>> 63 // x
  21. array([63, 31, 21, 15, 12], dtype=int32)　

五、数组与数组的运算

  1. >>> a = np.array((1, 2, 3))
  2. >>> b = np.array(([1, 2, 3], [4, 5, 6], [7, 8, 9]))
  3. >>> c = a * b                      # 数组与数组相乘
  4. >>> c                              # a中的每个元素乘以b中的对应列元素
  5. array([[ 1, 4, 9],
  6.        [ 4, 10, 18],
  7.        [ 7, 16, 27]])
  8. >>> c / b     #np.devide(,)        # 数组之间的除法运算
  9. array([[ 1.,  2.,  3.],
  10.        [ 1.,  2.,  3.],
  11.        [ 1.,  2.,  3.]])
  12. >>> c / a
  13. array([[ 1.,  2.,  3.],
  14.        [ 4.,  5.,  6.],
  15.        [ 7.,  8.,  9.]])
  16. >>> a + a          #np.add(,)              # 数组之间的加法运算
  17. array([2, 4, 6])
  18. >>> a * a                                  # 数组之间的乘法运算
  19. array([1, 4, 9])
  20. >>> a - a                                  # 数组之间的减法运算
  21. array([0, 0, 0])
  22. >>> a / a                                  # 数组之间的除法运算
  23. array([ 1., 1., 1.])

六、转置　

  1. >>> b = np.array(([1, 2, 3], [4, 5, 6], [7, 8, 9]))
  2. >>> b
  3. array([[1, 2, 3],
  4.        [4, 5, 6],
  5.        [7, 8, 9]])
  6. >>> b.T                           # 转置
  7. array([[1, 4, 7],
  8.        [2, 5, 8],
  9.        [3, 6, 9]])
  10. >>> a = np.array((1, 2, 3, 4))
  11. >>> a
  12. array([1, 2, 3, 4])
  13. >>> a.T                           # 一维数组转置以后和原来是一样的
  14. array([1, 2, 3, 4])

七、点积/内积

  1. >>> a = np.array((5, 6, 7))
  2. >>> b = np.array((6, 6, 6))
  3. >>> a.dot(b)                                # 向量内积
  4. 108
  5. >>> np.dot(a,b)
  6. 108
  7. >>> c = np.array(([1,2,3],[4,5,6],[7,8,9])) # 二维数组
  8. >>> c.dot(a)                                # 二维数组的每行与一维向量计算内积
  9. array([ 38, 92, 146])
  10. >>> a.dot(c)                                # 一维向量与二维向量的每列计算内积
  11. array([78, 96, 114])

八、数组元素访问

  1. >>> b = np.array(([1,2,3],[4,5,6],[7,8,9]))
  2. >>> b
  3. array([[1, 2, 3],
  4.        [4, 5, 6],
  5.        [7, 8, 9]])
  6. >>> b[0]              # 第0行
  7. array([1, 2, 3])
  8. >>> b[0][0]           # 第0行第0列的元素值
  9. 1
  10. >>> b[0,2]            # 第0行第2列的元素值
  11. 3
  12. >>> b[[0,1]]          # 第0行和第1行
  13. array([[1, 2, 3],
  14.        [4, 5, 6]])
  15. >>> b[[0,1], [1,2]]   #第0行第1列的元素和第1行第2列的元素
  16. array([2, 6])
  17. >>> x = np.arange(0,100,10,dtype=np.floating)
  18. >>> x
  19. array([  0.,  10.,  20.,  30.,  40.,  50.,  60.,  70.,  80.,  90.])
  20. >>> x[[1, 3, 5]]                 # 同时访问多个位置上的元素
  21. array([ 10.,  30.,  50.])
  22. >>> x[[1, 3, 5]] = 3             # 把多个位置上的元素改为相同的值
  23. >>> x
  24. array([  0.,   3.,  20.,   3.,  40.,   3.,  60.,  70.,  80.,  90.])
  25. >>> x[[1, 3, 5]] = [34, 45, 56]  # 把多个位置上的元素改为不同的值
  26. >>> x
  27. array([  0.,  34.,  20.,  45.,  40.,  56.,  60.,  70.,  80.,  90.])

九、数组支持函数运算

  1. >>> x = np.arange(0, 100, 10, dtype=np.floating)
  2. >>> np.sin(x)                             # 一维数组中所有元素求正弦值
  3. array([ 0.        , -0.54402111,  0.91294525, -0.98803162,  0.74511316,
  4.       -0.26237485, -0.30481062,  0.77389068, -0.99388865,  0.89399666])
  5. >>> b = np.array(([1, 2, 3], [4, 5, 6], [7, 8, 9]))
  6. >>> np.cos(b)                             # 二维数组中所有元素求余弦值
  7. array([[ 0.54030231, -0.41614684, -0.9899925 ],
  8.        [-0.65364362,  0.28366219,  0.96017029],
  9.        [ 0.75390225, -0.14550003, -0.91113026]])
  10. >>> np.round(_)                           # 四舍五入
  11. array([[ 1., -0., -1.],
  12.        [-1.,  0.,  1.],
  13.        [ 1., -0., -1.]])
  14. >>> x = np.random.rand(10) * 10            # 包含10个随机数的数组
  15. >>> x
  16. array([ 2.16124573,  2.58272611,  6.18827437,  5.21282916,  4.06596404,
  17.         3.34858432,  5.60654631,  9.49699461,  1.68564166,  2.9930861 ])
  18. >>> np.floor(x)                            # 所有元素向下取整
  19. array([ 2.,  2.,  6.,  5.,  4.,  3.,  5.,  9.,  1.,  2.])
  20. >>> np.ceil(x)                             # 所有元素向上取整
  21. array([  3.,   3.,   7.,   6.,   5.,   4.,   6.,  10.,   2.,   3.])

十、改变数组大小

  1. >>> a = np.arange(1, 11, 1)
  2. >>> a
  3. array([1, 2, 3, 4, 5, 6, 7, 8, 9, 10])
  4. >>> a.shape = 2, 5                         # 改为2行5列
  5. >>> a
  6. array([[ 1,  2,  3,  4,  5],
  7.        [ 6,  7,  8,  9, 10]])
  8. >>> a.shape = 5, -1                        # -1表示自动计算，原地修改
  9. >>> a
  10. array([[ 1,  2],
  11.        [ 3,  4],
  12.        [ 5,  6],
  13.        [ 7,  8],
  14.        [ 9, 10]])
  15. >>> b = a.reshape(2,5)                     # reshape()方法返回新数组
  16. >>> b
  17. array([[ 1,  2,  3,  4,  5],
  18.        [ 6,  7,  8,  9, 10]])

十一、切片操作

  1. >>> a = np.arange(10)
  2. >>> a
  3. array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])
  4. >>> a[::-1]                           # 反向切片
  5. array([9, 8, 7, 6, 5, 4, 3, 2, 1, 0])
  6. >>> a[::2]                            # 隔一个取一个元素
  7. array([0, 2, 4, 6, 8])
  8. >>> a[:5]                             # 前5个元素
  9. array([0, 1, 2, 3, 4])
  10. >>> c = np.arange(25)     # 创建数组
  11. >>> c.shape = 5,5         # 修改数组大小
  12. >>> c
  13. array([[ 0,  1,  2,  3,  4],
  14.        [ 5,  6,  7,  8,  9],
  15.        [10, 11, 12, 13, 14],
  16.        [15, 16, 17, 18, 19],
  17.        [20, 21, 22, 23, 24]])
  18. >>> c[0, 2:5]             # 第0行中下标[2,5)之间的元素值
  19. array([2, 3, 4])
  20. >>> c[1]                  # 第0行所有元素
  21. array([5, 6, 7, 8, 9])
  22. >>> c[2:5, 2:5]           # 行下标和列下标都介于[2,5)之间的元素值
  23. array([[12, 13, 14],
  24.        [17, 18, 19],
  25.        [22, 23, 24]])

十二、布尔运算　　

  1. >>> x = np.random.rand(10) # 包含10个随机数的数组
  2. >>> x
  3. array([ 0.56707504,  0.07527513,  0.0149213 ,  0.49157657,  0.75404095,
  4.       0.40330683,  0.90158037,  0.36465894,  0.37620859,  0.62250594])
  5. >>> x > 0.5               # 比较数组中每个元素值是否大于0.5
  6. array([ True, False, False, False,  True, False,  True, False, False,  True], dtype=bool)
  7. >>> x[x>0.5]              # 获取数组中大于0.5的元素，可用于检测和过滤异常值
  8. array([ 0.56707504,  0.75404095,  0.90158037,  0.62250594])
  9. >>> x < 0.5
  10. array([False,  True,  True,  True, False,  True, False,  True,  True, False], dtype=bool)
  11. >>> np.all(x<1)           # 测试是否全部元素都小于1
  12. True
  13. >>> np.any([1,2,3,4])         # 是否存在等价于True的元素
  14. True
  15. >>> np.any([0])
  16. False
  17. >>> a = np.array([1, 2, 3])
  18. >>> b = np.array([3, 2, 1])
  19. >>> a > b                     # 两个数组中对应位置上的元素比较
  20. array([False, False,  True], dtype=bool)
  21. >>> a[a>b]
  22. array([3])
  23. >>> a == b
  24. array([False,  True, False], dtype=bool)
  25. >>> a[a==b]
  26. array([2])

十三、取整运算　　　

  1. >>> x = np.random.rand(10)*50      # 10个随机数
  2. >>> x
  3. array([ 43.85639765,  30.47354735,  43.68965984,  38.92963767,
  4.          9.20056878,  21.34765863,   4.61037809,  17.99941701,
  5.         19.70232038,  30.05059154])
  6. >>> np.int64(x)                    # 取整
  7. array([43, 30, 43, 38,  9, 21,  4, 17, 19, 30], dtype=int64)
  8. >>> np.int32(x)
  9. array([43, 30, 43, 38,  9, 21,  4, 17, 19, 30])
  10. >>> np.int16(x)
  11. array([43, 30, 43, 38,  9, 21,  4, 17, 19, 30], dtype=int16)
  12. >>> np.int8(x)
  13. array([43, 30, 43, 38,  9, 21,  4, 17, 19, 30], dtype=int8)

十四、广播

  1. >>> a = np.arange(0,60,10).reshape(-1,1)     # 列向量
  2. >>> b = np.arange(0,6)                       # 行向量
  3. >>> a
  4. array([[ 0],
  5.        [10],
  6.        [20],
  7.        [30],
  8.        [40],
  9.        [50]])
  10. >>> b
  11. array([0, 1, 2, 3, 4, 5])
  12. >>> a[0] + b                                 # 数组与标量的加法
  13. array([0, 1, 2, 3, 4, 5])
  14. >>> a[1] + b
  15. array([10, 11, 12, 13, 14, 15])
  16. >>> a + b                                     # 广播
  17. array([[ 0,  1,  2,  3,  4,  5],
  18.        [10, 11, 12, 13, 14, 15],
  19.        [20, 21, 22, 23, 24, 25],
  20.        [30, 31, 32, 33, 34, 35],
  21.        [40, 41, 42, 43, 44, 45],
  22.        [50, 51, 52, 53, 54, 55]])
  23. >>> a * b
  24. array([[  0,   0,   0,   0,   0,   0],
  25.        [  0,  10,  20,  30,  40,  50],
  26.        [  0,  20,  40,  60,  80, 100],
  27.        [  0,  30,  60,  90,  120, 150],
  28.        [  0,  40,  80,  120, 160, 200],
  29.        [  0,  50,  100, 150,  200, 250]])

十五、分段函数

  1. >>> x = np.random.randint(0, 10, size=(1,10))
  2. >>> x
  3. array([[0, 4, 3, 3, 8, 4, 7, 3, 1, 7]])
  4. >>> np.where(x<5, 0, 1)            # 小于5的元素值对应0，其他对应1
  5. array([[0, 0, 0, 0, 1, 0, 1, 0, 0, 1]])
  6. >>> np.piecewise(x, [x<4, x>7], [lambda x:x*2, lambda x:x*3])
  7.                                    # 小于4的元素乘以2
  8.                                    # 大于7的元素乘以3
  9.                                    # 其他元素变为0
  10. array([[ 0,  0,  6,  6, 24,  0,  0,  6,  2,  0]])

十六、计算唯一值以及出现次数

  1. >>> x = np.random.randint(0, 10, 7)
  2. >>> x
  3. array([8, 7, 7, 5, 3, 8, 0])
  4. >>> np.bincount(x)   # 元素出现次数，0出现1次，
  5.                      # 1、2没出现，3出现1次，以此类推
  6. array([1, 0, 0, 1, 0, 1, 0, 2, 2], dtype=int64)
  7. >>> np.sum(_)        # 所有元素出现次数之和等于数组长度
  8. 7
  9. >>> np.unique(x)     # 返回唯一元素值
  10. array([0, 3, 5, 7, 8])

十七、矩阵运算

  1. >>> a_list = [3, 5, 7]
  2. >>> a_mat = np.matrix(a_list)            # 创建矩阵
  3. >>> a_mat
  4. matrix([[3, 5, 7]])
  5. >>> a_mat.T                              # 矩阵转置
  6. matrix([[3],
  7.         [5],
  8.         [7]])
  9. >>> a_mat.shape                          # 矩阵形状
  10. (1, 3)
  11. >>> a_mat.size                           # 元素个数
  12. 3
  13. >>> a_mat.mean()                         # 元素平均值
  14. 5.0
  15. >>> a_mat.sum()                          # 所有元素之和
  16. 15
  17. >>> a_mat.max()                          # 最大值
  18. 7
  19. >>> a_mat.max(axis=1)                    # 横向最大值
  20. matrix([[7]])
  21. >>> a_mat.max(axis=0)                    # 纵向最大值
  22. matrix([[3, 5, 7]])
  23. >>> b_mat = np.matrix((1, 2, 3))         # 创建矩阵
  24. >>> b_mat
  25. matrix([[1, 2, 3]])
  26. >>> a_mat * b_mat.T                      # 矩阵相乘
  27. matrix([[34]])
  28. >>> c_mat = np.matrix([[1, 5, 3], [2, 9, 6]]) # 创建二维矩阵
  29. >>> c_mat
  30. matrix([[1, 5, 3],
  31.         [2, 9, 6]])
  32. >>> c_mat.argsort(axis=0)                     # 纵向排序后的元素序号
  33. matrix([[0, 0, 0],
  34.         [1, 1, 1]], dtype=int64)
  35. >>> c_mat.argsort(axis=1)                     # 横向排序后的元素序号
  36. matrix([[0, 2, 1],
  37.         [0, 2, 1]], dtype=int64)
  38. >>> d_mat = np.matrix([[1, 2, 3], [4, 5, 6], [7, 8, 9]])
  39. >>> d_mat.diagonal()                          # 矩阵对角线元素
  40. matrix([[1, 5, 9]])

十八、矩阵不同维度上的计算

  1. >>> x = np.matrix(np.arange(0,10).reshape(2,5))  # 二维矩阵
  2. >>> x
  3. matrix([[0, 1, 2, 3, 4],
  4.         [5, 6, 7, 8, 9]])
  5. >>> x.sum()                                      # 所有元素之和
  6. 45
  7. >>> x.sum(axis=0)                                # 纵向求和
  8. matrix([[ 5,  7,  9, 11, 13]])
  9. >>> x.sum(axis=1)                                # 横向求和
  10. matrix([[10],
  11.         [35]])
  12. >>> x.mean()                                     # 平均值
  13. 4.5
  14. >>> x.mean(axis=1)
  15. matrix([[ 2.],
  16.         [ 7.]])
  17. >>> x.mean(axis=0)
  18. matrix([[ 2.5,  3.5,  4.5,  5.5,  6.5]])
  19. >>> x.max()                                # 所有元素最大值
  20. 9
  21. >>> x.max(axis=0)                          # 纵向最大值
  22. matrix([[5, 6, 7, 8, 9]])
  23. >>> x.max(axis=1)                          # 横向最大值
  24. matrix([[4],
  25.         [9]])
  26. >>> weight = [0.3, 0.7]                    # 权重
  27. >>> np.average(x, axis=0, weights=weight)
  28. matrix([[ 3.5,  4.5,  5.5,  6.5,  7.5]])
  29. >>> x = np.matrix(np.random.randint(0, 10, size=(3,3)))
  30. >>> x
  31. matrix([[3, 7, 4],
  32.         [5, 1, 8],
  33.         [2, 7, 0]])
  34. >>> x.std()                         # 标准差
  35. 2.6851213274654606
  36. >>> x.std(axis=1)                   # 横向标准差
  37. matrix([[ 1.69967317],
  38.         [ 2.86744176],
  39.         [ 2.94392029]])
  40. >>> x.std(axis=0)                   # 纵向标准差
  41. matrix([[ 1.24721913,  2.82842712,  3.26598632]])
  42. >>> x.var(axis=0)                   # 纵向方差
  43. matrix([[  1.55555556,   8.        ,  10.66666667]])

　　

　　

　

　

　　

　

Python第三方库之Numpy库的更多相关文章

  1. 用python的matplotlib和numpy库绘制股票K线均线和成交量的整合效果（含量化验证交易策略代码）

    在用python的matplotlib和numpy库绘制股票K线均线的整合效果(含从网络接口爬取数据和验证交易策略代码)一文里,我讲述了通过爬虫接口得到股票数据并绘制出K线均线图形的方式,在本文里,将 ...

  2. Python图像处理丨OpenCV+Numpy库读取与修改像素

    摘要:本篇文章主要讲解 OpenCV+Numpy 图像处理基础知识,包括读取像素和修改像素. 本文分享自华为云社区<[Python图像处理] 二.OpenCV+Numpy库读取与修改像素> ...

  3. 利用matplotlib库和numpy库画数学图形

    首先,电脑要安装到matplotlib库和numpy库,这可以通过到命令符那里输入“pip install matplotlib ”,两个操作一样 其次,参照下列代码: import numpy as ...

  4. Python第三方常用工具、库、框架等

    Python ImagingLibrary(PIL):它提供强大的图形处理的能力,并提供广泛的图形文件格式支持,该库能进行图形格式的转换.打印和显示.还能进行一些图形效果的处理,如图形的放大.缩小和旋 ...

  5. $python数据分析基础——初识numpy库

    numpy库是python的一个著名的科学计算库,本文是一个quickstart. 引入:计算BMI BMI = 体重(kg)/身高(m)^2 假如有如下几组体重和身高数据,让求每组数据的BMI值: ...

  6. 【python】详解numpy库与pandas库axis=0，axis= 1轴的用法

    对数据进行操作时,经常需要在横轴方向或者数轴方向对数据进行操作,这时需要设定参数axis的值: axis = 0 代表对横轴操作,也就是第0轴: axis = 1 代表对纵轴操作,也就是第1轴: nu ...

  7. 用python的matplotlib和numpy库绘制股票K线均线的整合效果（含从网络接口爬取数据和验证交易策略代码）

    本人最近在尝试着发表“以股票案例入门Python编程语言”系列的文章,在这些文章里,将用Python工具绘制各种股票指标,在讲述各股票指标的含义以及计算方式的同时,验证基于各种指标的交易策略,本文是第 ...

  8. Python 学习笔记之 Numpy 库——文件操作

    1. 读写 txt 文件 a = list(range(0, 100)) a = np.array(a) # a.dtype = np.int64 np.savetxt("filename. ...

  9. Python 学习笔记之 Numpy 库——数组基础

    1. 初识数组 import numpy as np a = np.arange(15) a = a.reshape(3, 5) print(a.ndim, a.shape, a.dtype, a.s ...

随机推荐

  1. 采用TuesPechkin生成Pdf

    1.需求 前段时间有个需求,要求把网页生成pdf,找了各种插件,才决定使用这个TuesPechkin,这个是后台采用C#代码进行生成 2.做法 我要做的是一个比较简单的页面,采用MVC绑定,数据动态加 ...

  2. spark error Caused by: java.io.NotSerializableException: org.apache.hadoop.hdfs.DistributedFileSystem

    序列化问题多事rdd遍历过程中使用了没有序列化的对象. 1.将未序列化的变量定义到rdd遍历内部.如定义入数据库连接池. 2.常量定义里包含了未序列化对象 ,提出去吧 如下常量要放到main里,不能放 ...

  3. hive常用函数一

    Hive概念 Hive最适合于数据仓库应用程序,使用该应用程序进行相关静态数据分析,不需要快速响应出结果,而数据本身不会发生频繁变化. Hdfs分布式文件系统限制了hive,使其不支持记录级别的更新. ...

  4. Byte字节

    字节(Byte )是计算机信息技术用于计量存储容量的一种计量单位,作为一个单位来处理的一个二进制数字串,是构成信息的一个小单位.最常用的字节是八位的字节,即它包含八位的二进制数. 中文名 字节 外文名 ...

  5. 数据结构和算法(Golang实现)(15)常见数据结构-列表

    列表 一.列表 List 我们又经常听到列表 List数据结构,其实这只是更宏观的统称,表示存放数据的队列. 列表List:存放数据,数据按顺序排列,可以依次入队和出队,有序号关系,可以取出某序号的数 ...

  6. 文件上传——客户端检测绕过(JavaScript检测）(一）

    前言 通常再一个web程序中,一般会存在登陆注册功能,登陆后一般会有上传头像等功能,如果上传验证不严格就可能造成攻击者直接上传木马,进而控制整个web业务控制权.下面通过实例,如果程序只进行了客户端J ...

  7. AJ学IOS（36）UI之手势事件旋转_缩放_拖拽

    AJ分享,必须精品 效果 完成一个图片的捏合缩放,拖拽,旋转动作. 设计思路 拖拽: 首先是最简单的拖拽 //拖拽 -(void)panTest { UIPanGestureRecognizer *p ...

  8. JAVA—HashMap

    一些关于hashmap的学习笔记 1.HashMap底层实现原理 在JDK1.7中HashMap是以数组加链表的形式组成的,在JDK1.8之后新增了红黑树的组成结构,当链表大于8并且容量大于64时,链 ...

  9. 常用App用户体验找茬

    冯晓云: 哔哩哔哩手机客户端:视频播放只允许横屏全屏:还有长视频的“5分钟诅咒”,遇到网速不好的时候是个大写的悲剧: 必应词典UWP版本:主页新闻链接跳转后,一些页面不支持划词取译,当然本身各个页面也 ...

  10. niuke --abc

    链接:https://ac.nowcoder.com/acm/contest/1083/A来源:牛客网 给出一个字符串s,你需要做的是统计s中子串”abc”的个数.子串的定义就是存在任意下标a< ...