树的三种DFS策略(前序、中序、后序)遍历

之前刷leetcode的时候，知道求排列组合都需要深度优先搜索(DFS), 那么前序、中序、后序遍历是什么鬼，一直傻傻的分不清楚。直到后来才知道，原来它们只是DFS的三种不同策略。

N = Node(节点)

L = Left(左节点)

R = Right(右节点)

在深度优先搜索的时候，以Node的访问顺序，定义了三种不同的搜索策略：

前序遍历：结点 —> 左子树 —> 右子树

中序遍历：左子树—> 结点 —> 右子树

后序遍历：左子树 —> 右子树 —> 结点

##前序遍历

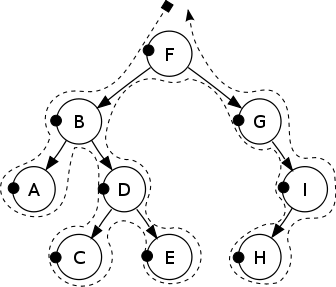
Pre-order: F, B, A, D, C, E, G, I, H.

##中序遍历

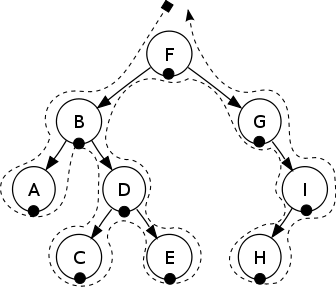
In-order: A, B, C, D, E, F, G, H, I.

在二叉搜索树(BST)中，中序遍历返回递增的一个序列

##后序遍历

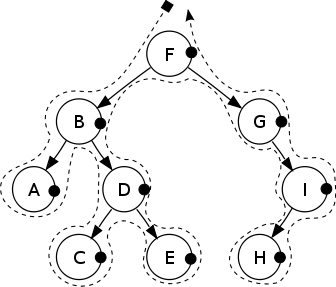
Post-order: A, C, E, D, B, H, I, G, F.

##递归代码

递归实现比较直观容易，通常DFS遍历，都需要传递一个参数 or 设置一个全局变量，来保存结果

def pre_order(self, node, results):
    if node is None:
        return
    results.append(node.val)
    self.pre_order(node.left, results)
    self.pre_order(node.right, results)

def in_order(self, node, results):
    if node is None:
        return
    self.in_order(node.left, results)
    results.append(node.val)
    self.in_order(node.right, results)

def post_order(self, node, results):
    if node is None:
        return
    self.post_order(node.left, results)
    self.post_order(node.right, results)
    results.append(node. 大专栏  树的三种DFS策略(前序、中序、后序)遍历val)

##非递归代码

深度优先遍历的非递归代码，一定用到的是stack数据接口

非递归实现前序和中序还可以，后续遍历就非常烧脑了

前序最简单，相当于for循环所有children，所以一版非递归DFS，就用前序就好了。

中序遍历，由于对于BST有一个递增的特性，所以还是比较常用的

def preorderTraversal(self, root):
    results = []
    if root is None:
        return results
    stack = [root]
    while(len(stack) > 0):
        node = stack.pop()
        results.append(node.val)
        # right first so left pop fisrt
        if node.right is not None:
            stack.append(node.right)
        if node.left is not None:
            stack.append(node.left)
    return results

def inorderTraversal(self, root):
    results = []
    if root is None:
        return results
    stack = []
    node = root
    while(len(stack) > 0 or node is not None):
        if (node is not None):
            stack.append(node)
            node = node.left
        else:
            node = stack.pop()
            results.append(node.val)
            node = node.right
    return results

def postorderTraversal(self, root):
    results = []
    if root is None:
        return results
    node = root
    stack = []
    lastNodeVisted = None
    while(len(stack) > 0 or node is not None):
        if node is not None:
            stack.append(node)
            node = node.left
        else:
            peek = stack[-1] # last element
            if (peek.right is not None and lastNodeVisted != peek.right):
                node = peek.right
            else:
                results.append(peek.val)
                lastNodeVisted = stack.pop()
    return results

–END–