GAN网络从入门教程（二）之GAN原理

在一篇博客GAN网络从入门教程（一）之GAN网络介绍中，简单的对GAN网络进行了一些介绍，介绍了其是什么，然后大概的流程是什么。

在这篇博客中，主要是介绍其数学公式，以及其算法流程。当然数学公式只是简单的介绍，并不会设计很复杂的公式推导。如果想详细的了解GAN网络的原理，推荐去看李宏毅老师的课程。B站和Youtube上面都有。

概率分布

生成器

首先我们是可以知道真实图片的分布函数$p_{data}(x)$，同时我们把假的图片也看成一个概率分布，称之为$p_g = (x,\theta)$。那么我们的目标是什么呢？我们的目标就是使得$p_g(x,\theta)$尽量的去逼近$p_{data}(x)$。在GAN中，我们使用神经网络去逼近$p_g = (x,\theta)$。

在生成器中，我们有如下模型：

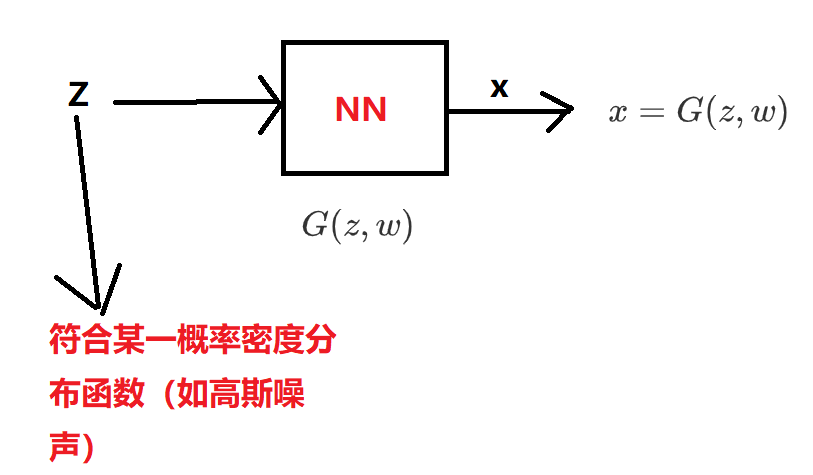
其中$z \sim P_{z}(z)$，因此$G(z)$也是一个针对于$z$概率密度分布函数。

判别器

针对于判别器，我们有$D(x,\theta)$，其代表某一张z图片$x$为真的概率。

目标函数

在Generative Adversarial Nets论文中给出了以下的目标函数，也就是GAN网络需要优化的东西。

\[\begin{equation}\min _{G} \max _{D} V(D, G)=\mathbb{E}_{\boldsymbol{x} \sim p_{\text {data }}(\boldsymbol{x})}[\log D(\boldsymbol{x})]+\mathbb{E}_{\boldsymbol{z} \sim p_{\boldsymbol{z}}(\boldsymbol{z})}[\log (1-D(G(\boldsymbol{z})))]\end{equation}
\]

公式看起来很复杂，但是我们分开来看还是比较简单的。

$D^*$

$D$网络的目标是什么？能够辨别真假，也就是说，给定一张真的图片$x$，$D$网络能够给出一个高分，也就是$D(x)$尽量大一点。而针对于生成器$G$生成的图片$G(z)$，我们希望判别器$D$尽量给低分，也就是$D(G(z))$尽量的小一点。因此$D$网络的目标函数如下所示：

\[\begin{equation}\max _{D} V(D, G)=\mathbb{E}_{\boldsymbol{x} \sim p_{\text {data }}(\boldsymbol{x})}[\log D(\boldsymbol{x})]+\mathbb{E}_{\boldsymbol{z} \sim p_{\boldsymbol{z}}(\boldsymbol{z})}[\log (1-D(G(\boldsymbol{z})))]\end{equation}
\]

在目标函数中，$x$代表的是真实数据（也就是真的图片），$G(z)$代表的是生成器生成的图片。

$G^*$

$G$网络的目标就是使得$D(G(z))$尽量得高分，因此其目标函数可以写成：

\[\begin{equation}\max _{G} V(D, G)=\mathbb{E}_{\boldsymbol{z} \sim p_{\boldsymbol{z}}(\boldsymbol{z})}[\log (D(G(\boldsymbol{z})))]\end{equation}
\]

$D(G(z))$尽量得高分（分数在$[0,1]$之间），等价于$1 - D(G(z))$尽量的低分，因此，上述目标函数等价于：

\[\begin{equation}\min _{G} V(D, G)=\mathbb{E}_{\boldsymbol{z} \sim p_{\boldsymbol{z}}(\boldsymbol{z})}[\log (1-D(G(\boldsymbol{z})))]\end{equation}
\]

因此我们优化$D^*$和优化$G^*$结合起来，也就是变成了论文中的目标函数：

证明存在全局最优解

上面的公式看起来很合理，但是如果不存在最优解的话，一切也都是无用功。

D最优解

首先，我们固定G，来优化D，目标函数为：

$\begin{equation} V(G, D)=\mathbb{E}_{\boldsymbol{x} \sim p_{\text {data }}(\boldsymbol{x})}[\log D(\boldsymbol{x})]+\mathbb{E}_{\boldsymbol{z} \sim p_{\boldsymbol{z}}(\boldsymbol{z})}[\log (1-D(G(\boldsymbol{z})))]\end{equation}$

我们可以写做：

\[\begin{equation}\begin{aligned}
V(G, D) &=\int_{\boldsymbol{x}} p_{\text {data }}(\boldsymbol{x}) \log (D(\boldsymbol{x})) d x+\int_{\boldsymbol{z}} p_{\boldsymbol{z}}(\boldsymbol{z}) \log (1-D(g(\boldsymbol{z}))) d z \\
&=\int_{\boldsymbol{x}} [ p_{\text {data }}(\boldsymbol{x}) \log (D(\boldsymbol{x}))+p_{g}(\boldsymbol{x}) \log (1-D(\boldsymbol{x}))] d x
\end{aligned}\end{equation}
\]

我们设（$D$代表$D(x)$，可以代表任何函数）：

\[f(D) = P_{data}(x) log D + P_G(x)log(1-D)
\]

对于每一个固定的$x$而言，为了使$V$最大，我们当然是希望$f(D)$越大越好，这样积分后的值也就越大。因为固定了$G$，因此$p_g(x)$是固定的，而$P_{data}$是客观存在的，则值也是固定的。我们对$f(D)$求导，然后令$f'(D) = 0$，可得：

\[\begin{equation}D^{*}=\frac{P_{d a t a}(x)}{P_{d a t a}(x)+P_{G}(x)}\end{equation}
\]

下图表示了，给定三个不同的 $G1，G3，G3$ 分别求得的令 $V(G,D)$最大的那个$ D^∗$，横轴代表了$P_{data}$，蓝色曲线代表了可能的 $P_G$，绿色的距离代表了 $V(G,D)$：

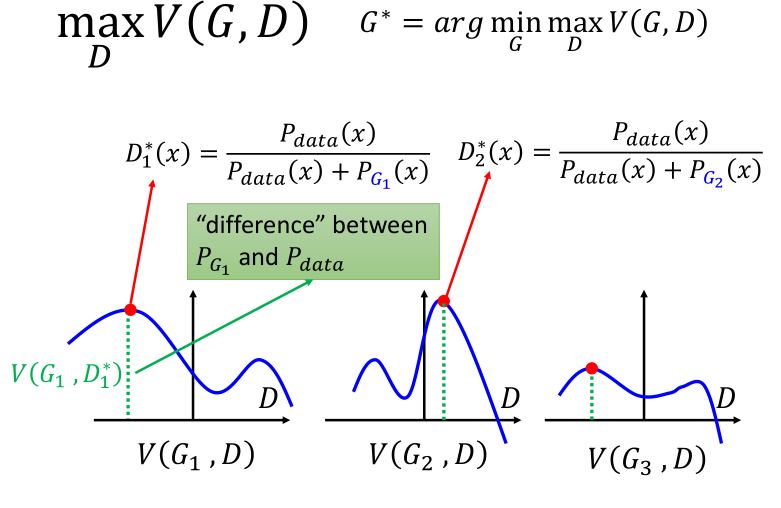
G最优解

同理，我们可以求$\underset{D}{max}\ V(G,D)$，我们将前面的得到的$D^{*}=\frac{P_{d a t a}(x)}{P_{d a t a}(x)+P_{G}(x)}$带入可得：

\[% <![CDATA[
\begin{align}
& \underset{D}{min}\ V(G,D) \\
& = V(G,D^{* })\\
& = E_{x \sim P_{data} } \left [\ log\ D^{* }(x) \ \right ] + E_{x \sim P_{G} } \left [\ log\ (1-D^{* }(x)) \ \right ] \\
& = E_{x \sim P_{data} } \left [\ log\ \frac{P_{data}(x)}{P_{data}(x)+P_G(x)} \ \right ] + E_{x \sim P_{G} } \left [\ log\ \frac{P_{G}(x)}{P_{data}(x)+P_G(x)} \ \right ]\\
& = \int_{x} P_{data}(x) log \frac{P_{data}(x)}{P_{data}(x)+P_G(x)} dx+ \int_{x} P_G(x)log(\frac{P_{G}(x)}{P_{data}(x)+P_G(x)})dx \\
& = \int_{x} P_{data}(x) log \frac{\frac{1}{2}P_{data}(x)}{\frac{P_{data}(x)+P_G(x)}{2} } dx+ \int_{x} P_{G}(x) log \frac{\frac{1}{2}P_{G}(x)}{\frac{P_{data}(x)+P_G(x)}{2} } dx \\
& = \int_{x}P_{data}(x)\left ( log \frac{1}{2}+log \frac{P_{data}(x)}{\frac{P_{data}(x)+P_G(x)}{2} } \right ) dx \\
& \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ + \int_{x}P_{G}(x)\left ( log \frac{1}{2}+log \frac{P_{G}(x)}{\frac{P_{data}(x)+P_G(x)}{2} } \right ) dx \\
& = \int_{x}P_{data}(x) log \frac{1}{2} dx + \int_{x}P_{data}(x) log \frac{P_{data}(x)}{\frac{P_{data}(x)+P_G(x)}{2} } dx \\
& \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ + \int_{x}P_{G}(x) log \frac{1}{2} dx + \int_{x}P_{G}(x) log \frac{P_{G}(x)}{\frac{P_{data}(x)+P_G(x)}{2} } dx \\
& = 2 log \frac{1}{2} + \int_{x}P_{data}(x) log \frac{P_{data}(x)}{\frac{P_{data}(x)+P_G(x)}{2} } dx + \int_{x}P_{G}(x) log \frac{P_{G}(x)}{\frac{P_{data}(x)+P_G(x)}{2} } dx\\
& = 2 log \frac{1}{2} + 2 \times \left [ \frac{1}{2} KL\left( P_{data}(x) || \frac{P_{data}(x)+P_{G}(x)}{2}\right )\right ] \\
& \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ + 2 \times \left [ \frac{1}{2} KL\left( P_{G}(x) || \frac{P_{data}(x)+P_{G}(x)}{2}\right )\right ] \\
& = -2 log 2 + 2 JSD \left ( P_{data}(x) || P_G(x) \right)
\end{align} %]]>
\]

其中$JSD ( P_{data}(x) || P_G(x))$的取值范围是从 $0$到$log2$，其中当$P_{data} = P_G$是，$JSD$取最小值0。也就是说$ V(G,D)$的取值范围是$0$到$-2log2$，也就是说$ V(G,D)$存在最小值，且此时$P_{data} = P_G$。

算法流程

上述我们从理论上讨论了全局最优值的可行性，但实际上样本空间是无穷大的，也就是我们没办法获得它的真实期望（$\mathbb{E}_{\boldsymbol{x} \sim p_{\text {data }}(\boldsymbol{x})}$和$\mathbb{E}_{\boldsymbol{z} \sim p_{\boldsymbol{z}}}(\boldsymbol{z})$是未知的），因此我们使用估测的方法来进行。

\[\tilde V = \frac{1}{m}\sum_{i=1}^{m} log D(x^i) + \frac{1}{m}\sum_{i=1}^{m} log (1-D(\tilde x^i))
\]

算法流程图如下所示（来自生成对抗网络——原理解释和数学推导）：

总结

上述便是GAN网络的数学原理，以及推导流程还有算法。我也是刚开始学，参考了如下的博客，其中生成对抗网络——原理解释和数学推导非常值得一看，里面非常详细的对GAN进行了推导，同时，bilibili——【机器学习】白板推导系列(三十一) ～生成对抗网络(GAN)中的视频也不错，手把手白板的对公式进行了推导。如有任何问题，或文章有任何错误，欢迎在评论区下方留言。

参考