机器学习（ML）八之正向传播、反向传播和计算图，及数值稳定性和模型初始化

正向传播

正向传播的计算图

通常绘制计算图来可视化运算符和变量在计算中的依赖关系。下图绘制了本节中样例模型正向传播的计算图，其中左下角是输入，右上角是输出。可以看到，图中箭头方向大多是向右和向上，其中方框代表变量，圆圈代表运算符，箭头表示从输入到输出之间的依赖关系。

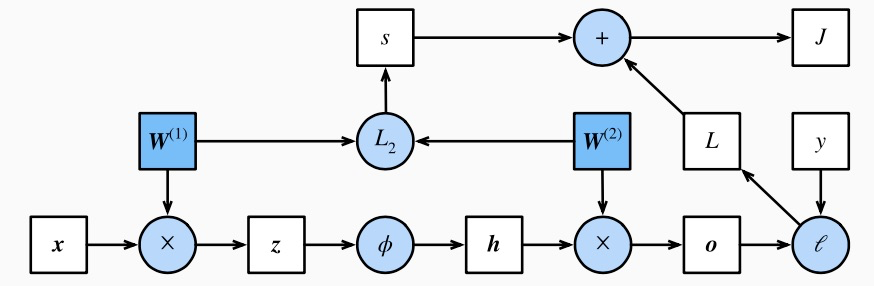
反向传播

训练深度学习模型

在训练深度学习模型时，正向传播和反向传播之间相互依赖。一方面，正向传播的计算可能依赖于模型参数的当前值，而这些模型参数是在反向传播的梯度计算后通过优化算法迭代的而这些当前值是优化算法最近一次根据反向传播算出梯度后迭代得到的。另一方面，反向传播的梯度计算可能依赖于各变量的当前值，而这些变量的当前值是通过正向传播计算得到的。这个当前值是通过从输入层到输出层的正向传播计算并存储得到的。因此，在模型参数初始化完成后，我们交替地进行正向传播和反向传播，并根据反向传播计算的梯度迭代模型参数。既然我们在反向传播中使用了正向传播中计算得到的中间变量来避免重复计算，那么这个复用也导致正向传播结束后不能立即释放中间变量内存。这也是训练要比预测占用更多内存的一个重要原因。另外需要指出的是，这些中间变量的个数大体上与网络层数线性相关，每个变量的大小跟批量大小和输入个数也是线性相关的，它们是导致较深的神经网络使用较大批量训练时更容易超内存的主要原因。

数值稳定性和模型初始化

理解了正向传播与反向传播以后，我们来讨论一下深度学习模型的数值稳定性问题以及模型参数的初始化方法。深度模型有关数值稳定性的典型问题是衰减（vanishing）和爆炸（explosion）。

衰减和爆炸

在神经网络中，通常需要随机初始化模型参数。下面我们来解释这样做的原因。

为了方便解释，假设输出层只保留一个输出单元o1（删去o2和o3以及指向它们的箭头），且隐藏层使用相同的激活函数。如果将每个隐藏单元的参数都初始化为相等的值，那么在正向传播时每个隐藏单元将根据相同的输入计算出相同的值，并传递至输出层。在反向传播中，每个隐藏单元的参数梯度值相等。因此，这些参数在使用基于梯度的优化算法迭代后值依然相等。之后的迭代也是如此。在这种情况下，无论隐藏单元有多少，隐藏层本质上只有1个隐藏单元在发挥作用。因此，正如在前面的实验中所做的那样，我们通常将神经网络的模型参数，特别是权重参数，进行随机初始化。

MXNet的默认随机初始化

随机初始化模型参数的方法有很多。在“机器学习（ML）一之 Linear Regression”一节中，我们使用net.initialize(init.Normal(sigma=0.01))使模型net的权重参数采用正态分布的随机初始化方式。如果不指定初始化方法，如net.initialize()，MXNet将使用默认的随机初始化方法：权重参数每个元素随机采样于-0.07到0.07之间的均匀分布，偏差参数全部清零。

Xavier随机初始化

还有一种比较常用的随机初始化方法叫作Xavier随机初始化。 假设某全连接层的输入个数为a，输出个数为b，Xavier随机初始化将使该层中权重参数的每个元素都随机采样于均匀分布

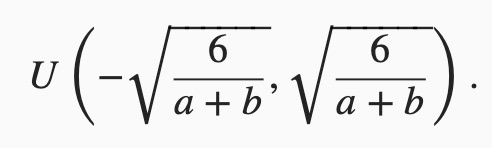
它的设计主要考虑到，模型参数初始化后，每层输出的方差不该受该层输入个数影响，且每层梯度的方差也不该受该层输出个数影响。

实战Kaggle比赛：房价预测代码实现

 #!/usr/bin/env python
 # coding: utf-8

 # In[1]:

 # 如果没有安装pandas，则反注释下面一行
 # !pip install pandas

 get_ipython().run_line_magic('matplotlib', 'inline')
 import d2lzh as d2l
 from mxnet import autograd, gluon, init, nd
 from mxnet.gluon import data as gdata, loss as gloss, nn
 import numpy as np
 import pandas as pd

 # In[2]:

 train_data = pd.read_csv('./data/kaggle_house_pred_train.csv')
 test_data = pd.read_csv('./data/kaggle_house_pred_test.csv')

 # In[3]:

 train_data.shape

 # In[4]:

 test_data.shape

 # In[5]:

 train_data.iloc[0:4, [0, 1, 2, 3, -3, -2, -1]]

 # In[6]:

 all_features = pd.concat((train_data.iloc[:, 1:-1], test_data.iloc[:, 1:]))

 # ### 预处理数据
 # 我们对连续数值的特征做标准化（standardization）：设该特征在整个数据集上的均值为μ，标准差为σ。那么，我们可以将该特征的每个值先减去μ再除以σ得到标准化后的每个特征值。对于缺失的特征值，我们将其替换成该特征的均值。

 # In[7]:

 numeric_features = all_features.dtypes[all_features.dtypes != 'object'].index
 all_features[numeric_features] = all_features[numeric_features].apply(
     lambda x: (x - x.mean()) / (x.std()))
 # 标准化后，每个特征的均值变为0，所以可以直接用0来替换缺失值
 all_features[numeric_features] = all_features[numeric_features].fillna(0)

 # 接下来将离散数值转成指示特征。举个例子，假设特征MSZoning里面有两个不同的离散值RL和RM，那么这一步转换将去掉MSZoning特征，并新加两个特征MSZoning_RL和MSZoning_RM，其值为0或1。如果一个样本原来在MSZoning里的值为RL，那么有MSZoning_RL=1且MSZoning_RM=0。

 # In[9]:

 # dummy_na=True将缺失值也当作合法的特征值并为其创建指示特征
 all_features = pd.get_dummies(all_features, dummy_na=True)
 all_features.shape

 # 可以看到这一步转换将特征数从79增加到了331。
 #
 # 最后，通过values属性得到NumPy格式的数据，并转成NDArray方便后面的训练。

 # In[10]:

 n_train = train_data.shape[0]
 train_features = nd.array(all_features[:n_train].values)
 test_features = nd.array(all_features[n_train:].values)
 train_labels = nd.array(train_data.SalePrice.values).reshape((-1, 1))

 # In[11]:

 loss = gloss.L2Loss()

 def get_net():
     net = nn.Sequential()
     net.add(nn.Dense(1))
     net.initialize()
     return net

 # 下面定义比赛用来评价模型的对数均方根误差。给定预测值$\hat y_1, \ldots, \hat y_n$和对应的真实标签$y_1,\ldots, y_n$，它的定义为
 #
 # $$\sqrt{\frac{1}{n}\sum_{i=1}^n\left(\log(y_i)-\log(\hat y_i)\right)^2}.$$
 #
 # 对数均方根误差的实现如下。

 # In[12]:

 def log_rmse(net, features, labels):
     # 将小于1的值设成1，使得取对数时数值更稳定
     clipped_preds = nd.clip(net(features), 1, float('inf'))
     rmse = nd.sqrt(2 * loss(clipped_preds.log(), labels.log()).mean())
     return rmse.asscalar()

 # In[13]:

 def train(net, train_features, train_labels, test_features, test_labels,
           num_epochs, learning_rate, weight_decay, batch_size):
     train_ls, test_ls = [], []
     train_iter = gdata.DataLoader(gdata.ArrayDataset(
         train_features, train_labels), batch_size, shuffle=True)
     # 这里使用了Adam优化算法
     trainer = gluon.Trainer(net.collect_params(), 'adam', {
         'learning_rate': learning_rate, 'wd': weight_decay})
     for epoch in range(num_epochs):
         for X, y in train_iter:
             with autograd.record():
                 l = loss(net(X), y)
             l.backward()
             trainer.step(batch_size)
         train_ls.append(log_rmse(net, train_features, train_labels))
         if test_labels is not None:
             test_ls.append(log_rmse(net, test_features, test_labels))
     return train_ls, test_ls

 # ### K 折交叉验证
 # 我们在“模型选择、欠拟合和过拟合”中介绍了K折交叉验证。它将被用来选择模型设计并调节超参数。下面实现了一个函数，它返回第i折交叉验证时所需要的训练和验证数据。

 # In[14]:

 def get_k_fold_data(k, i, X, y):
     assert k > 1
     fold_size = X.shape[0] // k
     X_train, y_train = None, None
     for j in range(k):
         idx = slice(j * fold_size, (j + 1) * fold_size)
         X_part, y_part = X[idx, :], y[idx]
         if j == i:
             X_valid, y_valid = X_part, y_part
         elif X_train is None:
             X_train, y_train = X_part, y_part
         else:
             X_train = nd.concat(X_train, X_part, dim=0)
             y_train = nd.concat(y_train, y_part, dim=0)
     return X_train, y_train, X_valid, y_valid

 # In[15]:

 #在 K 折交叉验证中我们训练 K 次并返回训练和验证的平均误差。
 def k_fold(k, X_train, y_train, num_epochs,
            learning_rate, weight_decay, batch_size):
     train_l_sum, valid_l_sum = 0, 0
     for i in range(k):
         data = get_k_fold_data(k, i, X_train, y_train)
         net = get_net()
         train_ls, valid_ls = train(net, *data, num_epochs, learning_rate,
                                    weight_decay, batch_size)
         train_l_sum += train_ls[-1]
         valid_l_sum += valid_ls[-1]
         if i == 0:
             d2l.semilogy(range(1, num_epochs + 1), train_ls, 'epochs', 'rmse',
                          range(1, num_epochs + 1), valid_ls,
                          ['train', 'valid'])
         print('fold %d, train rmse %f, valid rmse %f'
               % (i, train_ls[-1], valid_ls[-1]))
     return train_l_sum / k, valid_l_sum / k

 # In[16]:

 #模型选择----我们使用一组未经调优的超参数并计算交叉验证误差。可以改动这些超参数来尽可能减小平均测试误差。
 k, num_epochs, lr, weight_decay, batch_size = 5, 100, 5, 0, 64
 train_l, valid_l = k_fold(k, train_features, train_labels, num_epochs, lr,
                           weight_decay, batch_size)
 print('%d-fold validation: avg train rmse %f, avg valid rmse %f'
       % (k, train_l, valid_l))

 # In[17]:

 #预测并在Kaggle提交结果
 def train_and_pred(train_features, test_features, train_labels, test_data,
                    num_epochs, lr, weight_decay, batch_size):
     net = get_net()
     train_ls, _ = train(net, train_features, train_labels, None, None,
                         num_epochs, lr, weight_decay, batch_size)
     d2l.semilogy(range(1, num_epochs + 1), train_ls, 'epochs', 'rmse')
     print('train rmse %f' % train_ls[-1])
     preds = net(test_features).asnumpy()
     test_data['SalePrice'] = pd.Series(preds.reshape(1, -1)[0])
     submission = pd.concat([test_data['Id'], test_data['SalePrice']], axis=1)
     submission.to_csv('submission.csv', index=False)

 # In[18]:

 train_and_pred(train_features, test_features, train_labels, test_data,
                num_epochs, lr, weight_decay, batch_size)