Matlab实现K-Means聚类算法

人生如戏！！！！

一、理论准备

聚类算法，不是分类算法。分类算法是给一个数据，然后判断这个数据属于已分好的类中的具体哪一类。聚类算法是给一大堆原始数据，然后通过算法将其中具有相似特征的数据聚为一类。

K-Means算法的基本思想是初始随机给定K个簇中心，按照最邻近原则把待分类样本点分到各个簇。然后按平均法重新计算各个簇的质心，从而确定新的簇心。一直迭代，直到簇心的移动距离小于某个给定的值。

算法大致思路：
      1、从给定样本中任选几个点作为初始中心（我取k=2）
      2、计算其余点分别和初始中心点的距离，跟哪个初始中心近就跟那个中心点归为一类(欧式距离公式)，直到各自为“派别”
      3、在分好类的基础上按平均值的方法重新计算聚类中心点，再重复第二步...以此类推
      4、直到最后算法收敛（可以理解为中心点不再变动）则结束。

小知识点：

（1）s=size(A),
         当只有一个输出参数时，返回一个行向量，该行向量的第一个元素时矩阵的行数，第二个元素是矩阵的列数。
   （2）[r,c]=size(A),
         当有两个输出参数时，size函数将矩阵的行数返回到第一个输出变量r，将矩阵的列数返回到第二个输出变量c。
   （3）size(A,n)如果在size函数的输入参数中再添加一项n，并用1或2为n赋值，则 size将返回矩阵的行数或列数。其中r=size(A,1)该语句返回的时矩阵A的行数， c=size(A,2) 该语句返回的时矩阵A的列数。
另外，length()=max(size())。

二、算法实现

  1: %K-means算法主程序

  2: k=4;

  3: x =[ 1.2126   2.1338   0.5115   0.2044

  4:   -0.9316   0.7634   0.0125   -0.2752

  5:   -2.9593   0.1813   -0.8833   0.8505

  6:   3.1104   -2.5393   -0.0588   0.1808

  7:   -3.1141   -0.1244   -0.6811   0.9891

  8:   -3.2008   0.0024   -1.2901   0.9748

  9:   -1.0777   1.1438   0.1996   0.0139

 10:   -2.7213   -0.1909   0.1184   0.1013

 11:   -1.1467   1.3820   0.1427   -0.2239

 12:   1.1497   1.9414   -0.3035   0.3464

 13:   2.6993   -2.2556   0.1637   -0.0139

 14:   -3.0311   0.1417   0.0888   0.1791

 15:   -2.8403   -0.1809   -0.0965   0.0817

 16:   1.0118   2.0372   0.1638   -0.0349

 17:   -0.8968   1.0260   -0.1013   0.2369

 18:   1.1112   1.8802   -0.0291   -0.1506

 19:   1.1907   2.2041   -0.1060   0.2167

 20:   -1.0114   0.8029   -0.1317   0.0153

 21:   -3.1715   0.1041   -0.3338   0.0321

 22:   0.9718   1.9634   0.0305   -0.3259

 23:   -1.0377   0.8889   -0.2834   0.2301

 24:   -0.8989   1.0185   -0.0289   0.0213

 25:   -2.9815   -0.4798   0.2245   0.3085

 26:   -0.8576   0.9231   -0.2752   -0.0091

 27:   -3.1356   0.0026   -1.2138   0.7733

 28:   3.4470   -2.2418   0.2014   -0.1556

 29:   2.9143   -1.7951   0.1992   -0.2146

 30:   3.4961   -2.4969   -0.0121   0.1315

 31:   -2.9341   -0.1071   -0.7712   0.8911

 32:   -2.8105   -0.0884   -0.0287   -0.1279

 33:   3.1006   -2.0677   -0.2002   -0.1303

 34:   0.8209   2.1724   0.1548   0.3516

 35:   -2.8500   0.3196   0.1359   -0.1179

 36:   -2.8679   0.1365   -0.5702   0.7626

 37:   -2.8245   -0.1312   0.0881   -0.1305

 38:   -0.8322   1.3014   -0.3837   0.2400

 39:   -2.6063   0.1431   0.1880   0.0487

 40:   -3.1341   -0.0854   -0.0359   -0.2080

 41:   0.6893   2.0854   -0.3250   -0.1007

 42:   1.0894   1.7271   -0.0176   0.6553

 43:   -2.9851   -0.0113   0.0666   -0.0802

 44:   1.0371   2.2724   0.1044   0.3982

 45:   -2.8032   -0.2737   -0.7391   1.0277

 46:   -2.6856   0.0619   -1.1066   1.0485

 47:   -2.9445   -0.1602   -0.0019   0.0093

 48:   1.2004   2.1302   -0.1650   0.3413

 49:   3.2505   -1.9279   0.4462   -0.2405

 50:   -1.2080   0.8222   0.1671   0.1576

 51:   -2.8274   0.1515   -0.9636   1.0675

 52:   2.8190   -1.8626   0.2702   0.0026

 53:   1.0507   1.7776   -0.1421   0.0999

 54:   -2.8946   0.1446   -0.1645   0.3071

 55:   -1.0105   1.0973   0.0241   0.1628

 56:   -2.9138   -0.3404   0.0627   0.1286

 57:   -3.0646   -0.0008   0.3819   -0.1541

 58:   1.2531   1.9830   -0.0774   0.2413

 59:   1.1486   2.0440   -0.0582   -0.0650

 60:   -3.1401   -0.1447   -0.6580   0.9562

 61:   -2.9591   0.1598   -0.6581   1.1937

 62:   -2.9219   -0.3637   -0.1538   -0.2085

 63:   2.8948   -2.2745   0.2332   -0.0312

 64:   -3.2972   -0.0219   -0.0288   -0.1436

 65:   -1.2737   0.7648   0.0643   0.0858

 66:   -1.0690   0.8108   -0.2723   0.3231

 67:   -0.5908   0.7508   -0.5456   0.0190

 68:   0.5808   2.0573   -0.1658   0.1709

 69:   2.8227   -2.2461   0.2255   -0.3684

 70:   0.6174   1.7654   -0.3999   0.4125

 71:   3.2587   -1.9310   0.2021   0.0800

 72:   1.0999   1.8852   -0.0475   -0.0585

 73:   -2.7395   0.2585   -0.8441   0.9987

 74:   -1.2223   1.0542   -0.2480   -0.2795

 75:   -2.9212   -0.0605   -0.0259   0.2591

 76:   3.1598   -2.2631   0.1746   0.1485

 77:   0.8476   1.8760   -0.2894   -0.0354

 78:   2.9205   -2.2418   0.4137   -0.2499

 79:   2.7656   -2.1768   0.0719   -0.1848

 80:   -0.8698   1.0249   -0.2084   -0.0008

 81:   -1.1444   0.7787   -0.4958   0.3676

 82:   -1.0711   1.0450   -0.0477   -0.4030

 83:   0.5350   1.8110   -0.0377   0.1622

 84:   0.9076   1.8845   -0.1121   0.5700

 85:   -2.7887   -0.2119   0.0566   0.0120

 86:   -1.2567   0.9274   0.1104   0.1581

 87:   -2.9946   -0.2086   -0.8169   0.6662

 88:   1.0536   1.9818   -0.0631   0.2581

 89:   -2.8465   -0.2222   0.2745   0.1997

 90:   -2.8516   0.1649   -0.7566   0.8616

 91:   -3.2470   0.0770   0.1173   -0.1092

 92:   -2.9322   -0.0631   -0.0062   -0.0511

 93:   -2.7919   0.0438   -0.1935   -0.5023

 94:   0.9894   1.9475   -0.0146   -0.0390

 95:   -2.9659   -0.1300   0.1144   0.3410

 96:   -2.7322   -0.0427   -1.0758   0.9718

 97:   -1.4852   0.8592   -0.0503   -0.1373

 98:   2.8845   -2.1465   -0.0533   -0.1044

 99:   -3.1470   0.0536   0.1073   0.3323

100:   2.9423   -2.1572   0.0505   0.1180

101:   -3.0683   0.3434   -0.6563   0.8960

102:   1.3215   2.0951   -0.1557   0.3994

103:   -0.7681   1.2075   -0.2781   0.2372

104:   -0.6964   1.2360   -0.3342   0.1662

105:   -0.6382   0.8204   -0.2587   0.3344

106:   -3.0233   -0.1496   -0.2607   -0.0400

107:   -0.8952   0.9872   0.0019   0.3138

108:   -0.8172   0.6814   -0.0691   0.1009

109:   -3.3032   0.0571   -0.0243   -0.1405

110:   0.7810   1.9013   -0.3996   0.7374

111:   -0.9030   0.8646   -0.1498   0.1112

112:   -0.8461   0.9261   -0.1295   -0.0727

113:   2.8182   -2.0818   -0.1430   -0.0547

114:   2.9295   -2.3846   -0.0244   -0.1400

115:   1.0587   2.2227   -0.1250   0.0957

116:   3.0755   -1.7365   -0.0511   0.1500

117:   -1.3076   0.8791   -0.3720   0.0331

118:   -2.8252   -0.0366   -0.6790   0.7374

119:   -2.6551   -0.1875   0.3222   0.0483

120:   -2.9659   -0.1585   0.4013   -0.1402

121:   -3.2859   -0.1546   0.0104   -0.1781

122:   -0.6679   1.1999   0.1396   -0.3195

123:   -1.0205   1.2226   0.1850   0.0050

124:   -3.0091   -0.0186   -0.9111   0.9663

125:   -3.0339   0.1377   -0.9662   1.0664

126:   0.8952   1.9594   -0.3221   0.3579

127:   -2.8481   0.1963   -0.1428   0.0382

128:   1.0796   2.1353   -0.0792   0.6491

129:   -0.8732   0.8985   -0.0049   0.0068

130:   1.0620   2.1478   -0.1275   0.3553

131:   3.4509   -1.9975   0.1285   -0.1575

132:   -3.2280   -0.0640   -1.1513   0.8235

133:   -0.6654   0.9402   0.0577   -0.0175

134:   -3.2100   0.2762   -0.1053   0.0626

135:   3.0793   -2.0043   0.2948   0.0411

136:   1.3596   1.9481   -0.0167   0.3958

137:   -3.1267   0.1801   0.2228   0.1179

138:   -0.7979   0.9892   -0.2673   0.4734

139:   2.5580   -1.7623   -0.1049   -0.0521

140:   -0.9172   1.0621   -0.0826   0.1501

141:   -0.7817   1.1658   0.1922   0.0803

142:   3.1747   -2.1442   0.1472   -0.3411

143:   2.8476   -1.8056   -0.0680   0.1536

144:   -0.6175   1.4349   -0.1970   -0.1085

145:   0.7308   1.9656   0.2602   0.2801

146:   -1.0310   1.0553   -0.2928   -0.1647

147:   -2.9251   -0.2095   0.0582   -0.1813

148:   -0.9827   1.2720   -0.2225   0.2563

149:   -1.0830   1.1158   -0.0405   -0.1181

150:   -2.8744   0.0195   -0.3811   0.1455

151:   3.1663   -1.9241   0.0455   0.1684

152:   -1.0734   0.7681   -0.4725   -0.1976];

153: [n,d] = size(x);

154: bn=round(n/k*rand);%第一个随机数在前1/K的范围内

155: %；表示按列显示，都好表示按行显示

156: nc=[x(bn,:);x(2*bn,:);x(3*bn,:);x(4*bn,:)];%初始聚类中心

157: %x(bn,:) 选择某一行数据作为聚类中心，其列值为全部

158:

159: %x数据源，k聚类数目，nc表示k个初始化聚类中心

160: %cid表示每个数据属于哪一类，nr表示每一类的个数，centers表示聚类中心

161: [cid,nr,centers] = kmeans(x,k,nc)%调用kmeans函数

162: %认为不该是150，或者说不该是个确定值，该是size(x,1)就是x行数

163: for i=1:150

164:   if cid(i)==1,

165:      plot(x(i,1),x(i,2),'r*') % 显示第一类

166:     %plot(x(i,2),'r*') % 显示第一类

167:     hold on

168:   else

169:       if cid(i)==2,

170:         plot(x(i,1),x(i,2),'b*') %显示第二类

171:         %  plot(x(i,2),'b*') % 显示第一类

172:           hold on

173:       else

174:               if cid(i)==3,

175:                     plot(x(i,1),x(i,2),'g*') %显示第三类

176:                    % plot(x(i,2),'g*') % 显示第一类

177:                     hold on

178:                   else

179:                       if cid(i)==4,

180:                        plot(x(i,1),x(i,2),'k*') %显示第四类

181:                         % plot(x(i,2),'k*') % 显示第一类

182:                         hold on

183:                       end

184:               end

185:         end

186:   end

187: end

188: strt=['红色*为第一类；蓝色*为第二类；绿色*为第三类；黑色*为第四类' ];

189: text(-4,-3.6,strt); 

  1: %BasicKMeans.m主类

  2: %x数据源，k聚类数目，nc表示k个初始化聚类中心

  3: %cid表示每个数据属于哪一类，nr表示每一类的个数，centers表示聚类中心

  4: function [cid,nr,centers] = kmeans(x,k,nc)

  5:     [n,d] = size(x);

  6:     % 设置cid为分类结果显示矩阵

  7:     cid = zeros(1,n);

  8:     % Make this different to get the loop started.

  9:     oldcid = ones(1,n);

 10:     % The number in each cluster.

 11:     nr = zeros(1,k);

 12:     % Set up maximum number of iterations.

 13:     maxgn= 100;

 14:     iter = 1;

 15:     %计算每个数据到聚类中心的距离 ,选择最小的值得位置到cid

 16:     %我记得是聚类中心近乎不再变化迭代停止

 17:     while iter < maxgn

 18:         for i = 1:n

 19:             %repmat 即 Replicate Matrix ，复制和平铺矩阵，是 MATLAB 里面的一个函数。

 20:             %B = repmat(A,m,n)将矩阵 A 复制 m×n 块，即把 A 作为 B 的元素，B 由 m×n 个 A 平铺而成。B 的维数是 [size(A,1)*m, size(A,2)*n] 。

 21:             %点乘方a.^b,矩阵a中每个元素按b中对应元素乘方或者b是常数

 22:             %sum(x,2)表示矩阵x的横向相加，求每行的和，结果是列向量。 而缺省的sum(x)就是竖向相加，求每列的和，结果是行向量。

 23:             dist = sum((repmat(x(i,:),k,1)-nc).^2,2);

 24:             [m,ind] = min(dist); % 将当前聚类结果存入cid中

 25:             cid(i) = ind;

 26:         end

 27:          %找到每一类的所有数据，计算他们的平均值，作为下次计算的聚类中心

 28:         for i = 1:k

 29:             %find（A>m,4）返回矩阵A中前四个数值大于m的元素所在位置

 30:             ind = find(cid==i);

 31:             %mean(a,1)=mean(a)纵向;mean(a,2)横向

 32:             nc(i,:) = mean(x(ind,:));

 33:             %统计每一类的数据个数

 34:             nr(i) = length(ind);

 35:         end

 36:         iter = iter + 1;

 37:     end

 38:

 39:     % Now check each observation to see if the error can be minimized some more.

 40:     % Loop through all points.

 41:

 42:     maxiter = 2;

 43:     iter = 1;

 44:     move = 1;

 45:     %j~=k这是一个逻辑表达式，j不等于k，如果j不等于k，返回值为1，否则为0

 46:     while iter < maxiter & move ~= 0

 47:         move = 0;

 48:         %对所有的数据进行再次判断，寻求最佳聚类结果

 49:         for i = 1:n

 50:             dist = sum((repmat(x(i,:),k,1)-nc).^2,2);

 51:             r = cid(i); % 将当前数据属于的类给r

 52:             %点除，a.\b表示矩阵b的每个元素除以a中对应元素或者除以常数a，a./b表示常数a除以矩阵b中每个元素或者矩阵a除以矩阵b对应元素或者常数b

 53:             %nr是没一类的的个数

 54:

 55:

 56:

 57:             %这个调整看不懂

 58:             %点乘(对应元素相乘),必须同维或者其中一个是标量，a.*b

 59:             dadj = nr./(nr+1).*dist'; % 计算调整后的距离

 60:

 61:             [m,ind] = min(dadj); % 找到该数据距哪个聚类中心最近

 62:             if ind ~= r % 如果不等则聚类中心移动

 63:                   cid(i) = ind;%将新的聚类结果送给cid

 64:                   ic = find(cid == ind);%重新计算调整当前类别的聚类中心

 65:                   nc(ind,:) = mean(x(ic,:));

 66:                   move = 1;

 67:             end

 68:         end

 69:         iter = iter+1;

 70:     end

 71:     centers = nc;

 72:     if move == 0

 73:         disp('No points were moved after the initial clustering procedure.')

 74:     else

 75:         disp('Some points were moved after the initial clustering procedure.')

 76:     end

三、算法结果

控制台自动输出的结果如下，我很奇怪怎么自己输出了。

  1: >> main

  2: No points were moved after the initial clustering procedure.

  3: cid =

  4:   Columns 1 through 22

  5:      2     3     1     4     1     1     3     1     3     2     4     1     1     2     3     2     2     3     1     2     3     3

  6:   Columns 23 through 44

  7:      1     3     1     4     4     4     1     1     4     2     1     1     1     3     1     1     2     2     1     2     1     1

  8:   Columns 45 through 66

  9:      1     2     4     3     1     4     2     1     3     1     1     2     2     1     1     1     4     1     3     3     3     2

 10:   Columns 67 through 88

 11:      4     2     4     2     1     3     1     4     2     4     4     3     3     3     2     2     1     3     1     2     1     1

 12:   Columns 89 through 110

 13:      1     1     1     2     1     1     3     4     1     4     1     2     3     3     3     1     3     3     1     2     3     3

 14:   Columns 111 through 132

 15:      4     4     2     4     3     1     1     1     1     3     3     1     1     2     1     2     3     2     4     1     3     1

 16:   Columns 133 through 150

 17:      4     2     1     3     4     3     3     4     4     3     2     3     1     3     3     1     4     3

 18: nr =

 19:     55    30    40    25

 20: centers =

 21:   -2.962918181818183  -0.023009090909091  -0.297021818181818   0.341136363636364

 22:    0.995233333333333   1.997873333333334  -0.078486666666667   0.229650000000000

 23:   -0.956882500000000   0.997800000000000  -0.123667500000000   0.049320000000000

 24:    3.023444000000000  -2.098592000000001   0.102096000000000  -0.050580000000000

每次运行结果得到的图片都不一样，最奇怪的是第二个图片竟然重叠类别。

   

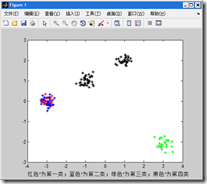
四、结果分析

不适合处理离散型属性，但是对于连续型具有较好的聚类效果。

对于不同的初始值，可能会导致不同结果：多设置一些不同的初值，但比较耗时和浪费资源。

分类数目K不确定：通过类的自动合并和分裂，得到较为合理的类型数目K，例如ISODATA算法。相同点：聚类中心都是通过样本均值的迭代运算来决定的；不同点：主要是在选代过程中可将一类一分为二，亦可能二类合二为一，即“自组织”，这种算法具有启发式的特点。由于算法有自我调整的能力，因而需要设置若干个控制用参数，如聚类数期望值K、最小类内样本数、类间中心距离参数、每次迭代允许合并的最大聚类对数L及允许迭代次数I等。

参考了老王的课件。