bzoj1227 [SDOI2009]虔诚的墓主人(组合公式+离散化+线段树)

1227: [SDOI2009]虔诚的墓主人

Time Limit: 5 Sec Memory Limit: 259 MB
Submit: 803 Solved: 372
[Submit][Status][Discuss]

Description

小W 是一片新造公墓的管理人。公墓可以看成一块N×M 的矩形，矩形的每个格点，要么种着一棵常青树，要么是一块还没有归属的墓地。当地的居民都是非常虔诚的基督徒，他们愿意提前为自己找一块合适墓地。为了体现自己对主的真诚，他们希望自己的墓地拥有着较高的虔诚度。一块墓地的虔诚度是指以这块墓地为中心的十字架的数目。一个十字架可以看成中间是墓地，墓地的正上、正下、正左、正右都有恰好k 棵常青树。小W 希望知道他所管理的这片公墓中所有墓地的虔诚度总和是多少

Input

第一行包含两个用空格分隔的正整数N 和M，表示公墓的宽和长，因此这个矩形公墓共有(N+1) ×(M+1)个格点，左下角的坐标为(0, 0)，右上角的坐标为(N, M)。第二行包含一个正整数W，表示公墓中常青树的个数。第三行起共W 行，每行包含两个用空格分隔的非负整数xi和yi，表示一棵常青树的坐标。输入保证没有两棵常青树拥有相同的坐标。最后一行包含一个正整数k，意义如题目所示。

Output

包含一个非负整数，表示这片公墓中所有墓地的虔诚度总和。为了方便起见，答案对2,147,483,648 取模。

Sample Input

5 6
13
0 2
0 3
1 2
1 3
2 0
2 1
2 4
2 5
2 6
3 2
3 3
4 3
5 2
2

Sample Output

HINT

图中，以墓地(2, 2)和(2, 3)为中心的十字架各有3个，即它们的虔诚度均为3。其他墓地的虔诚度为0。对于30%的数据，满足1 ≤ N, M ≤ 1,000。对于60%的数据，满足1 ≤ N, M ≤ 1,000,000。对于100%的数据，满足1 ≤ N, M ≤ 1,000,000,000，0 ≤ xi ≤ N，0 ≤ yi ≤ M，1 ≤ W ≤ 100,000， 1 ≤ k ≤ 10。存在50%的数据，满足1 ≤ k ≤ 2。存在25%的数据，满足1 ≤ W ≤ 10000。

【思路】

组合公式+离散化+区间查询&单点修改。

　　　如果设每一个空格左右上下各有的树之数目为left[][],right[][],up[][],down[][]，则答案为

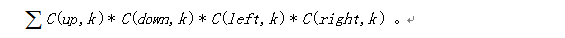
　　　考虑到nm很大，这里我们先进行离散化，离散化之后时间复杂度为O(ww)。

考虑y同的两棵相邻的树（中间为空格）且x分别为ab，我们统计夹在中间的空格的分数，则为

前两项相同，因此只需要统计ab区间内的C之积即可，可以用线段树在O(logn)的时间内完成。

具体操作：

　　　　依次扫描每一棵树：

　　如果与前一棵树同y则累计答案。

　　维护cy表示当前y扫描过的树之数目。

　　维护cx[]表示x被扫描过的树之数目。

　　　维护线段树。　

需要注意的是n在线段树中定义为离散后x的最大下标。

【代码】

 #include<cstdio>

 #include<cstring>

 #include<iostream>

 #include<algorithm>

 #define FOR(a,b,c) for(int a=(b);a<=(c);a++)

 using namespace std;

 typedef long long LL;

 const int maxn = +;

 const LL MOD = 2147483648LL;

 struct Node{

     int x,y;

     bool operator<(const Node& rhs) const{

         return y<rhs.y || (y==rhs.y && x<rhs.x);

     }

 }nodes[maxn];

 int read() {

     char c=getchar();

     while(!isdigit(c)) c=getchar();

     int x=;

     while(isdigit(c)) {

         x=x*+c-'';

         c=getchar();

     }

     return x;

 }

 //线段树相关

 //+单点修改+区间求和

 LL sumv[*maxn];

 int v; LL d;

 void update(int u,int L,int R) {

     int lc=u*,rc=lc+;

     if(L==R) {

         sumv[u]=d;

     }

     else {

         int M=L+(R-L)/;

         if(v<=M) update(lc,L,M);

         else update(rc,M+,R);

         sumv[u]=sumv[lc]+sumv[rc];

     }

 }

 int y1,y2;

 LL query(int u,int L,int R) {

     int lc=u*,rc=lc+;

     if(y1<=L && R<=y2) {

         return sumv[u];

     }

     else {

         int M=L+(R-L)/;

         LL res=;

         if(y1<=M) res += query(lc,L,M);

         if(M<y2)  res += query(rc,M+,R);

         res %= MOD;

         return res;

     }

 }

 //组合函数相关

 LL C[maxn][];

 void get_C(int n) {

     C[][]=;

     for(int i=;i<=n;i++) {

         C[i][]=C[i][i]=;

         for(int j=;j<=;j++)

             C[i][j]=(C[i-][j]+C[i-][j-])%MOD;

     }

 }

 int cx[maxn],sumx[maxn],sumy[maxn];

 int hash[*maxn],x[maxn],y[maxn];

 int n,m,w,k;

 int main() {

     n=read(),m=read(),w=read();

     get_C(w);

     int p=;

     FOR(i,,w) {

         x[i]=read(),y[i]=read();

         hash[p++]=x[i],hash[p++]=y[i];

     }

     p--;

     k=read();

     //离散化坐标

     sort(hash+,hash+p+);

     p=unique(hash+,hash+p+)-hash; p--;

     n=;

     FOR(i,,w) {

         x[i]=lower_bound(hash+,hash+p+,x[i])-hash;

         y[i]=lower_bound(hash+,hash+p+,y[i])-hash;

         n=max(n,x[i]);                                     //n用于线段树表示最大x下标

         sumx[x[i]]++,sumy[y[i]]++;

         nodes[i]=(Node){x[i],y[i]};

     }

     sort(nodes+,nodes+w+);

     //扫描每一棵树

     LL ans=,cy=;

     FOR(i,,w) {

         int r=nodes[i].x,c=nodes[i].y;

         if(i> && c==nodes[i-].y) {

             y1=nodes[i-].x+,y2=nodes[i].x-;

             if(y1<=y2) ans = (ans+C[cy][k]*C[sumy[c]-cy][k]%MOD*query(,,n)%MOD)%MOD;

             cy++;

         }

         else cy=;

         cx[r]++;

         v=r; d=C[cx[r]][k]*C[sumx[r]-cx[r]][k]%MOD;

         update(,,n);

     }

     printf("%lld\n",ans);

     return ;

 }