bzoj 2803 [POI2012]prefixuffix hsh+性质

题目大意

bzoj 2803

对于两个串S1、S2，如果能够将S1的一个后缀移动到开头后变成S2，就称S1和S2循环相同。例如串ababba和串abbaab是循环相同的。

给出一个长度为n的串S，求满足下面条件的最大的L：

1. \(L\le \frac n 2\)
2. S的L前缀和S的L后缀是循环相同的。

\(n\le 1,000,000\)

分析

题意相当于找一段前缀=后缀（1）

删掉这两段后再找一段前缀=后缀（2）

长度和就是答案了

其中(1)部分随便搞\(O(n)\) \(hsh\)扫过去就好了

为了复习写了发\(kmp\)

(2)部分有一个神性质，可以\(dp\)

记\(f[i]\)表示不跨越\(mid\)的情况下，以\(i\)开头的前缀和以\(n-i+1\)结束的后缀的最大匹配长度

重要性质：$$f[i-1]<=f[i]+2$$

证明：

令\(j=n-i+1\)

设f[i]对应的最长匹配为\([i,A]\) 与 \([B,j]\) （3）

\(f[i-1]\le f[i]+2\)

就是如图



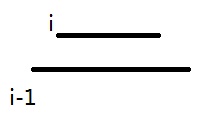
原式相当于\(i-1\)的匹配位置不超过原来匹配位置的下一位

反证一波：

设匹配到第A+K(K>=2)位

则\([i-1~,~A+K]=[B-K~,~j+1]\)

取这两段的第二位到倒数第二位

有\([i,A+K-1]=[B-(K-1)~,~j]\)

与（3）矛盾

注意

此题神数据卡hash

于是我开了双hash继续Wa

3hash就过了

所以感觉双hsh姿势应该是

一个自然溢出，一个取模，可能效果更好

kmp姿势

本文kmp姿势错误，切勿学习

solution

#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <cctype>
#include <cmath>
#include <algorithm>
using namespace std;
typedef unsigned long long ull;
typedef long long LL;
const int Q=1000000007;
const int M=1000007;
const ull W=131;
const ull X=1313;
const LL Z=13131;

int n;
char s[M];
int f[M];
int nxt[M];
ull hsh1[M],pw1[M];
ull hsh2[M],pw2[M];
LL hsh3[M],pw3[M];

void kmp(){
	nxt[1]=0;
	int i,k=0;
	for(i=1;i<=n;i++){
		while(k&&s[k]!=s[i]) k=nxt[k];
		nxt[i+1]=++k;
	}
}

ull gethsh1(int x,int y){
	return hsh1[y]-hsh1[x-1]*pw1[y-x+1];
}

ull gethsh2(int x,int y){
	return hsh2[y]-hsh2[x-1]*pw2[y-x+1];
}

LL gethsh3(int x,int y){
	return ((hsh3[y]-hsh3[x-1]*pw3[y-x+1]%Q)%Q+Q)%Q;
}

int main(){
	int i;
	scanf("%d",&n);
	scanf("%s",s+1);
	for(pw1[0]=1,i=1;i<=n;i++) pw1[i]=pw1[i-1]*W;
	for(pw2[0]=1,i=1;i<=n;i++) pw2[i]=pw2[i-1]*X;
	for(pw3[0]=1,i=1;i<=n;i++) pw3[i]=pw3[i-1]*Z%Q;
	for(i=1;i<=n;i++) hsh1[i]=hsh1[i-1]*W+s[i];
	for(i=1;i<=n;i++) hsh2[i]=hsh2[i-1]*X+s[i];
	for(i=1;i<=n;i++) hsh3[i]=(hsh3[i-1]*Z+s[i])%Q;

	f[n/2+1]=0;
	for(i=n/2;i;i--){
		f[i]=f[i+1]+2;
		while(f[i]&&i+f[i]-1>n/2) f[i]--;
		while(f[i]&&(gethsh1(i,i+f[i]-1)!=gethsh1(n-i+1-f[i]+1,n-i+1)
			||gethsh2(i,i+f[i]-1)!=gethsh2(n-i+1-f[i]+1,n-i+1))
			||gethsh3(i,i+f[i]-1)!=gethsh3(n-i+1-f[i]+1,n-i+1)) f[i]--;
	}
	kmp();
	int ans=0;
	for(i=nxt[n+1];i;i=nxt[i])
		if(i<=n/2) ans=max(ans,(i-1)+f[i]);

	printf("%d\n",ans);
	return 0;
}